haar
首先说一下一维haar小波的原理。
例如我们有一个一维的图像[2,4,6,8,10,12,14,16].
- 求均值:我们求相邻像素的均值[3,7,11,15]。这个新的图像分辨率就成了原来的一半(8/2=4)。
-
求差值。上面的均值我们存储了图像的整体信息。但是很多细节信息我们丢掉了,所以我们同时要记录图像的细节信息,这样在重构时能够恢复图像的全部信息。下面是求第m个差值的公式:
b[m]=(a[2m]−a[2m+1])/2
经过计算我们得到了结果[-1,-1,-1,-1]。这个新的分辨率也成了原来的一半(8/2=4)。
3. 此时上面两步形成了第一次分解的结果[3,7,11,15,-1,-1,-1,-1]。包含了图像的整体信息和细节信息。接下来的分解我们重复1,2步,将整体信息再次进行分解,得到了二级分解结果[5,13,-2,-2].同样的,前面的[5,13]是整体信息,后面的[-2,-2]是细节信息。
| 分辨率 | 整体信息 | 细节信息 |
|---|---|---|
| 4 | 3,7,11,15 | -1,-1,-1,-1 |
| 2 | 5,13 | -2,-2 |
| 1 | 9 | -4 |
经过三次分解,我们得到了一个整体信息和三个细节系数,这个就是一维小波变换。
对于二维haar小波,我们通常一次分解形成了整体图像,水平细节,垂直细节,对角细节。首先我们按照一维haar小波分解的原理,按照行顺序对行进行处理,然后按照列顺序对行处理结果进行同样的处理。最后形成了如下的形式。
一、Haar小波的基本原理
数学理论方面的东西我也不是很熟悉,这边主要用简单的例子来介绍下Haar小波的使用情况。
例如:有a=[8,7,6,9]四个数,并使用b[4]数组来保存结果.
则一级Haar小波变换的结果为:
b[0]=(a[0]+a[1])/2, b[2]=(a[0]-a[1])/2
b[1]=(a[2]+a[3])/2, b[3]=(a[2]-a[3])/2
即依次从数组中取两个数字,计算它们的和以及差,并将和一半和差的一半依次保存在数组的前半部分和后半部分。
例如:有a[8],要进行一维Haar小波变换,结果保存在b[8]中
则一级Haar小波变换的结果为:
b[0]=(a[0]+a[1])/2, b[4]=(a[0]-a[1])/2
b[1]=(a[2]+a[3])/2, b[5]=(a[2]-a[3])/2
b[2]=(a[4]+a[5])/2, b[6]=(a[4-a[5]])/2
b[3]=(a[6]+a[7])/2, b[7]=(a[6]-a[7])/2
如果需要进行二级Haar小波变换的时候,只需要对b[0]-b[3]进行Haar小波变换.
对于二维的矩阵来讲,每一级Haar小波变换需要先后进行水平方向和竖直方向上的两次一维小波变换,行和列的先后次序对结果不影响。
(1)图像/矩阵进行Haar小波的基本原理
首先我们简单了解一下二维小波变换的塔式结构。我们知道,一维小波变换其实是将一维原始信号分别经过低通滤波和高通滤波以及二元下抽样得到信号的低频部分L和高频部分H。而根据Mallat算法,二维小波变换可以用一系列的一维小波变换得到。对一幅m行n列的图像,二维小波变换的过程是先对图像的每一行做一维小波变换,得到L和H两个对半部分;然后对得到的LH图像(仍是m行n列)的每一列做一维小波变换。这样经过一级小波变换后的图像就可以分为LL,HL,LH,HH四个部分,如下图所示,就是一级二维小波变换的塔式结构:

而二级、三级以至更高级的二维小波变换则是对上一级小波变换后图像的左上角部分(LL部分)再进行一级二维小波变换,是一个递归过程。下图是三级二维小波变换的塔式结构图:

一个图像经过小波分解后,可以得到一系列不同分辨率的子图像,不同分辨率的子图像对应的频率也不同。高分辨率(即高频)子图像上大部分点的数值都接近于0,分辨率越高,这种现象越明显。要注意的是,在N级二维小波分解中,分解级别越高的子图像,频率越低。例如图2的三级塔式结构中,子图像HL2、LH2、HH2的频率要比子图像HL1、LH1、HH1的频率低,相应地分辨率也较低。
【
题外:haar特征为什么叫haar的一个可能原因
大嘴查了查各种资料,基本没有说清楚,最接近的一种解释如下(大嘴整理了下一段,此段是合并了几种解释):
“Haar特征因为类似于Haar小波而得名,Haar-likefeatures提取过程可看作对图像局部进行Haar小波变换,它反映了图像局部的灰度变化,当然不是直接进行变换,而通常是以一种简便的方式如积分图像。通常作目标检测/识别也不会是对图像整体进行Haar小波变换,而是将图像密集化为一些小块,在每个小块上做变换。对图像整体进行Haar小波变换分析系数当然也可做些边缘检测等工作。Haar型特征的计算是通过积分图像实现的”
看完这段后想想haar的其中一个特征(对角特征):

是不是和前面介绍的塔型结构比较像,莫非这就是所谓的类似haar小波?哈,有知道准确答案的朋友告诉大嘴一下。
】
(2)用一行数据进行Haar小波的基本原理
这边主要用简单的例子来介绍下Haar小波的使用情况。例如:有a=[8,7,6,9]四个数,并使用b[4]数组来保存结果.则一级Haar小波变换的结果为:
b[0]=(a[0] a[1])/2,
b[1]=(a[2] a[3])/2,
b[2]=(a[0]-a[1])/2
b[3]=(a[2]-a[3])/2
即依次从数组中取两个数字,计算它们的和以及差,并将和一半和差的一半依次保存在数组的前半部分和后半部分。
例如:有a[8],要进行一维Haar小波变换,结果保存在b[8]中,则一级Haar小波变换的结果为:
b[0]=(a[0] a[1])/2,
b[1]=(a[2] a[3])/2,
b[2]=(a[4] a[5])/2,
b[3]=(a[6] a[7])/2,
b[4]=(a[0]-a[1])/2,
b[5]=(a[2]-a[3])/2,
b[6]=(a[4-a[5]])/2,
b[7]=(a[6]-a[7])/2,
如果需要进行二级Haar小波变换的时候,只需要对b[0]~b[3]进行Haar小波变换.
对于二维的矩阵来讲,每一级Haar小波变换需要先后进行水平方向和竖直方向上的两次一维小波变换,行和列的先后次序对结果不影响。
通过以上变换,大家可以知道,小波变换是可逆的,即完全可以从b[0]~b[7]反向求出a[0]~a[7]
提供函数DWT()和IDWT(),前者完成任意层次的小波变换,后者完成任意层次的小波逆变换。输入 图像要求必须是单通道浮点图像,对图像大小也有要求(1层变换:w,h必须是2的倍数;2层变换:w,h必须是4的倍数;3层变换:w,h必须是8的倍数......),变换后的结果直接保存在输入图像中。1、 函数参数简单,图像指针pImage和变换层数nLayer。
2、一个函数直接完成多层次二维小波变换,尽量减少下标运算,避免不必要的函数调用,以提高执行效率。
3、变换过程中,使用了一个指针数组pData用于保存每行数据的起始位置,pRow和pColumn用于保存一行和一列临时数据,用于奇偶分离或合并,内存消耗较少。
- 代码: 全选
-
// 二维离散小波变换(单通道浮点图像)
void DWT(IplImage *pImage, int nLayer)
{
// 执行条件
if (pImage)
{
if (pImage->nChannels == 1 &&
pImage->depth == IPL_DEPTH_32F &&
((pImage->width >> nLayer) << nLayer) == pImage->width &&
((pImage->height >> nLayer) << nLayer) == pImage->height)
{
int i, x, y, n;
float fValue = 0;
float fRadius = sqrt(2.0f);
int nWidth = pImage->width;
int nHeight = pImage->height;
int nHalfW = nWidth / 2;
int nHalfH = nHeight / 2;
float **pData = new float*[pImage->height];
float *pRow = new float[pImage->width];
float *pColumn = new float[pImage->height];
for (i = 0; i < pImage->height; i++)
{
pData[i] = (float*) (pImage->imageData + pImage->widthStep * i);
}
// 多层小波变换
for (n = 0; n < nLayer; n++, nWidth /= 2, nHeight /= 2, nHalfW /= 2, nHalfH /= 2)
{
// 水平变换
for (y = 0; y < nHeight; y++)
{
// 奇偶分离
memcpy(pRow, pData[y], sizeof(float) * nWidth);
for (i = 0; i < nHalfW; i++)
{
x = i * 2;
pData[y][i] = pRow[x];
pData[y][nHalfW + i] = pRow[x + 1];
}
// 提升小波变换
for (i = 0; i < nHalfW - 1; i++)
{
fValue = (pData[y][i] + pData[y][i + 1]) / 2;
pData[y][nHalfW + i] -= fValue;
}
fValue = (pData[y][nHalfW - 1] + pData[y][nHalfW - 2]) / 2;
pData[y][nWidth - 1] -= fValue;
fValue = (pData[y][nHalfW] + pData[y][nHalfW + 1]) / 4;
pData[y][0] += fValue;
for (i = 1; i < nHalfW; i++)
{
fValue = (pData[y][nHalfW + i] + pData[y][nHalfW + i - 1]) / 4;
pData[y][i] += fValue;
}
// 频带系数
for (i = 0; i < nHalfW; i++)
{
pData[y][i] *= fRadius;
pData[y][nHalfW + i] /= fRadius;
}
}
// 垂直变换
for (x = 0; x < nWidth; x++)
{
// 奇偶分离
for (i = 0; i < nHalfH; i++)
{
y = i * 2;
pColumn[i] = pData[y][x];
pColumn[nHalfH + i] = pData[y + 1][x];
}
for (i = 0; i < nHeight; i++)
{
pData[i][x] = pColumn[i];
}
// 提升小波变换
for (i = 0; i < nHalfH - 1; i++)
{
fValue = (pData[i][x] + pData[i + 1][x]) / 2;
pData[nHalfH + i][x] -= fValue;
}
fValue = (pData[nHalfH - 1][x] + pData[nHalfH - 2][x]) / 2;
pData[nHeight - 1][x] -= fValue;
fValue = (pData[nHalfH][x] + pData[nHalfH + 1][x]) / 4;
pData[0][x] += fValue;
for (i = 1; i < nHalfH; i++)
{
fValue = (pData[nHalfH + i][x] + pData[nHalfH + i - 1][x]) / 4;
pData[i][x] += fValue;
}
// 频带系数
for (i = 0; i < nHalfH; i++)
{
pData[i][x] *= fRadius;
pData[nHalfH + i][x] /= fRadius;
}
}
}
delete[] pData;
delete[] pRow;
delete[] pColumn;
}
}
}
// 二维离散小波恢复(单通道浮点图像)
void IDWT(IplImage *pImage, int nLayer)
{
// 执行条件
if (pImage)
{
if (pImage->nChannels == 1 &&
pImage->depth == IPL_DEPTH_32F &&
((pImage->width >> nLayer) << nLayer) == pImage->width &&
((pImage->height >> nLayer) << nLayer) == pImage->height)
{
int i, x, y, n;
float fValue = 0;
float fRadius = sqrt(2.0f);
int nWidth = pImage->width >> (nLayer - 1);
int nHeight = pImage->height >> (nLayer - 1);
int nHalfW = nWidth / 2;
int nHalfH = nHeight / 2;
float **pData = new float*[pImage->height];
float *pRow = new float[pImage->width];
float *pColumn = new float[pImage->height];
for (i = 0; i < pImage->height; i++)
{
pData[i] = (float*) (pImage->imageData + pImage->widthStep * i);
}
// 多层小波恢复
for (n = 0; n < nLayer; n++, nWidth *= 2, nHeight *= 2, nHalfW *= 2, nHalfH *= 2)
{
// 垂直恢复
for (x = 0; x < nWidth; x++)
{
// 频带系数
for (i = 0; i < nHalfH; i++)
{
pData[i][x] /= fRadius;
pData[nHalfH + i][x] *= fRadius;
}
// 提升小波恢复
fValue = (pData[nHalfH][x] + pData[nHalfH + 1][x]) / 4;
pData[0][x] -= fValue;
for (i = 1; i < nHalfH; i++)
{
fValue = (pData[nHalfH + i][x] + pData[nHalfH + i - 1][x]) / 4;
pData[i][x] -= fValue;
}
for (i = 0; i < nHalfH - 1; i++)
{
fValue = (pData[i][x] + pData[i + 1][x]) / 2;
pData[nHalfH + i][x] += fValue;
}
fValue = (pData[nHalfH - 1][x] + pData[nHalfH - 2][x]) / 2;
pData[nHeight - 1][x] += fValue;
// 奇偶合并
for (i = 0; i < nHalfH; i++)
{
y = i * 2;
pColumn[y] = pData[i][x];
pColumn[y + 1] = pData[nHalfH + i][x];
}
for (i = 0; i < nHeight; i++)
{
pData[i][x] = pColumn[i];
}
}
// 水平恢复
for (y = 0; y < nHeight; y++)
{
// 频带系数
for (i = 0; i < nHalfW; i++)
{
pData[y][i] /= fRadius;
pData[y][nHalfW + i] *= fRadius;
}
// 提升小波恢复
fValue = (pData[y][nHalfW] + pData[y][nHalfW + 1]) / 4;
pData[y][0] -= fValue;
for (i = 1; i < nHalfW; i++)
{
fValue = (pData[y][nHalfW + i] + pData[y][nHalfW + i - 1]) / 4;
pData[y][i] -= fValue;
}
for (i = 0; i < nHalfW - 1; i++)
{
fValue = (pData[y][i] + pData[y][i + 1]) / 2;
pData[y][nHalfW + i] += fValue;
}
fValue = (pData[y][nHalfW - 1] + pData[y][nHalfW - 2]) / 2;
pData[y][nWidth - 1] += fValue;
// 奇偶合并
for (i = 0; i < nHalfW; i++)
{
x = i * 2;
pRow[x] = pData[y][i];
pRow[x + 1] = pData[y][nHalfW + i];
}
memcpy(pData[y], pRow, sizeof(float) * nWidth);
}
}
delete[] pData;
delete[] pRow;
delete[] pColumn;
}
}
}
原理:
A=[ a(1,1) a(1,2) a(1,3) a(1,4) …… a(1,n)
a(2,1) a(2,2) ……
a(3,1) a(3,2) ……
……
a(m,1) a(m,2) …… a(m,n) ]
已知有二维数据A,其中A是一个m*n的矩阵,现在我们需要将A进行Haar小波分解。
1、因为一维小波分解的序列个数为偶数个,仿造Matlab的思想,假如A的行数m为奇数,则将A矩阵的行数增加1,这时A的第m+1行的数据和第m行的数据一一对应(相等);类似的,如果A矩阵的列数n为奇数,则将A矩阵的列数增加1,这时A的第n+1列的数据和第n列的数据一一对应(相等)
2、常规的分解算法是先将A矩阵的每一行(列)作为单独的序列进行一维Harr小波分解,然后再将,然后再对分解的数组再进行列(行)小波分解,最后得到想要的结果.因为Haar小波的特殊性,本文不这样进行分解,而是对行与列同时进行Harr小波分解,这就是本文与一般的Haar小波分解不同的地方。看代码吧!
函数:
1、Haar小波分解
WaveletTransformHaar(x,LL,LH,HL,HH)
x:需要进行Harr小波分解的二维数组
LL:小波分解得到的低低位值
LH:小波分解得到的低高位值
HL:小波分解得到的高低位值
HH:小波分解得到的高高位值
2、Haar小波重构
WaveletTransformHaar_Inv(LL,LH,HL,HH)
LL:之前小波分解得到的低低位值
LH:之前小波分解得到的低高位值
HL:之前小波分解得到的高低位值
HH:之前小波分解得到的高高位值
执行完毕返回重构的x数据
例子:
A =
[ 8.00000000000000 37.0000000000000 37.0000000000000 1.00000000000000
21.0000000000000 49.0000000000000 21.0000000000000 32.0000000000000
2.00000000000000 39.0000000000000 7.00000000000000 14.0000000000000
34.0000000000000 24.0000000000000 20.0000000000000 44.0000000000000
9.00000000000000 6.00000000000000 43.0000000000000 5.00000000000000
12.0000000000000 39.0000000000000 18.0000000000000 14.0000000000000 ]
WaveletTransformHaar(A,LL,LH,HL,HH)//执行命令后得到如下结果
LL =
[ 57.5000000000000 45.5000000000000
49.5000000000000 42.5000000000000
33.0000000000000 40.0000000000000 ]
LH =
[-12.5000000000000 -7.50000000000000
-8.50000000000000 -21.5000000000000
-18.0000000000000 8.00000000000000 ]
HL =
[-28.5000000000000 12.5000000000000
-13.5000000000000 -15.5000000000000
-12.0000000000000 21.0000000000000 ]
HH =
[-0.50000000000000 23.5000000000000
-23.5000000000000 8.50000000000000
15.0000000000000 17.0000000000000 ]
B=WaveletTransformHaar_Inv(LL,LH,HL,HH)//执行命令后得到如下结果,可以发现和A是一样的
B =
[ 8.00000000000000 37.0000000000000 37.0000000000000 1.00000000000000
21.0000000000000 49.0000000000000 21.0000000000000 32.0000000000000
2.00000000000000 39.0000000000000 7.00000000000000 14.0000000000000
34.0000000000000 24.0000000000000 20.0000000000000 44.0000000000000
9.00000000000000 6.00000000000000 43.0000000000000 5.00000000000000
12.0000000000000 39.0000000000000 18.0000000000000 14.0000000000000 ]
SIFT/SURF、haar特征、广义hough变换的特性对比分析
SIFT/SURF基于灰度图,
一、首先建立图像金字塔,形成三维的图像空间,通过Hessian矩阵获取每一层的局部极大值,然后进行在极值点周围26个点进行NMS,从而得到粗略的特征点,再使用二次插值法得到精确特征点所在的层(尺度),即完成了尺度不变。
二、在特征点选取一个与尺度相应的邻域,求出主方向,其中SIFT采用在一个正方形邻域内统计所有点的梯度方向,找到占80%以上的方向作为主方向;而SURF则选择圆形邻域,并且使用活动扇形的方法求出特征点主方向,以主方向对齐即完成旋转不变。
三、以主方向为轴可以在每个特征点建立坐标,SIFT在特征点选择一块大小与尺度相应的方形区域,分成16块,统计每一块沿着八个方向占的比例,于是特征点形成了128维特征向量,对图像进行归一化则完成强度不变;而SURF分成64块,统计每一块的dx,dy,|dx|,|dy|的累积和,同样形成128维向量,再进行归一化则完成了对比度不变与强度不变。
haar特征也是基于灰度图,
首先通过大量的具有比较明显的haar特征(矩形)的物体图像用模式识别的方法训练出分类器,分类器是个级联的,每级都以大概相同的识别率保留进入下一级的具有物体特征的候选物体,而每一级的子分类器则由许多haar特征构成(由积分图像计算得到,并保存下位置),有水平的、竖直的、倾斜的,并且每个特征带一个阈值和两个分支值,每级子分类器带一个总的阈值。识别物体的时候,同样计算积分图像为后面计算haar特征做准备,然后采用与训练的时候有物体的窗口同样大小的窗口遍历整幅图像,以后逐渐放大窗口,同样做遍历搜索物体;每当窗口移动到一个位置,即计算该窗口内的haar特征,加权后与分类器中haar特征的阈值比较从而选择左或者右分支值,累加一个级的分支值与相应级的阈值比较,大于该阈值才可以通过进入下一轮筛选。当通过分类器所有级的时候说明这个物体以大概率被识别。
广义hough变换同样基于灰度图,
使用轮廓作为特征,融合了梯度信息,以投票的方式识别物体,在本blog的另一篇文章中有详细讨论,这里不再赘述。
特点异同对比及其适用场合:
三种算法都只是基于强度(灰度)信息,都是特征方法,但SIFT/SURF的特征是一种具有强烈方向性及亮度性的特征,这使得它适用于刚性形变,稍有透视形变的场合;haar特征识别方法带有一点人工智能的意味,对于像人脸这种有明显的、稳定结构的haar特征的物体最适用,只要结构相对固定即使发生扭曲等非线性形变依然可识别;广义hough变换完全是精确的匹配,可得到物体的位置方向等参数信息。前两种方法基本都是通过先获取局部特征然后再逐个匹配,只是局部特征的计算方法不同,SIFT/SURF比较复杂也相对稳定,haar方法比较简单,偏向一种统计的方法形成特征,这也使其具有一定的模糊弹性;广义hough变换则是一种全局的特征——轮廓梯度,但也可以看做整个轮廓的每一个点的位置和梯度都是特征,每个点都对识别有贡献,用直观的投票,看票数多少去确定是否识别出物体。
关于人脸检测中的Haar特征提取
AdaBoost人脸检测训练算法速度很重要的两方面是特征选取和特征计算。选取的特征为矩特征为Haar特征,计算的方法为积分图。
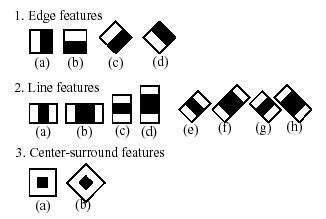
(1)Haar特征:
Haar特征分为三类:边缘特征、线性特征、中心特征和对角线特征,组合成特征模板。特征模板内有白色和黑色两种矩形,并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。在确定了特征形式后 Harr- like特征的数量就取决于训练样本图像矩阵的大小,特征模板在子窗口内任意放置,一种形态称为一种特征,找出所有子窗口的特征是进行弱分类训练的基础。
(2)积分图:
积分图(Integral Image)主要的思想是将图像从起点开始到各个点所形成的矩形区域像素之和作为一个数组的元素保存在内存中,当要计算某个区域的像素和时可以直接索引数组的元素,不用重新计算这个区域的像素和,从而加快了计算。“积分图"能够在多种尺度下,使用相同的时间来计算不同的特征,因此大大提高了检测速度。
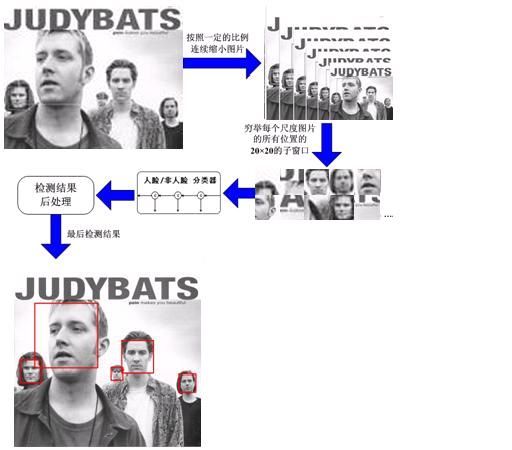
目标检测方法最初由Paul Viola [Viola01]提出,并由Rainer Lienhart [Lienhart02]对这一方法进行了改善.首先,利用样本(大约几百幅样本图片)的 harr特征进行分类器训练,得到一个级联的boosted分类器。训练样本分为正例样本和反例样本,其中正例样本是指待检目标样本(例如人脸或汽车等),反例样本指其它任意图片,所有的样本图片都被归一化为同样的尺寸大小(例如,20x20)。
分类器训练完以后,就可以应用于输入图像中的感兴趣区域(与训练样本相同的尺寸)的检测。检测到目标区域(汽车或人脸)分类器输出为1,否则输出为0。为了检测整副图像,可以在图像中移动搜索窗口,检测每一个位置来确定可能的目标。为了搜索不同大小的目标物体,分类器被设计为可以进行尺寸改变,这样比改变待检图像的尺寸大小更为有效。所以,为了在图像中检测未知大小的目标物体,扫描程序通常需要用不同比例大小的搜索窗口对图片进行几次扫描。
分类器中的“级联”是指最终的分类器是由几个简单分类器级联组成。在图像检测中,被检窗口依次通过每一级分类器,这样在前面几层的检测中大部分的候选区域就被排除了,全部通过每一级分类器检测的区域即为目标区域。目前支持这种分类器的boosting技术有四种: Discrete Adaboost, Real Adaboost, Gentle Adaboostand Logitboost。"boosted"即指级联分类器的每一层都可以从中选取一个boosting算法(权重投票),并利用基础分类器的自我训练得到。基础分类器是至少有两个叶结点的决策树分类器。 Haar特征是基础分类器的输入,主要描述如下。目前的算法主要利用下面的Harr特征。
每个特定分类器所使用的特征用形状、感兴趣区域中的位置以及比例系数(这里的比例系数跟检测时候采用的比例系数是不一样的,尽管最后会取两个系数的乘积值)来定义。例如在第三行特征(2c)的情况下,响应计算为复盖全部特征整个矩形框(包括两个白色矩形框和一个黑色矩形框)象素的和减去黑色矩形框内象素和的三倍。每个矩形框内的象素和都可以通过积分图象很快的计算出来。(察看下面和对cvIntegral的描述).通过HaarFaceDetect 的演示版可以察看目标检测的工作情况。
AdaBoost人脸检测原理
对人脸检测的研究最初可以追溯到 20 世纪 70 年代,早期的研究主要致力于模板匹配、子空间方法,变形模板匹配等。近期人脸检测的研究主要集中在基于数据驱动的学习方法,如统计模型方法,神经网络学习方法,统计知识理论和支持向量机方法,基于马尔可夫随机域的方法,以及基于肤色的人脸检测。目前在实际中应用的人脸检测方法多为基于Adaboost学习算法的方法。
Viola人脸检测方法是一种基于积分图、级联检测器和AdaBoost算法的方法,方法框架可以分为以下三大部分:
第一部分,使用Harr-like特征表示人脸,使用“积分图”实现特征数值的快速计算;
第二部分,使用Adaboost算法挑选出一些最能代表人脸的矩形特征(弱分类器),按照加权投票的方式将弱分类器构造为一个强分类器;
第三部分,将训练得到的若干强分类器串联组成一个级联结构的层叠分类器,级联结构能有效地提高分类器的检测速度。
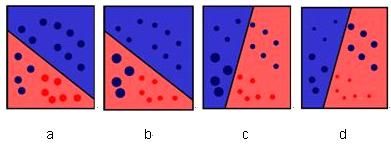
Adaboost算法是一种用来分类的方法,它的基本原理就是“三个臭皮匠,顶个诸葛亮”。它把一些比较弱的分类方法合在一起,组合出新的很强的分类方法。
例如下图中
需要用一些线段把红色的球与深蓝色的球分开,然而如果仅仅画一条线的话,是分不开的。
人脸检测的目的就是从图片中找出所有包含人脸的子窗口,将人脸的子窗口与非人脸的子窗口分开。
大致步骤如下:
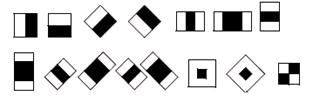
(1)在一个 20*20的图片提取一些简单的特征(称为Harr特征),如下图所示。
它的计算方法就是将白色区域内的像素和减去黑色区域,因此在人脸与非人脸图片的相同位置上,值的大小是不一样的,这些特征可以用来区分人脸和非人脸。
(2)目前的方法是使用数千张切割好的人脸图片,和上万张背景图片作为训练样本。训练图片一般归一化到20*20的大小。在这样大小的图片中,可供使用的 haar特征数在 1 万个左右,然后通过机器学习算法 —adaboost算法挑选数千个有效的 haar 特征来组成人脸检测器。
(3)学习算法训练出一个人脸检测器后,便可以在各个场合使用了。使用时,将图像按比例依次缩放,然后在缩放后的图片的 20*20的子窗口依次判别是人脸还是非人脸。
人脸检测的流程
人脸检测在实际中主要用于人脸识别的预处理,即在图像中准确标定出人脸的位置和大小。
目前人脸检测技术在门禁系统、智能监控系统中已得到了很好的应用。另外,目前的笔记本电脑中也陆续开始使用人脸识别技术作为计算机登录的凭证。近年来,在数码相机和手机中也集成了人脸检测算法,作为一个新的功能提供用户使用。在这些应用中,人脸检测都是发挥着至关重要的作用
Haar-like特征,即很多人常说的Haar特征,是计算机视觉领域一种常用的特征描述算子。它最早是由Papageorigiou等人用于人脸描述。目前常用的Haar-like特征可以分为三类:线性特征、边缘特征、点特征(中心特征)、对角线特征。如下图所示:
![]()
显然,边缘特征有4种:x方向,y方向,x倾斜方向,y倾斜方向;线特征有8种,点特征有2种,对角线特征有1种。每一种特征的计算都是由黑色填充区域的像素值之和与白色填充区域的像素值之和的差值。而计算出来的这个差值就是所谓的Haar-like特征的特征值。