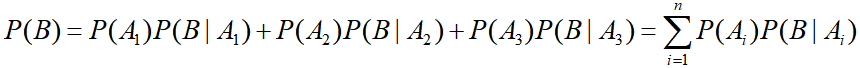机器学习之朴素贝叶斯（一）思想及典型例题手写实现

条件概率、全概率公式、贝叶斯公式

• 条件概率公式：

  在事件B发生的条件下，A发生的概率

  
  换一种写法：
  

  理解了条件概率公式后，用一个引例介绍后面两个公式：村子里有三个小偷，事件B={村子失窃}，已知小偷们的偷窃成功率依次是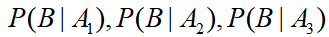，除夕夜去偷的概率依次是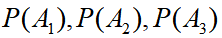

• 全概率公式：

  求：村庄除夕夜失窃的概率
  　　

• 贝叶斯公式：

  求：在村子失窃的条件下，偷窃者是某个小偷的概率
  

朴素贝叶斯

李航《统计学习方法》中的定义
朴素贝叶斯(naive Bayes) 法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。

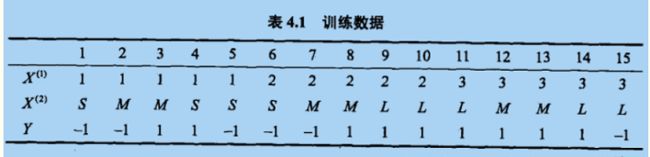
经典例题数据如下

X1,X2,Y
1,S,-1
1,M,-1
1,M,1
1,S,1
1,S,-1
2,S,-1
2,M,-1
2,M,1
2,L,1
2,L,1
3,L,1
3,M,1
3,M,1
3,L,1
3,L,-1
>>预测x1 = 2,x2 = 'S' 的类别

题目分析如下

1. 朴素贝叶斯最后输出的结果是多个概率的比较，输出最大的那个概率所对应的y值
2. 朴素贝叶斯是贝叶斯的变形
3. 去除了贝叶斯的分母，也就是全概率的计算和使用，使公式得到简化。
4. 朴素贝叶斯并不是准确的概率，只是近似比，但是这并不影响每个朴素贝叶斯的大小的比较
5. 在朴素贝叶斯中，影响最终结果的条件，是相互独立的。
6. 有几个条件对结果由影响，就是这几个条件的连乘
7. 本题中对预测结果造成影响的条件有两个，x1=2和x2=‘S’，那么可以理解为：
   P1(y=1|(x1=1,x2=‘S’)) = P(y=1) * P(x1=2|y=1) * P(x2=‘S’|y=1)
   P2(y=-1|(x1=1,x2=‘S’)) = P(y=-1) * P(x1=2|y=-1) * P(x2=‘S’|y=-1)
   最终将p1和p2进行比较，谁的值大，就分为那一类。
8. 剩下的事情就是统计计算需要的先验概率
9. P(y=1) = 9/16
   P(x1=2|y=1) = 3/6
   ……等等

代码实现如下

'''
    朴素贝叶斯
'''
import pandas as pd
df = pd.read_csv(r'../datas/bayes_lihang.txt',delimiter=',')
X = df.iloc[:,:-1]
y = df.iloc[:,-1]
y = list(set(y.values)) # 【1，-1】

# 预测数据
X_predict = [2,'S']
x1 = X_predict[0]
x2 = X_predict[1]

# 记录概率值和概率值所对应的y标签
dis = []
for df_y in y:
    # 1.统计标签为df_y的所有数据
    df_y_count =df[df['Y']==df_y]['Y'].count()
    # 2.统计所有样本的个数
    m = df.shape[0]
    # 3.统计df_y中，所有x1的数据个数
    x1_y = df[(df['Y']==df_y) & (df['X1']==x1)]['X1'].count()
    # 4.统计df_y中，所有x2的数据的个数
    x2_y = df[(df['Y']==df_y) & (df['X2']==x2)]['X2'].count()
    # 计算概率
    p = (df_y_count/m) * (x1_y/df_y_count) * (x2_y/df_y_count)
    # 存储概率 方便稍后比较
    dis.append([p,df_y])

# 排序 按照概率最大排序，输出第一个概率下的y标签
dis.sort(key=lambda s:s[0],reverse=True)
print(dis[0][1])