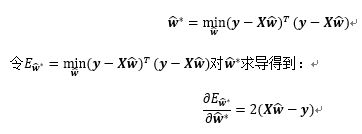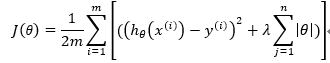线性回归、岭回归、lasso回归、弹性网络回归算法，附带python实现
线性回归
算法简介
线性回归，就是利用数理统计中的回归分析，来确定两种或两种以上变量间，相互依赖的定量关系的一种统计分析方法。
线性回归试图学得：
求解w和b的关键在于衡量f(xi)与yi之间的差别.由于均方误差是回归任务中最常用的性能度量，因此可以试图让均方误差最小化：
求解它可以利用最小二乘法和梯度下降方法等：
最小二乘法：
对于多元回归，我们一般吧w和b一起写成向量形式：w=(w;b)
,相应的吧数据集D表示为一个m×(d+1)
大小的矩阵X
因此最小化均方误差的公式可写为：
令上式为零可以得到
最优解的闭式解，当
为满秩矩阵或正定矩阵时，令上式为零可得：
然而，现实任务中
往往不是满秩矩阵，这里后面岭回归算法引入正则化可以用来进行求解。
而在现实任务中我们往往使用梯度下降一类的方法去拟合局部最优值（也是凸函数的全局最优值）来进行快速求解。
线性回归优点：
- 建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快。
- 可以根据系数给出每个变量的理解和解释
缺点：
- 对异常值很敏感
算法sklearn实现
这里直接循环训练十个数据集，并将结果保存在logis_scores数组中。
Sklearn中的线性回归是用的最小二乘法去拟合，需要调整的参数比较少，默认
Fit_intercept = False（是否存在截距）normalize = False(是否标准化)
算法手动实现
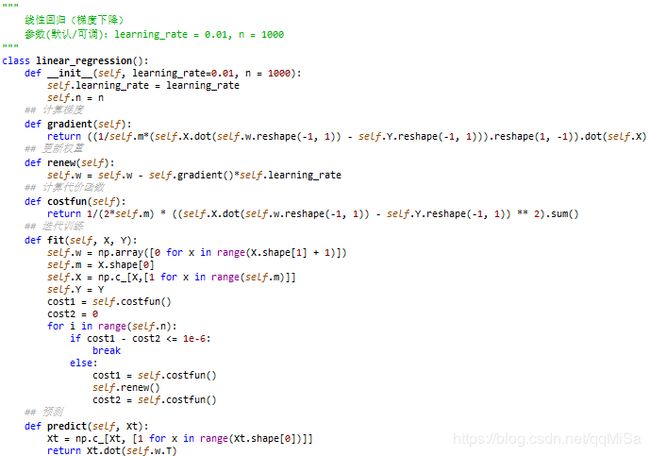
这里实现了采用梯度下降方法的线性回归
将自己实现的与sklearn提供的线性回归在十个数据集上做了对比
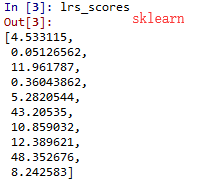
结果如下(评价指标MSE)：
有几个预测结果差异较大的原因是因为sklearn里面提供的是最小二乘法，而自己实现的采用的梯度下降法，而数据量较小，可以看到在数据量比较大的几个数据集中，两者相差并不多。
文中代码和数据集可在这里()下载。
岭回归
算法简介
岭回归在线性回归的基础上，增加了一个L2正则项，使得损失函数变为（令前面的
）：
其中λ
是我们手动给的一个正则系数.由于正则项的引入不仅使得回归可以直接通过最小二乘法求解，而且不仅仅如此，对角矩阵其实是由一个参数lamda和单位对角矩阵相乘组成。lamda越大，说明偏差就越大，原始数据对回归求取参数的作用就越小，当lamda取到一个合适的值，就能在一定意义上解决过拟合的问题：原先过拟合的特别大或者特别小的参数会被约束到正常甚至很小的值，但不会为零。
岭回归优点：
能在一定意义上解决过拟合的问题
缺点：
它缩小了系数的值，但没有达到零，这表明没有特征选择功能
sklearn实现
这里直接循环训练十个数据集，并将结果保存在ridge_scores数组中。
Sklearn中的岭回归默认L2正则系数为1（alpha = 1）
手动实现
这里类似于线性回归，因为当正则项系数为0时，岭回归就变成了线性回归。
默认正则项系数为1，与sklearn提供的岭回归在十个数据集上进行对比，结果如下：
文中代码和数据集可在这里()下载。
Lasso回归
算法简介
Lasso回归与岭回归的模型的不同仅仅在于它使用的是L1正则。但是模型带来的变化还是比较大的。它的损失函数为：
由于引入L1正则，所以损失函数不再能进行求导，也就是说，最小二乘法，梯度下降，牛顿迭代在这里都不能用了。针对这种情况可以使用坐标轴下降的方法进行求解。
Lasso回归优点：
Lasso方法可以达到变量选择的效果，将不显著的变量系数压缩至0
缺点：
会剔除某些对结果影响比较小但是比较重要的特征
sklearn实现
这里直接循环训练十个数据集，并将结果保存在lasso_scores数组中。
Sklearn中的Lasso回归默认L1正则系数为1（alpha = 1）
手动实现
由于L1正则无法进行求导，所以这里不能直接使用梯度下降进行求解，这里使用了坐标轴下降方法。
坐标轴下降方法的数学依据是：
对于一个可微凸函数
，其中
为
的向量，如果对于一个解
，使得在某个坐标轴上
都能达到最小值，则就是的全局的最小值点。
对应于Data1的训练模型，查看自己实现的Lasso回归训练出的系数
可以看到有三项被算法认为作用不大的特征权重被置零了。
比较自己实现的套索回归和sklearn库提供的回归：
文中代码和数据集可在这里()下载。
ElasticNet回归
算法简介
ElasticNet 是一种使用L1和L2先验作为正则化矩阵的线性回归模型.这种组合用于只有很少的权重非零的稀疏模型，比如Lasso, 但是又能保持Ridge 的正则化属性.我们可以使用 l1_ratio 参数来调节L1和L2的凸组合。当多个特征和另一个特征相关的时候弹性网络非常有用。Lasso 倾向于随机选择其中一个，而弹性网络更倾向于选择两个.在实践中，Lasso 和 Ridge 之间权衡的一个优势是它允许在循环过程中继承 Ridge 的稳定性.
ElasticNet优点：
既能像Lasso回归删除无效特征，又能继承岭回归的稳定性
缺点:
没有一个选择参数的规则，调参比较佛系.
sklearn实现
这里直接循环训练十个数据集，并将结果保存在elasticNet_scores数组中。
Sklearn里面默认α = 0.5（l1_ratio = 0.5），ρ = 1（alpha = 1）
手动实现
由于L1正则无法求导，所以这里也采用了坐标轴下降的方法
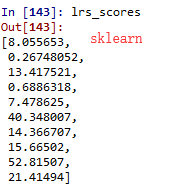
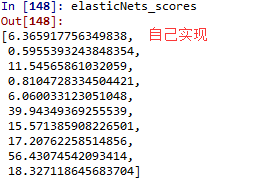
比较自己实现的ElasticNet回归和sklearn库提供的
文中代码和数据集可在这里()下载。