- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
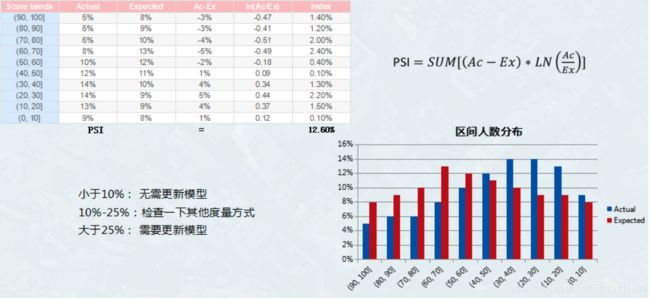
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- element实现动态路由+面包屑
软件技术NINI
vue案例vue.js前端
el-breadcrumb是ElementUI组件库中的一个面包屑导航组件,它用于显示当前页面的路径,帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中,如果你已经安装了ElementUI,就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例:安装ElementUI(如果你还没有安装的话):你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
- 理解Gunicorn:Python WSGI服务器的基石
范范0825
ipythonlinux运维
理解Gunicorn:PythonWSGI服务器的基石介绍Gunicorn,全称GreenUnicorn,是一个为PythonWSGI(WebServerGatewayInterface)应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具,Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置,帮助初学者快速上手。1.什么是Gunico
- swagger访问路径
igotyback
swagger
Swagger2.x版本访问地址:http://{ip}:{port}/{context-path}/swagger-ui.html{ip}是你的服务器IP地址。{port}是你的应用服务端口,通常为8080。{context-path}是你的应用上下文路径,如果应用部署在根路径下,则为空。Swagger3.x版本对于Swagger3.x版本(也称为OpenAPI3)访问地址:http://{ip
- 店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码
说私域
人工智能小程序
摘要:本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合,阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇,提升了用户信任感、拓展了营销渠道,并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展,社区团购作为一种新兴的商业模式,在满足消费者日常需
- 腾讯云技术深度探索:构建高效云原生微服务架构
我的运维人生
云原生架构腾讯云运维开发技术共享
腾讯云技术深度探索:构建高效云原生微服务架构在当今快速发展的技术环境中,云原生技术已成为企业数字化转型的关键驱动力。腾讯云作为行业领先的云服务提供商,不断推出创新的产品和技术,助力企业构建高效、可扩展的云原生微服务架构。本文将深入探讨腾讯云在微服务领域的最新进展,并通过一个实际案例展示如何在腾讯云平台上构建云原生应用。腾讯云微服务架构概览腾讯云微服务架构基于云原生理念,旨在帮助企业快速实现应用的容
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 使用 FinalShell 进行远程连接(ssh 远程连接 Linux 服务器)
编程经验分享
开发工具服务器sshlinux
目录前言基本使用教程新建远程连接连接主机自定义命令路由追踪前言后端开发,必然需要和服务器打交道,部署应用,排查问题,查看运行日志等等。一般服务器都是集中部署在机房中,也有一些直接是云服务器,总而言之,程序员不可能直接和服务器直接操作,一般都是通过ssh连接来登录服务器。刚接触远程连接时,使用的是XSHELL来远程连接服务器,连接上就能够操作远程服务器了,但是仅用XSHELL并没有上传下载文件的功能
- 2020-04-12每天三百字之连接与替代
冷眼看潮
不知道是不是好为人师,有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程,就是不断连接与替代的过程。人类发现了火并应用火以后,告别了茹毛饮血的野兽般的原始生活(火烧、烹饪替代了生食)人类用石器代替了完全手工,工具的使用使人类进步一大步。类似这样的替代还有很多,随着科技的发展,有更多的原始的事物被替代,代之以更高效、更先进的技术。在近现代,汽车替代了马车,高速公路和铁路
- 【加密社】Solidity 中的事件机制及其应用
加密社
闲侃区块链智能合约区块链
加密社引言在Solidity合约开发过程中,事件(Events)是一种非常重要的机制。它们不仅能够让开发者记录智能合约的重要状态变更,还能够让外部系统(如前端应用)监听这些状态的变化。本文将详细介绍Solidity中的事件机制以及如何利用不同的手段来触发、监听和获取这些事件。事件存储的地方当我们在Solidity合约中使用emit关键字触发事件时,该事件会被记录在区块链的交易收据中。具体而言,事件
- 使用Faiss进行高效相似度搜索
llzwxh888
faisspython
在现代AI应用中,快速和高效的相似度搜索是至关重要的。Faiss(FacebookAISimilaritySearch)是一个专门用于快速相似度搜索和聚类的库,特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索,并结合Python代码演示其基本用法。什么是Faiss?Faiss是一个由FacebookAIResearch团队开发的开源库,主要用于高维向量的相似性搜索和聚类。Faiss
- 使用Apify加载Twitter消息以进行微调的完整指南
nseejrukjhad
twittereasyui前端python
#使用Apify加载Twitter消息以进行微调的完整指南##引言在自然语言处理领域,微调模型以适应特定任务是提升模型性能的常见方法。本文将介绍如何使用Apify从Twitter导出聊天信息,以便进一步进行微调。##主要内容###使用Apify导出推文首先,我们需要从Twitter导出推文。Apify可以帮助我们做到这一点。通过Apify的强大功能,我们可以批量抓取和导出数据,适用于各类应用场景。
- 深入理解 MultiQueryRetriever:提升向量数据库检索效果的强大工具
nseejrukjhad
数据库python
深入理解MultiQueryRetriever:提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域,高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用,但仍存在一些局限性。本文将介绍一种创新的解决方案:MultiQueryRetriever,它通过自动生成多个查询视角来增强检索效果,提高结果的相关性和多样性。MultiQueryRetriever的工
- 利用LangChain的StackExchange组件实现智能问答系统
nseejrukjhad
langchainmicrosoft数据库python
利用LangChain的StackExchange组件实现智能问答系统引言在当今的软件开发世界中,StackOverflow已经成为程序员解决问题的首选平台之一。而LangChain作为一个强大的AI应用开发框架,提供了StackExchange组件,使我们能够轻松地将StackOverflow的海量知识库集成到我们的应用中。本文将详细介绍如何使用LangChain的StackExchange组件
- 在一台Ubuntu计算机上构建Hyperledger Fabric网络
落叶无声9
区块链超级账本Hyperledgerfabric区块链ubuntu构建hyperledgerfabric
在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台,为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时,我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件,部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
- MongoDB Oplog 窗口
喝醉酒的小白
MongoDB运维
在MongoDB中,oplog(操作日志)是一个特殊的日志系统,用于记录对数据库的所有写操作。oplog允许副本集成员(通常是从节点)应用主节点上已经执行的操作,从而保持数据的一致性。它是MongoDB副本集实现数据复制的基础。MongoDBOplog窗口oplog窗口是指在MongoDB副本集中,从节点可以用来同步数据的时间范围。这个窗口通常由以下因素决定:Oplog大小:oplog的大小是有限
- pyecharts——绘制柱形图折线图
2224070247
信息可视化pythonjava数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd)数据可视化团队研发的ECharts1.0发布到GitHub网站以来,ECharts一直备受业界权威的关注并获得广泛好评,成为目前成熟且流行的数据可视化图表工具,被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言,也加入ECharts的使用行列,并研发出方便Python开发者使用的数据
- CX8836:小体积大功率升降压方案推荐(附Demo设计指南)
诚芯微科技
社交电子
CX8836是一颗同步四开关单向升降压控制器,在4.5V-40V宽输入电压范围内稳定工作,持续负载电流10A,能够在输入高于或低于输出电压时稳定调节输出电压,可适用于USBPD快充、车载充电器、HUB、汽车启停系统、工业PC电源等多种升降压应用场合,为大功率TYPE-CPD车载充电器提供最优解决方案。提供CX8836Demo测试、CX8836样品申请及CX8836方案开发技术支持。CX8836同升
- 穷人做什么生意最赚钱?10个适合穷人赚钱的路子?
氧惠爱高省
不管在什么地方,一般都是穷人占大量数,而富人只有少数,但是它们却掌握着大量的财富。对于穷人来说,想要买车、买房等奢侈品就难如登天,因为他们只能通过打工来赚取几千元的月薪。➤推荐网购返利app“氧惠”,一个领隐藏优惠券+现金返利的平台。氧惠只提供领券返利链接,下单全程都在淘宝、京东、拼多多等原平台,更支持抖音、快手电商、外卖红包返利等。(应用市场搜“氧惠”下载,邀请码:521521,全网优惠上氧惠!
- 01-Git初识
Meereen
Gitgit
01-Git初识概念:一个免费开源,分布式的代码版本控制系统,帮助开发团队维护代码作用:记录代码内容。切换代码版本,多人开发时高效合并代码内容如何学:个人本机使用:Git基础命令和概念多人共享使用:团队开发同一个项目的代码版本管理Git配置用户信息配置:用户名和邮箱,应用在每次提交代码版本时表明自己的身份命令:查看git版本号git-v配置用户名gitconfig--globaluser.name
- 2019-05-13
王健_100a
【撒下18:2】大卫打发军兵出战,分为三队:一队在约押手下,一队在洗鲁雅的儿子约押兄弟亚比筛手下,一队在迦特人以太手下。大卫对军兵说:“我必与你们一同出战。”解释:大卫检阅部队,将它分成三队,每队由一位元帅统领;约押与兄弟亚比筛,并迦特人以太共同指挥。大卫想与他们一同出战!应用:作为领袖与军兵一起出战是很重要。领袖在事奉中与信徒一起,领袖在任何的环境里与信徒一起走过。我们要同心协力为主而战。祷告:
- 摩托车加装车载手机充电usb方案/雅马哈USB充电方案开发
诚芯微科技
社交电子
长途骑行需要给手机与行车记录仪等设备供电,那么,加装USB充电器就相继在两轮电动车上应用起来了。摩托车加装usb充电方案主要应用于汽车、电动自行车、摩托车、房车、渡轮、游艇等交通工具。提供电动车USB充电器方案/摩托车加装usb充电方案/渡轮加装usb充电方案/游艇加装usb充电方案开发。摩托车加装车载手机充电usb方案、汽车游艇改装四孔面板装双USB车充点烟器5V/4A电动车USB充电器输入4.
- 数字里的世界17期:2021年全球10大顶级数据中心,中国移动榜首
张三叨
你知道吗?2016年,全球的数据中心共计用电4160亿千瓦时,比整个英国的发电量还多40%!前言每天,我们都会创造超过250万TB的数据。并且随着物联网(IOT)的不断普及,这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代,但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术,比如人工智能和机器学习,已经将我们推向
- nosql数据库技术与应用知识点
皆过客,揽星河
NoSQLnosql数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
- 广州会刊小程序开发公司哪家好|开发多少钱费用|专业外包服务
红匣子实力推荐
在选择广州会刊小程序开发公司时,有几个关键因素需要考虑。首先,您应该确定自己的需求和目标,以便找到最合适的开发公司。其次,您需要考虑公司的经验和专业知识。最后,您还应该考虑公司的信誉和口碑。开发-联系电话:13642679953(微信同号)首先,您应该明确自己的需求和目标。会刊小程序是一种用于展示会议信息和日程安排的应用程序。在选择开发公司之前,您应该明确自己的需求,包括功能要求、设计风格和用户体
- 简介Shell、zsh、bash
zhaosuningsn
Shellzshbashshelllinuxbash
Shell是Linux和Unix的外壳,类似衣服,负责外界与Linux和Unix内核的交互联系。例如接收终端用户及各种应用程序的命令,把接收的命令翻译成内核能理解的语言,传递给内核,并把内核处理接收的命令的结果返回给外界,即Shell是外界和内核沟通的桥梁或大门。Linux和Unix提供了多种Shell,其中有种bash,当然还有其他好多种。Mac电脑中不但有bash,还有一个zsh,预装的,据说
- OPENAIGC开发者大赛企业组AI黑马奖 | AIGC数智传媒解决方案
RPA中国
人工智能AIGC传媒
在第二届拯救者杯OPENAIGC开发者大赛中,涌现出一批技术突出、创意卓越的作品。为了让这些优秀项目被更多人看到,我们特意开设了优秀作品报道专栏,旨在展示其独特之处和开发者的精彩故事。无论您是技术专家还是爱好者,希望能带给您不一样的知识和启发。让我们一起探索AIGC的无限可能,见证科技与创意的完美融合!创未来AI应用赛-企业组AI黑马奖作品名称:AIGC数智传媒解决方案参赛团队:深圳市三象智能技术
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- ES聚合分析原理与代码实例讲解
光剑书架上的书
大厂Offer收割机面试题简历程序员读书硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
ES聚合分析原理与代码实例讲解1.背景介绍1.1问题的由来在大规模数据分析场景中,特别是在使用Elasticsearch(ES)进行数据存储和检索时,聚合分析成为了一个至关重要的功能。聚合分析允许用户对数据集进行细分和分组,以便深入探索数据的结构和模式。这在诸如实时监控、日志分析、业务洞察等领域具有广泛的应用。1.2研究现状目前,ES聚合分析已经成为现代大数据平台的核心组件之一。它支持多种类型的聚
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- jsonp 常用util方法
hw1287789687
jsonpjsonp常用方法jsonp callback
jsonp 常用java方法
(1)以jsonp的形式返回:函数名(json字符串)
/***
* 用于jsonp调用
* @param map : 用于构造json数据
* @param callback : 回调的javascript方法名
* @param filters : <code>SimpleBeanPropertyFilter theFilt
- 多线程场景
alafqq
多线程
0
能不能简单描述一下你在java web开发中需要用到多线程编程的场景?0
对多线程有些了解,但是不太清楚具体的应用场景,能简单说一下你遇到的多线程编程的场景吗?
Java多线程
2012年11月23日 15:41 Young9007 Young9007
4
0 0 4
Comment添加评论关注(2)
3个答案 按时间排序 按投票排序
0
0
最典型的如:
1、
- Maven学习——修改Maven的本地仓库路径
Kai_Ge
maven
安装Maven后我们会在用户目录下发现.m2 文件夹。默认情况下,该文件夹下放置了Maven本地仓库.m2/repository。所有的Maven构件(artifact)都被存储到该仓库中,以方便重用。但是windows用户的操作系统都安装在C盘,把Maven仓库放到C盘是很危险的,为此我们需要修改Maven的本地仓库路径。
- placeholder的浏览器兼容
120153216
placeholder
【前言】
自从html5引入placeholder后,问题就来了,
不支持html5的浏览器也先有这样的效果,
各种兼容,之前考虑,今天测试人员逮住不放,
想了个解决办法,看样子还行,记录一下。
【原理】
不使用placeholder,而是模拟placeholder的效果,
大概就是用focus和focusout效果。
【代码】
<scrip
- debian_用iso文件创建本地apt源
2002wmj
Debian
1.将N个debian-506-amd64-DVD-N.iso存放于本地或其他媒介内,本例是放在本机/iso/目录下
2.创建N个挂载点目录
如下:
debian:~#mkdir –r /media/dvd1
debian:~#mkdir –r /media/dvd2
debian:~#mkdir –r /media/dvd3
….
debian:~#mkdir –r /media
- SQLSERVER耗时最长的SQL
357029540
SQL Server
对于DBA来说,经常要知道存储过程的某些信息:
1. 执行了多少次
2. 执行的执行计划如何
3. 执行的平均读写如何
4. 执行平均需要多少时间
列名 &
- com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil
7454103
eclipse
今天eclipse突然报了com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 错误,并且工程文件打不开了,在网上找了一下资料,然后按照方法操作了一遍,好了,解决方法如下:
错误提示信息:
An error has occurred.See error log for more details.
Reason:
com/genuitec/
- 用正则删除文本中的html标签
adminjun
javahtml正则表达式去掉html标签
使用文本编辑器录入文章存入数据中的文本是HTML标签格式,由于业务需要对HTML标签进行去除只保留纯净的文本内容,于是乎Java实现自动过滤。
如下:
public static String Html2Text(String inputString) {
String htmlStr = inputString; // 含html标签的字符串
String textSt
- 嵌入式系统设计中常用总线和接口
aijuans
linux 基础
嵌入式系统设计中常用总线和接口
任何一个微处理器都要与一定数量的部件和外围设备连接,但如果将各部件和每一种外围设备都分别用一组线路与CPU直接连接,那么连线
- Java函数调用方式——按值传递
ayaoxinchao
java按值传递对象基础数据类型
Java使用按值传递的函数调用方式,这往往使我感到迷惑。因为在基础数据类型和对象的传递上,我就会纠结于到底是按值传递,还是按引用传递。其实经过学习,Java在任何地方,都一直发挥着按值传递的本色。
首先,让我们看一看基础数据类型是如何按值传递的。
public static void main(String[] args) {
int a = 2;
- ios音量线性下降
bewithme
ios音量
直接上代码吧
//second 几秒内下降为0
- (void)reduceVolume:(int)second {
KGVoicePlayer *player = [KGVoicePlayer defaultPlayer];
if (!_flag) {
_tempVolume = player.volume;
- 与其怨它不如爱它
bijian1013
选择理想职业规划
抱怨工作是年轻人的常态,但爱工作才是积极的心态,与其怨它不如爱它。
一般来说,在公司干了一两年后,不少年轻人容易产生怨言,除了具体的埋怨公司“扭门”,埋怨上司无能以外,也有许多人是因为根本不爱自已的那份工作,工作完全成了谋生的手段,跟自已的性格、专业、爱好都相差甚远。
- 一边时间不够用一边浪费时间
bingyingao
工作时间浪费
一方面感觉时间严重不够用,另一方面又在不停的浪费时间。
每一个周末,晚上熬夜看电影到凌晨一点,早上起不来一直睡到10点钟,10点钟起床,吃饭后玩手机到下午一点。
精神还是很差,下午像一直野鬼在城市里晃荡。
为何不尝试晚上10点钟就睡,早上7点就起,时间完全是一样的,把看电影的时间换到早上,精神好,气色好,一天好状态。
控制让自己周末早睡早起,你就成功了一半。
有多少个工作
- 【Scala八】Scala核心二:隐式转换
bit1129
scala
Implicits work like this: if you call a method on a Scala object, and the Scala compiler does not see a definition for that method in the class definition for that object, the compiler will try to con
- sudoku slover in Haskell (2)
bookjovi
haskellsudoku
继续精简haskell版的sudoku程序,稍微改了一下,这次用了8行,同时性能也提高了很多,对每个空格的所有解不是通过尝试算出来的,而是直接得出。
board = [0,3,4,1,7,0,5,0,0,
0,6,0,0,0,8,3,0,1,
7,0,0,3,0,0,0,0,6,
5,0,0,6,4,0,8,0,7,
- Java-Collections Framework学习与总结-HashSet和LinkedHashSet
BrokenDreams
linkedhashset
本篇总结一下两个常用的集合类HashSet和LinkedHashSet。
它们都实现了相同接口java.util.Set。Set表示一种元素无序且不可重复的集合;之前总结过的java.util.List表示一种元素可重复且有序
- 读《研磨设计模式》-代码笔记-备忘录模式-Memento
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
/*
* 备忘录模式的功能是,在不破坏封装性的前提下,捕获一个对象的内部状态,并在对象之外保存这个状态,为以后的状态恢复作“备忘”
- 《RAW格式照片处理专业技法》笔记
cherishLC
PS
注意,这不是教程!仅记录楼主之前不太了解的
一、色彩(空间)管理
作者建议采用ProRGB(色域最广),但camera raw中设为ProRGB,而PS中则在ProRGB的基础上,将gamma值设为了1.8(更符合人眼)
注意:bridge、camera raw怎么设置显示、输出的颜色都是正确的(会读取文件内的颜色配置文件),但用PS输出jpg文件时,必须先用Edit->conv
- 使用 Git 下载 Spring 源码 编译 for Eclipse
crabdave
eclipse
使用 Git 下载 Spring 源码 编译 for Eclipse
1、安装gradle,下载 http://www.gradle.org/downloads
配置环境变量GRADLE_HOME,配置PATH %GRADLE_HOME%/bin,cmd,gradle -v
2、spring4 用jdk8 下载 https://jdk8.java.
- mysql连接拒绝问题
daizj
mysql登录权限
mysql中在其它机器连接mysql服务器时报错问题汇总
一、[running]
[email protected]:~$mysql -uroot -h 192.168.9.108 -p //带-p参数,在下一步进行密码输入
Enter password: //无字符串输入
ERROR 1045 (28000): Access
- Google Chrome 为何打压 H.264
dsjt
applehtml5chromeGoogle
Google 今天在 Chromium 官方博客宣布由于 H.264 编解码器并非开放标准,Chrome 将在几个月后正式停止对 H.264 视频解码的支持,全面采用开放的 WebM 和 Theora 格式。
Google 在博客上表示,自从 WebM 视频编解码器推出以后,在性能、厂商支持以及独立性方面已经取得了很大的进步,为了与 Chromium 现有支持的編解码器保持一致,Chrome
- yii 获取控制器名 和方法名
dcj3sjt126com
yiiframework
1. 获取控制器名
在控制器中获取控制器名: $name = $this->getId();
在视图中获取控制器名: $name = Yii::app()->controller->id;
2. 获取动作名
在控制器beforeAction()回调函数中获取动作名: $name =
- Android知识总结(二)
come_for_dream
android
明天要考试了,速速总结如下
1、Activity的启动模式
standard:每次调用Activity的时候都创建一个(可以有多个相同的实例,也允许多个相同Activity叠加。)
singleTop:可以有多个实例,但是不允许多个相同Activity叠加。即,如果Ac
- 高洛峰收徒第二期:寻找未来的“技术大牛” ——折腾一年,奖励20万元
gcq511120594
工作项目管理
高洛峰,兄弟连IT教育合伙人、猿代码创始人、PHP培训第一人、《细说PHP》作者、软件开发工程师、《IT峰播》主创人、PHP讲师的鼻祖!
首期现在的进程刚刚过半,徒弟们真的很棒,人品都没的说,团结互助,学习刻苦,工作认真积极,灵活上进。我几乎会把他们全部留下来,现在已有一多半安排了实际的工作,并取得了很好的成绩。等他们出徒之日,凭他们的能力一定能够拿到高薪,而且我还承诺过一个徒弟,当他拿到大学毕
- linux expect
heipark
expect
1. 创建、编辑文件go.sh
#!/usr/bin/expect
spawn sudo su admin
expect "*password*" { send "13456\r\n" }
interact
2. 设置权限
chmod u+x go.sh 3.
- Spring4.1新特性——静态资源处理增强
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- idea ubuntuxia 乱码
liyonghui160com
1.首先需要在windows字体目录下或者其它地方找到simsun.ttf 这个 字体文件。
2.在ubuntu 下可以执行下面操作安装该字体:
sudo mkdir /usr/share/fonts/truetype/simsun
sudo cp simsun.ttf /usr/share/fonts/truetype/simsun
fc-cache -f -v
- 改良程序的11技巧
pda158
技巧
有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点,程序你只写一次,但以后会无数次的阅读。当你第二天回头来看你的代码 时,你就要开始阅读它了。当你把代码拿给其他人看时,他必须阅读你的代码。因此,在编写时多花一点时间,你会在阅读它时节省大量的时间。
让我们看一些基本的编程技巧:
尽量保持方法简短
永远永远不要把同一个变量用于多个不同的
- 300个涵盖IT各方面的免费资源(下)——工作与学习篇
shoothao
创业免费资源学习课程远程工作
工作与生产效率:
A. 背景声音
Noisli:背景噪音与颜色生成器。
Noizio:环境声均衡器。
Defonic:世界上任何的声响都可混合成美丽的旋律。
Designers.mx:设计者为设计者所准备的播放列表。
Coffitivity:这里的声音就像咖啡馆里放的一样。
B. 避免注意力分散
Self Co
- 深入浅出RPC
uule
rpc
深入浅出RPC-浅出篇
深入浅出RPC-深入篇
RPC
Remote Procedure Call Protocol
远程过程调用协议
它是一种通过网络从远程计算机程序上请求服务,而不需要了解底层网络技术的协议。RPC协议假定某些传输协议的存在,如TCP或UDP,为通信程序之间携带信息数据。在OSI网络通信模型中,RPC跨越了传输层和应用层。RPC使得开发
![]()
![]()