吴恩达机器学习 线性回归 作业(房价预测) Python实现 代码详细解释

 

整个项目的github:https://github.com/RobinLuoNanjing/MachineLearning_Ng_Python

里面可以下载进行代码实现的数据集data.txt或data.csv

 

介绍：

最近在看吴恩达机器学习视频的时候，为了巩固自己的基础，想亲自实现一下课程里面的每个算法。在实现之前，我先看了一下别人实现的相关代码，看完就特别沮丧，很多人的代码，要么就是完全没注释，要么就是注释了关键点，有些细节甚至技巧简直深藏不露，对我这样的渣渣实在是不太友好。

俗话说万事开头难，实现线性回归确实花了我很多时间，不过实现完了就贼开心了，不仅熟悉了python,numpy,pandas等各种操作，还让自己对枯燥的数学公式有了质的理解。好在我这次实现的过程中，对很多细节都留了注释，虽然冗长，但是很适合新手去慢慢推敲。

当然，代码中也有很多问题，或者说不够优化的地方，希望能在讨论中不断改进。当然，改进算法不是最重要的，这些机器学习算法早被封装好了，其实讨论学习才是我的目的所在。

 

题目：

In this part, you will implement linear regression with multiple variables to predict the prices of houses. Suppose you are selling your house and you want to know what a good market price would be. One way to do this is to first collect information on recent houses sold and make a model of housing prices.

 

翻译：

在这里，您将使用多个变量用来实现线性回归来预测房屋的价格。假设你在卖房子，你想知道一个好的市场价格是多少。这样做的一个方法是首先收集最近售出的房屋的信息，并制作一个房价模型。

 

 

 

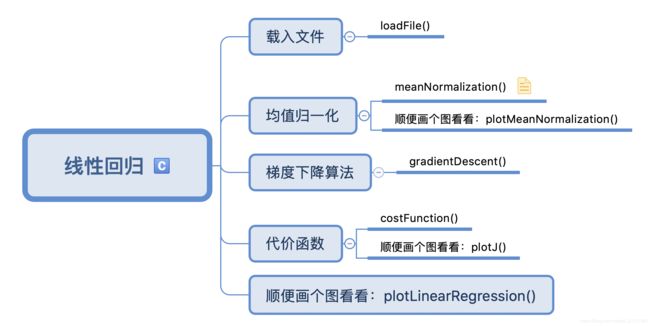
代码结构图：

 

思考步骤：

首先设置一个线性回归函数：linearRegression()，我们在后来将在这个函数里调用很多其他函数。下面的linearRegression函数一定会让初学者看着就崩溃。稍安勿躁，一步一步分解，就能理解很多只看书学不到的细节。

def linearRegression(alpha=0.01, num_iters=400):    #学习速率为0.01，迭代次数为400
    data=loadFile('data.csv')   #步骤1 先载入文件

    X=np.array(data[:,0:-1])   #步骤2 对载入的数据进行提取。具体看思考
    y=np.array(data[:,-1]).reshape(-1,1) #这里一定要将y数组转换为47行1列的二维数组，不然后面计算肯定全部报错

    X=meanNormalization(X)     #步骤3 进行均值归一化操作 。这里需不需要对y进行均值归一化？？？其实我也很疑问，因为我尝试过归一化，发现结果与没归一化一样。算是给我留个问题，等我后来解决

    plotMeanNormalization(X)   #步骤4 画图
    X=np.hstack((np.ones((len(y),1)),X))   #步骤5 插入一列全为1的数组。   这里利用np.hstack()函数进行插入，前一个参数是插入的矩阵的形状，后一个参数是插入到哪个矩阵中

    num_theta=X.shape[1]
    theta=np.zeros((num_theta,1))    #步骤6 theta是我们想要求出的参数，我们构建一个3行1列的零矩阵用来存放theta。
    y=y.reshape(-1,1)      #将y转置，变为一个向量。超级注意！这里不能用y.T。因为y原来是个一维数组，写y.T依旧是个一维数组，不是向量

    thetaValue,J_all=gradientDescent(X,y,theta,alpha,num_iters)   #步骤7 调用梯度下降算法  返回的thetaValue,就是让函数收敛的theta值

    plotJ(J_all,num_iters)  #步骤9 画J曲线
    plotLinearRegression(X, thetaValue,y)
    return thetaValue

1. 创建一个loadFile()函数负责导入文件,并且返回一个np数组。

   #载入文件函数
   def loadFile(path):
       return np.loadtxt(path,delimiter=',',dtype=np.float64)    #此处调用的是np.loadtxt()方法加载csv文件，分隔符采用','，数据类型为np.float64

2. 这个时候，因为我们已经获得了导入文件的数据，需要对导入文件数据进行处理：X作为一个两列的矩阵，存放第一列(square)和第二列(room)，y作为一个向量，存放的是最后一列，房价的实际价格(price)。

   data=loadFile('data.csv')   #步骤1 先载入文件
   
   X=np.array(data[:,0:-1])   #步骤2 对载入的数据进行提取。具体看思考
   y=np.array(data[:,-1]).reshape(-1,1) #这里一定要将y数组转换为47行1列的二维数组，不然后面计算肯定全部报错

3. 紧接着，我们需要创建一个meanNormalization(X)函数，进行均值归一化操作。

   def meanNormalization(X):
       columnsMean=np.mean(X,0)    #求出了每一列的平均值，注：0表示求列的均值，1表示求行的均值
       columnsStd=np.std(X,0)      #求出了每一列的标准差，注：0表示求列的标准差值，1表示求行的标准差
   
       #接下来我们需要对每一列的值都进行归一化操作，所以我们要枚举每一列
       for i in range(X.shape[1]):
           X[:,i]=(X[:,i]-columnsMean[i])/columnsStd[i]       #归一化操作，X的每一列中的每一行值都会减去当前列的均值，然后除去方差。
       return X                                             #值得注意的是，只有numpy.array类型才能做这样的矩阵操作。不然的话，你选取了n行1列的数组，减去一个均值，会报错。
   

    我写了两个均值归一化函数，下面这个整个流程看起来比较清爽

   def meanNormalization(X):
       return np.apply_along_axis((lambda column: (column - column.mean()) / column.std()), 0, X)

4. 当我们完成均值归一化操作之后，我们可以用plotMeanNormalization()函数查看一下均值归一化的效果。

   #画图均值归一化函数
   def plotMeanNormalization(X):
       plt.scatter(X[:,0],X[:,1])     #将第一列数据转化为x轴数据，将第二列数据转化为y轴数据
       plt.show()

5. 根据吴恩达视频中的说明，我们需要对均值归一化过的矩阵插入新的一列，这一列全为1，并且放在第0列。

   X=np.hstack((np.ones((len(y),1)),X))   #步骤5 插入一列全为1的数组。   这里利用np.hstack()函数进行插入，前一个参数是插入的矩阵的形状，后一个参数是插入到哪个矩阵中

6. 紧接着我们要着手考虑下theta，因为theta是我们想要求出的参数。这里theta的数量正好等于X矩阵的列数。所以我们构建一个3行1列的零矩阵，用来放theta，theta的初始值为0。

   theta=np.zeros((num_theta,1))    #步骤6 theta是我们想要求出的参数，我们构建一个3行1列的零矩阵用来存放theta。

7. 我们现在有了所有需要的数据，这个时候就要开始梯度下降算法了。这里应该是整个代码最难理解的地方。
   7.1 首先我们需要知道，代价函数J为了计算现实数据与假设函数h中的数据的误差。而梯度下降算法是不断的寻找一个theta集合，这个集合使代价函数的值最小。
   7.2 创建一个temp_theta的矩阵，用来存放每一次迭代的theta。
   7.3 创建一个J_all矩阵，用来存放用theta求出的代价函数的值。有多少组theta就有多少组代价函数值。
   7.4 利用for循环，每次循环就是一次迭代，因为刚开始我们设置的迭代次数 num_iters=400，所以就有400次迭代。
   7.5 接下来就是梯度下降算法的核心，比较难理解，我把细节解释写在了注释里。
   7.6 每次迭代，我们都要计算代价函数值，这样把400次迭代的代价函数值放在一起，我们只要观察到代价函数值在下降，说明这个算法有效果。代价函数怎么构造，请看步骤8。

   def gradientDescent(X,y,theta,alpha,num_iters):
       m=len(y)      #获得y矩阵的个数
       num_theta=len(theta)  #获取theta向量的个数
   
       temp_theta=np.matrix(np.zeros((num_theta,num_iters)))  #步骤7.2 ：这里的temp矩阵存放每一次迭代的theta情况。此条件下，该矩阵是3x400,每一列存放一次迭代的所有theta情况
                                                               #这里要加一个matrix，比较恶心的地方，原因往下看。
   
       J_all=np.zeros((num_iters,1))                                                #步骤7.3 ：这里存放的是每一次迭代情况下的代价函数的代价值。为什么要临时存放呢？当然是为了作图了
   
   
       #步骤7.4 ：准备开始迭代了
       for i in range(num_iters):              #迭代次数当然是num_iters
           hypothesis=np.dot(X,theta)         #X与theta内积：有点像假设函数的展开，自己手写一下X*theta,或许就会明白了。默认theta的初始值为0
           temp_theta[:,i]=theta-(alpha/m)*(np.dot(np.transpose(X),hypothesis-y))  #梯度下降的核心公式。  注意！！！为什么之前的temp_theta要加matrix?因为如果不加matrix,
                                                                                   #你对temp_theta进行切片操作，取出来的不是一个n行1列的数组，而是一个一维数组！！！如果不加matrix
                                                                                   #后面一定报错(3,1)的矩阵放不进一个(3,)的一维数组里
           theta=temp_theta[:,i]                                                   #这里需要从temp_theta里取出当前迭代的theta值。有什么用？我得用这个来算当前theta影响的J代价函数的值。
   
           J_all[i]=costFunction(X,theta,y)
       thetaValue=theta          #最后一个theta里存放的是最后一次迭代，趋于收敛的theta值，我们将这个结果返回
       return thetaValue,J_all                                                               #注意了，J_all原来只是局部变量，得把它返回，不然linearRegression函数使用不了这个数据
   

   这里我想详细解释下7.5步骤提到的会让你捉摸不透的那行代码：

   temp_theta[:,i]=theta-(alpha/m)*(np.dot(np.transpose(X),hypothesis-y))

   1.temp_theta[:,i]     ：实际上在每次迭代，我都把theta的新数据导入到这个矩阵里的一列
   2. (alpha/m) 其实不用多说，就是学习速率除去样本总数m
   3. (np.dot(np.transpose(X),hypothesis-y))    这个我们需要拆分着看。
       3.1 先看   hypothesis-y  :这个其实就是生成一个新的矩阵，在此数据下，是47x1的矩阵。矩阵存放着47个样本的 h(x)-y。
       3.2 再看 np.transpose(X)   :就是把X转置。
       3.3 最后看np.dot 也就是3.1和3.2的内积。是一个3x47的矩阵乘一个47x1的矩阵，生成一个3x1的矩阵。这里建议大家写一个草稿，去模拟这个内积的效果，比较容易弄明白。

8. 代价函数名就叫costFunction(),这个函数是不会在linearRegression函数中调用的，而是gradientDescent()函数调用的。
   8.1 costFunction(X,theta,y),第一个参数就是我们的数据X，第二个参数就是每次代入的theta值（注意！！！这里的theta都是由梯度下降算法求出来的一组theta，而非主函数里的theta）
   8.2 代入直接计算代价值。

   #代价函数
   def costFunction(X,theta,y):
       m=len(y)      #先算出有m条数据
       J=0           #初始化代价函数为0
   
       J=np.sum(np.power(np.dot(X,theta)-y,2))/(2*m)          #步骤8.2  ：这里用了np.power(arr,n) 进行二次方运算，注意，只是对每个元素进行二次方运算，返回的还是一个47x1的矩阵，所以要相加这47个值除去2m。
   
   
       # J=np.dot([(np.dot(X,theta)-y).T],np.dot(X,theta)-y)/(2*m)    #虽然这个J看起来复杂一点，但是它是(X*theta-y).T * (X*theta-y) ,可以直接返回一个值，而非一个列表
   
   
       return J

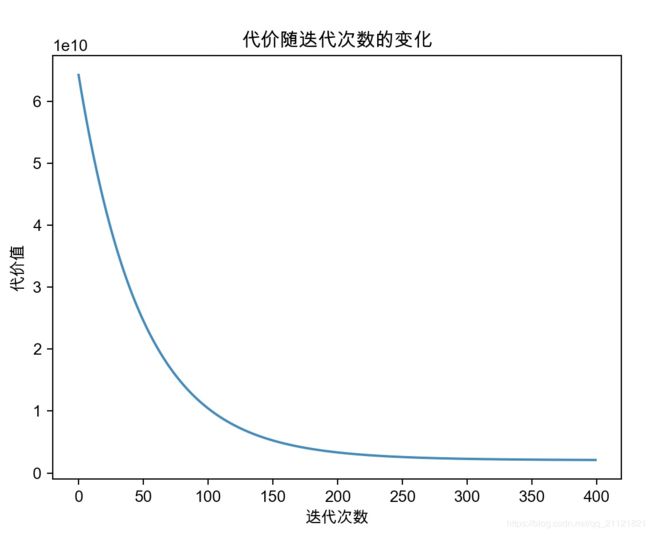
9. 梯度下降函数返回两个值，一个是让函数收敛的theta值。另外一个是每次迭代算出的代价函数值。现在我们要创建一个plotJ函数，用来代价值的变化。生成的图片表示，代价确实是不断减小的，说明函数收敛了。

   #画代价值的变化曲线
   def plotJ(J_all, num_iters):
       x = np.arange(0, num_iters)
       plt.plot(x, J_all)
       plt.xlabel("迭代次数")  # 如果出现乱码，需要修改代码第八行的相关参数
       plt.ylabel("代价值")
       plt.title("代价随迭代次数的变化")
       plt.show()

10. 最后，为了炫技，我们需要用plotLinearRegression(X,thetaValue,price)函数，以3D的形式表现其中迭代的过程。实际上，这个3D图像利用的是使函数拟合的theta值，展现的一次迭代的效果。

    #画3D过程图
    def plotLinearRegression(X,thetaValue,price):
        plt.figure(figsize=(8,10))
        x = X[:,1]
        y = X[:,2]
    
        thetaValue=thetaValue.flatten()     #将thetaValue转换为1维
    
    
        z = thetaValue[0, 0] + (thetaValue[0, 1] * x) + (thetaValue[0, 2] * y)
    
    
        ax=plt.subplot(211,projection='3d')
        ax.plot_trisurf(x,y,z)
        ax.scatter(X[:,1],X[:,2],price,label='实际数据')
    
    
        ax.set_xlabel('房屋大小')
        ax.set_ylabel('房间数')
        ax.set_zlabel('价格')
        plt.show()

     

 

图片效果：

1. 先看看plotMeanNormalization(X)函数画出来的图。显示的就是X矩阵归一化的效果。

   

2. 我们再看看plotJ()函数画出来的效果。显示的是400次迭代的代价值得变化。可以看出，代价一直在降低，说明这个算法起到了作用。

   

3. 最后我们看看plotLinearRegression()函数的效果图。这个图是根据我们将代价取得最小值时，使用的那一组theta的值。

   

完整代码：

import numpy as np
import matplotlib
from matplotlib import pyplot as plt
import mpl_toolkits.mplot3d.axes3d as Axes3D


np.set_printoptions(suppress=True, threshold=np.nan)    #去除科学计数法，不然看起来太难受了，都是e01啥的
matplotlib.rcParams['font.family']='Arial Unicode MS' #mac环境下防止中文乱码

'''
首先设置一个线性回归函数：linearRegression()，我们在后来将在这个函数里调用很多其他函数

思考步骤：
1.创建一个loadFile()函数负责导入文件,并且返回一个np数组
2.这个时候，因为我们已经获得了导入文件的数据，需要对导入文件数据进行处理：X作为一个两列的矩阵，存放第一列(square)和第二列(room)，
    y作为一个向量，存放的是最后一列，房价的实际价格(price)
3.紧接着，我们需要创建一个meanNormalization(X)函数，进行均值归一化操作.
4.当我们完成均值归一化操作之后，我们可以用plotMeanNormalization()函数查看一下均值归一化的效果
5.根据吴恩达视频中的说明，我们需要对均值归一化过的矩阵插入新的一列，这一列全为1，并且放在第0列
6.紧接着我们要着手考虑下theta，因为theta是我们想要求出的参数。这里theta的数量正好等于X矩阵的列数。所以我们构建一个3行1列的零矩阵，用来放theta，theta的初始值为0.
7.我们现在有了所有需要的数据，这个时候就要开始梯度下降算法了。这里应该是整个代码最难理解的地方。
    7.1 首先我们需要知道，代价函数J为了计算现实数据与假设函数h中的数据的误差。而梯度下降算法是不断的寻找一个theta集合，这个集合使代价函数的值最小。
    7.2 创建一个temp_theta的矩阵，用来存放每一次迭代的theta。
    7.3 创建一个J_all矩阵，用来存放用theta求出的代价函数的值。有多少组theta就有多少组代价函数值
    7.4 利用for循环，每次循环就是一次迭代，因为刚开始我们设置的迭代次数 num_iters=400，所以就有400次迭代。
    7.5 接下来就是梯度下降算法的核心，比较难理解，我把细节解释写在了注释里
    7.6 每次迭代，我们都要计算代价函数值，这样把400次迭代的代价函数值放在一起，我们只要观察到代价函数值在下降，说明这个算法有效果。代价函数怎么构造，请看步骤8
8.代价函数名就叫costFunction(),这个函数是不会在linearRegression函数中调用的，而是gradientDescent()函数调用的。
    8.1 costFunction(X,theta,y),第一个参数就是我们的数据X，第二个参数就是每次代入的theta值（注意！！！这里的theta都是由梯度下降算法求出来的一组theta，而非主函数里的theta）
    8.2 代入直接计算代价值
9.梯度下降函数返回两个值，一个是让函数收敛的theta值。另外一个是每次迭代算出的代价函数值。现在我们要创建一个plotJ函数，用来代价值的变化。生成的图片表示，代价确实是不断减小的，说明函数收敛了。
10.最后，为了炫技，我们需要用plotLinearRegression(X,thetaValue,price)函数，以3D的形式表现其中迭代的过程。
    实际上，这个3D图像利用的是使函数拟合的theta值，展现的一次迭代的效果。


'''

def linearRegression(alpha=0.01, num_iters=400):    #学习速率为0.01，迭代次数为400
    data=loadFile('data.csv')   #步骤1 先载入文件

    X=np.array(data[:,0:-1])   #步骤2 对载入的数据进行提取。具体看思考
    y=np.array(data[:,-1]).reshape(-1,1) #这里一定要将y数组转换为47行1列的二维数组，不然后面计算肯定全部报错

    X=meanNormalization(X)     #步骤3 进行均值归一化操作 。这里需不需要对y进行均值归一化？？？其实我也很疑问，因为我尝试过归一化，发现结果与没归一化一样。算是给我留个问题，等我后来解决

    plotMeanNormalization(X)   #步骤4 画图
    X=np.hstack((np.ones((len(y),1)),X))   #步骤5 插入一列全为1的数组。   这里利用np.hstack()函数进行插入，前一个参数是插入的矩阵的形状，后一个参数是插入到哪个矩阵中

    num_theta=X.shape[1]
    theta=np.zeros((num_theta,1))    #步骤6 theta是我们想要求出的参数，我们构建一个3行1列的零矩阵用来存放theta。
    y=y.reshape(-1,1)      #将y转置，变为一个向量。超级注意！这里不能用y.T。因为y原来是个一维数组，写y.T依旧是个一维数组，不是向量

    thetaValue,J_all=gradientDescent(X,y,theta,alpha,num_iters)   #步骤7 调用梯度下降算法  返回的thetaValue,就是让函数收敛的theta值

    plotJ(J_all,num_iters)  #步骤9 画J曲线
    plotLinearRegression(X, thetaValue,y)
    return thetaValue


#载入文件函数
def loadFile(path):
    return np.loadtxt(path,delimiter=',',dtype=np.float64)    #此处调用的是np.loadtxt()方法加载csv文件，分隔符采用','，数据类型为np.float64




# #均值归一化函数
def meanNormalization(X):
    columnsMean=np.mean(X,0)    #求出了每一列的平均值，注：0表示求列的均值，1表示求行的均值
    columnsStd=np.std(X,0)      #求出了每一列的标准差，注：0表示求列的标准差值，1表示求行的标准差

    #接下来我们需要对每一列的值都进行归一化操作，所以我们要枚举每一列
    for i in range(X.shape[1]):
        X[:,i]=(X[:,i]-columnsMean[i])/columnsStd[i]       #归一化操作，X的每一列中的每一行值都会减去当前列的均值，然后除去方差。
    return X                                             #值得注意的是，只有numpy.array类型才能做这样的矩阵操作。不然的话，你选取了n行1列的数组，减去一个均值，会报错。

'''
这是我写的第二个均值归一化的函数，其特点就是利用了numpy.apply_along_axis()函数实现的超简洁模式，
理解上可能有点困难，并且在小数据量的情况下，速度是不如上一个函数的，所以我暂时注释掉

def meanNormalization(X):
    return np.apply_along_axis((lambda column: (column - column.mean()) / column.std()), 0, X)
'''





#画图均值归一化函数
def plotMeanNormalization(X):
    plt.scatter(X[:,0],X[:,1])     #将第一列数据转化为x轴数据，将第二列数据转化为y轴数据
    plt.show()




#梯度下降算法
def gradientDescent(X,y,theta,alpha,num_iters):
    m=len(y)      #获得y矩阵的个数
    num_theta=len(theta)  #获取theta向量的个数

    temp_theta=np.matrix(np.zeros((num_theta,num_iters)))  #步骤7.2 ：这里的temp矩阵存放每一次迭代的theta情况。此条件下，该矩阵是3x400,每一列存放一次迭代的所有theta情况
                                                            #这里要加一个matrix，比较恶心的地方，原因往下看。

    J_all=np.zeros((num_iters,1))                                                #步骤7.3 ：这里存放的是每一次迭代情况下的代价函数的代价值。为什么要临时存放呢？当然是为了作图了


    #步骤7.4 ：准备开始迭代了
    for i in range(num_iters):              #迭代次数当然是num_iters
        hypothesis=np.dot(X,theta)         #X与theta内积：有点像假设函数的展开，自己手写一下X*theta,或许就会明白了。默认theta的初始值为0
        temp_theta[:,i]=theta-(alpha/m)*(np.dot(np.transpose(X),hypothesis-y))  #梯度下降的核心公式。  注意！！！为什么之前的temp_theta要加matrix?因为如果不加matrix,
                                                                                #你对temp_theta进行切片操作，取出来的不是一个n行1列的数组，而是一个一维数组！！！如果不加matrix
                                                                                #后面一定报错(3,1)的矩阵放不进一个(3,)的一维数组里
        theta=temp_theta[:,i]                                                   #这里需要从temp_theta里取出当前迭代的theta值。有什么用？我得用这个来算当前theta影响的J代价函数的值。

        J_all[i]=costFunction(X,theta,y)
    thetaValue=theta          #最后一个theta里存放的是最后一次迭代，趋于收敛的theta值，我们将这个结果返回
    return thetaValue,J_all                                                               #注意了，J_all原来只是局部变量，得把它返回，不然linearRegression函数使用不了这个数据

'''步骤7.5 ：讲解 梯度下降公式的细节
    1.temp_theta[:,i]     ：实际上在每次迭代，我都把theta的新数据导入到这个矩阵里的一列
    2. (alpha/m) 其实不用多说，就是学习速率除去样本总数m
    3. (np.dot(np.transpose(X),hypothesis-y))    这个我们需要拆分着看。
        3.1 先看   hypothesis-y  :这个其实就是生成一个新的矩阵，在此数据下，是47x1的矩阵。矩阵存放着47个样本的 h(x)-y。
        3.2 再看 np.transpose(X)   :就是把X转置。
        3.3 最后看np.dot 也就是3.1和3.2的内积。是一个3x47的矩阵乘一个47x1的矩阵，生成一个3x1的矩阵。这里建议大家写一个草稿，去模拟这个内积的效果，比较容易弄明白。
'''



#代价函数
def costFunction(X,theta,y):
    m=len(y)      #先算出有m条数据
    J=0           #初始化代价函数为0

    J=np.sum(np.power(np.dot(X,theta)-y,2))/(2*m)          #步骤8.2  ：这里用了np.power(arr,n) 进行二次方运算，注意，只是对每个元素进行二次方运算，返回的还是一个47x1的矩阵，所以要相加这47个值除去2m。


    # J=np.dot([(np.dot(X,theta)-y).T],np.dot(X,theta)-y)/(2*m)    #虽然这个J看起来复杂一点，但是它是(X*theta-y).T * (X*theta-y) ,可以直接返回一个值，而非一个列表


    return J

#画代价值的变化曲线
def plotJ(J_all, num_iters):
    x = np.arange(0, num_iters)
    plt.plot(x, J_all)
    plt.xlabel("迭代次数")  # 如果出现乱码，需要修改代码第八行的相关参数
    plt.ylabel("代价值")
    plt.title("代价随迭代次数的变化")
    plt.show()


#画3D过程图
def plotLinearRegression(X,thetaValue,price):
    plt.figure(figsize=(8,10))
    x = X[:,1]
    y = X[:,2]

    thetaValue=thetaValue.flatten()     #将thetaValue转换为1维


    z = thetaValue[0, 0] + (thetaValue[0, 1] * x) + (thetaValue[0, 2] * y)


    ax=plt.subplot(211,projection='3d')
    ax.plot_trisurf(x,y,z)
    ax.scatter(X[:,1],X[:,2],price,label='实际数据')


    ax.set_xlabel('房屋大小')
    ax.set_ylabel('房间数')
    ax.set_zlabel('价格')
    plt.show()


print('使函数收敛的theta值为：\n',linearRegression())