MATLAB最优化工具箱
参考网站:http://ww2.mathworks.cn/help/matlab/ref/fminbnd.html
1.一元函数极小值 x=fmindbnd('F(x)', a, b) ,a、b为所给小区间,在所给区间中求最小值。
%1
minx = fminbnd('x^2',-10,10);
%2
y = 'x^2';
minx = fminbnd(y,-10,10);
%3
y = @(x)x^2;
[minx,miny] = fminbnd(y,-10,10);
%4
y = @(x)x^2;
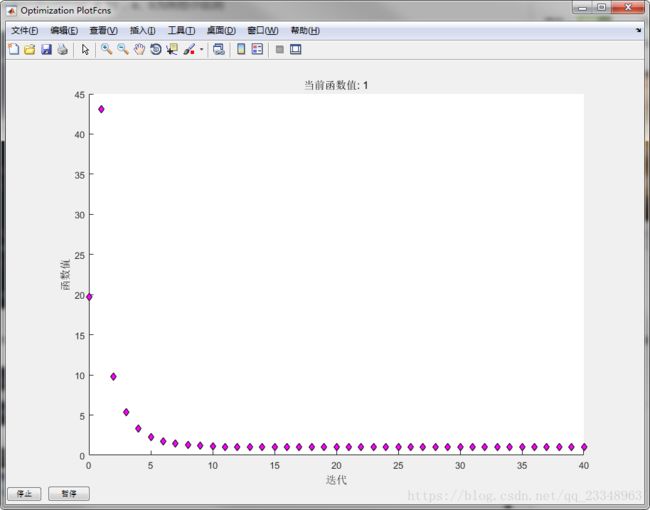
option = optimset('Display','iter','TolX',1e-10,'PlotFcns',@optimplotfval);
[minx,miny] = fminbnd(y,1,10,option);2.无约束极小值 X=fminsearch('F(x)', a)或者 X=fminunc('F(x)', a) ,在点 a处开始并尝试求F(x)中描述的函数的局部最小值 minx。
%1
y = @(x)x^2;
option = optimset('Display','iter','TolX',1e-10,'PlotFcns',@optimplotfval);
minx= fminsearch(y,10,option);
%2
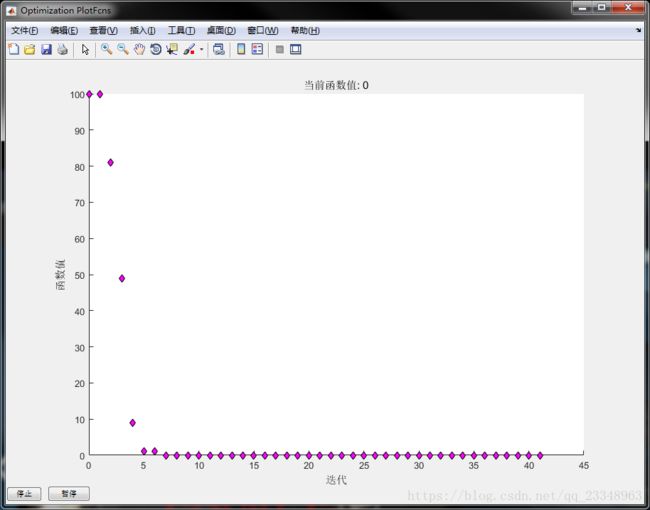
fun = @(x)100*(x(2) - 1)^2 + (x(1) - 1)^2 + (x(3) - 100)^2;
option = optimset('Display','iter','TolX',1e-10,'PlotFcns',@optimplotfval);
xstart = [-55,1,1];
[minx,miny,exitflag,output] = fminsearch(fun,xstart,option);
%3
fun = @(x)100*(x(2) - 1)^2 + (x(1) - 1)^2 + (x(3) - 100)^2;
option = optimset('Display','iter','TolX',1e-10,'PlotFcns',@optimplotfval);
xstart = [-55,1,1];
[minx,miny,exitflag,output] = fminunc(fun,xstart,option);可求多元方程的最小是问题,另外fminsearch用的是Nelder-Mead simplex direct search算法,fminunc用的是quasi-newton(拟牛顿法),代码二迭代209次,代码三只迭代2次,用时大大缩小。
3.线性规划 X=linprog(c,A,b),A矩阵和b向量为线性不等式约束:Ax≤b的系数矩阵和右端向量。
%1
A = [1 1;
1 1/4
1 -1
-1/4 -1
-1 -1
-1 1];
b = [2 1 2 1 -1 2];
f = [-1 -1/3];
Aeq = [1 1/4];
beq = 1/2;
lb = [-1,-0.5];
ub = [1.5,1.25];
option = optimset('Display','iter','TolX',1e-10,'PlotFcns',@optimplotfval);
[x,fval,exitflag,output] = linprog(f,A,b,Aeq,beq,lb,ub,option)
%2
f = [-5 -4 -6];
A = [1 -1 1
3 2 4
3 2 0];
b = [20;42;30];
lb = zeros(3,1);
Aeq = [];
beq = [];
[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb);4.整数规划(0-1规划) X= intlinprog(f,intcon,A,b),相比于线性规划,多一个intcon输入量。
f = [7 5 9 6 3];
intcon = [1,2,3,4,5];% intcon = [1,2,7]表示x(1),x(2)和x(7)仅取整数值。
A = [56,20,54,42,15;1,4,1,0,0;-1,-2,0,-1,-2];
b = [100;4;-2];
lb = zeros(5,1);
ub = ones(5,1);
[minx,miny,flag] = intlinprog(f,intcon ,A,b,[],[],lb,ub)5.二次规划 X=quadprog(H,f,A,b,Aeq,beq)
H = [1 -1; -1 2];
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];
lb = zeros(2,1);
options = optimoptions('quadprog', 'Algorithm','interior-point-convex','Display','off');
[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb,[],[],options);