信号转换为图像 时域频域分析
一维信号如何转化为图像?深度学习如何学习
1.当然,直接1d卷积也是可以的。
2. 以信号强度的数值作为纵坐标,以时间为横坐标绘制信号点就可以了。
- 直接把多通道的一维信号合并成二维图像,然后直接按图像卷积的方法去做~~
222*5000这样一个图
~可以看看语音处理的相关Net,其中比较推荐的是用 dilated conv 来做 - 按语音识别的套路,先搞时频图。我觉得一维信号预处理有点麻烦,假如待识别信号的范围差距很大,那就蛮难处理。不像图像,灰度图像自身就是0-255的像素点大小范围;而类似振动信号,小的可能很小,大的振动可能也很大,归一化也不好处理。如果用激励层做映射,像tanh和sigmoid 基本都会崩掉,我感觉挺麻烦的,尤其在一维信号无界或者范围过大的情况。所以将其转变为时域频域分析,频域在0.5-35hz
5.或者直接上rnn也行。直接当做是时序数据进行处理
把shape处理好,就不会有计算流程的问题。
https://www.zhihu.com/question/276804048
2, 傅里叶变换
从物理意义上说:这三种变换的本质是将信号从时域转换为频域。傅里叶变换的出现颠覆了人类对世界的认知:世界不仅可以看作时间的变化,也可以看做各种频率不同加权的组合。举个不太恰当的例子:一首钢琴曲的声音波形是时域表达,而它的钢琴谱则是频域表达。
另外,在通信领域,没有信号的频域分析,将很难在时域理解一个信号。因为通信领域中经常需要用频率划分信道,所以一个信号的频域特性要比时域特性重要。
从计算量上面说:三种变换因为可以将微分方程或者差分方程转化为多项式方程,所以大大降低了微分(差分)方程的计算成本。
傅里叶分析包含傅里叶级数与傅里叶变换。傅里叶级数用于对周期信号转换,傅里叶变换用于对非周期信号转换。傅里叶变换要求满足狄利克雷条件和在(﹣∞,+∞)上绝对可积,但绝对可积是一个相当强的条件,很多常见的函数如正弦函数、单位阶跃函数和线性函数都不满足此条件,使这种变换方法少了工程意义,所以就出现了拉氏变换。而z变换则可以算作离散的拉普拉斯变换。
时域分析
世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。 都在随着时间不停的改变,并且永远不会静止下来。
频域,傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。
在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符
但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation)
傅里叶级数的频谱(Fourier Series)
自然界中所有的信号是所有正弦波叠加而成的总和
如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元。
对于我们最常见的有理数轴,数字“1”就是有理数轴的基本单元。
时域的基本单元就是“1秒”,如果我们将一个角频率为\omega_{0} 的正弦波cos(\omega_{0} t)看作基础,那么频域的基本单元就是\omega_{0} 。
有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
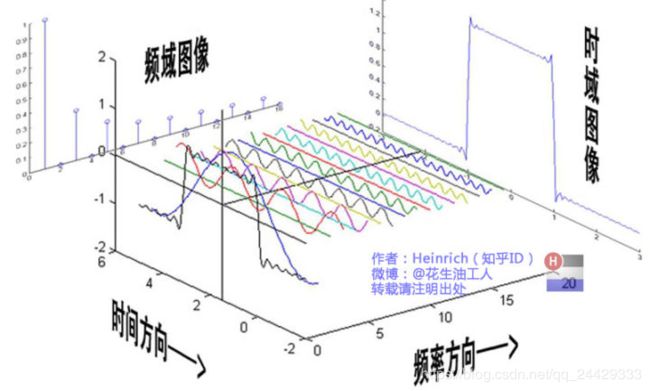
可以发现,在频谱中,偶数项的振幅都是0,也就对应了图中的彩色直线。振幅为0的正弦波
上面是从侧面看,下面是从下面看,主要是相位谱
基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混论,我们用7个波叠加的图。
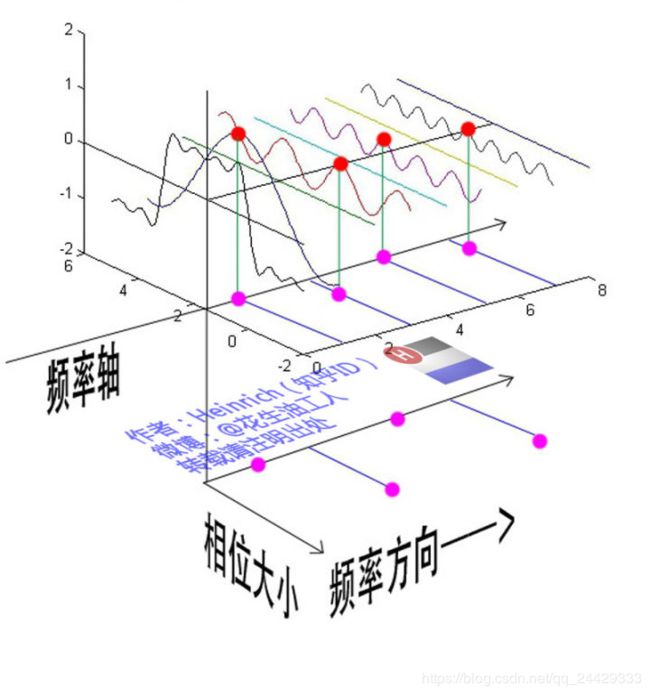
相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi,就得到了相位差。
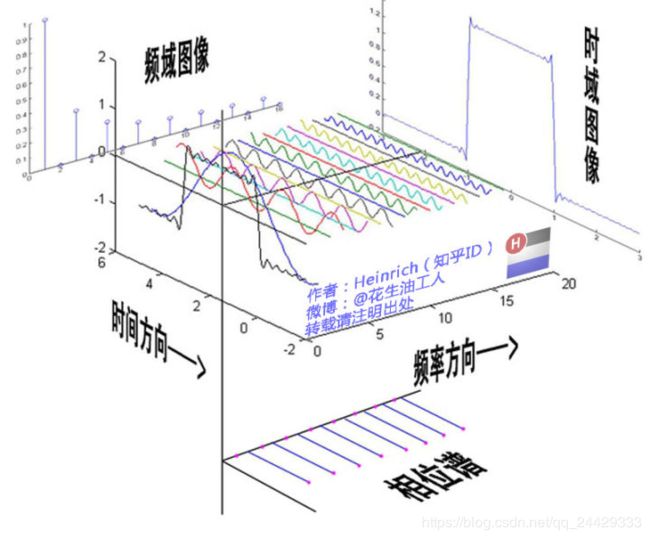
频道。频道频道,就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事:
以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
sin(3x)+sin(5x) 他的频率就是两条竖线 3,5
上面可以看做是周期信号,
傅里叶变换—非周期信号
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。
比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。这句话比较绕嘴,实在看着费事可以干脆回忆第一章的图片。
而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。因此在傅里叶变换在频域上就从离散谱变成了连续谱。原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。

原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
欧拉公式
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1的平方根
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
我们知道乘-1其实就是乘了两次 i使线段旋转了180度,那么乘一次 i 呢——答案很简单——旋转了90度
![]()
这个公式在数学领域的意义要远大于傅里叶分析,但是乘它为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候。
![]()
这个公式关键的作用,是将正弦波统一成了简单的指数形式

欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从0到无穷所有频率的组合。

快速傅里叶变换
FFT(Fast Fourier Transform)快速傅里叶变换是离散傅里叶变换(DFT)的一种快速计算方法。傅里叶分析是将信号从原始域(比如时域)转换到其他域(比如频域)表征的一种方法。而FFT是DFT的一种快速计算方法
x = np.random.random(1024)
np.allclose(DFT_slow(x), np.fft.fft(x))
Numpy内嵌的FFT计算结果做一个对比
https://zhuanlan.zhihu.com/p/23354318
由于在这项工作中使用了二维CNN,因此-
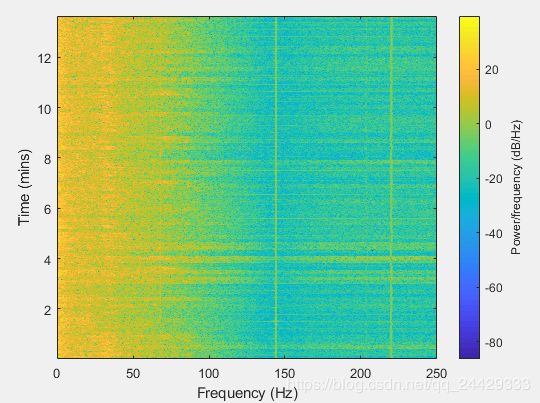
将原始脑电图数据转换成矩阵(如图像格式)的信息。转换必须能够从脑电图信号中保留最重要的信息。小波和傅立叶变换通常用于将时间序列脑电图信号转换为图像形状(Brinkmann等人,2016;Khan、Marcuse、Fields、Swann和Yener,2017)。它们也被用作癫痫检测和预测的有效特征提取方法。在这项工作中,我们使用短时傅立叶变换(STFT)将原始脑电图信号转换成由频率和时间轴组成的二维矩阵。我们使用30 s长的脑电图窗口。大多数脑电图记录都受到50 Hz(见图1a)电源线噪声的污染,而弗赖堡医院数据集和CHB-MIT数据集则为60 Hz。在频域中,通过排除频率范围为47–53 Hz和97–103 Hz的部件(对于50 Hz的电源线频率)和频率范围为57–63 Hz和117–123 Hz的部件(对于60 Hz的电源线频率),可以方便地有效地消除电源线噪声。直流分量(在0赫兹时)也被移除。图1b显示了去除电源线噪声后30秒窗口的STFT。
短时傅里叶变换
原因是因为傅立叶分析有一个非常严重的缺点, 在将信号从时间域变换到频率域去的时候,把时间信息丢失了。 当我们在用傅立叶变化去分析一个具体信号的时候, 我们不知道哪个频率是对应在哪个时间点出现的,在哪个时间点消失的。
如果一个信号的频率并不随着时间变化, 那么我们称它为平稳信号。 那么知道哪一个频率的信号在哪一个时间点出现的就不那么重要了。 可是如果现实生活中我们研究的大多数信号都是非平稳信号,他们都许多非常短暂变化的特性, 这些特点对于我们信号分析的特点, 傅立叶分析并不适合去做这种分析,而短时傅里叶变换则可以。
可见,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
然而平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的,所以在比如生物医学信号分析等领域的论文中,基本看不到单纯傅里叶变换这样naive的方法。
短时傅里叶变换(Short-time Fourier Transform,STFT)–matlab 版本
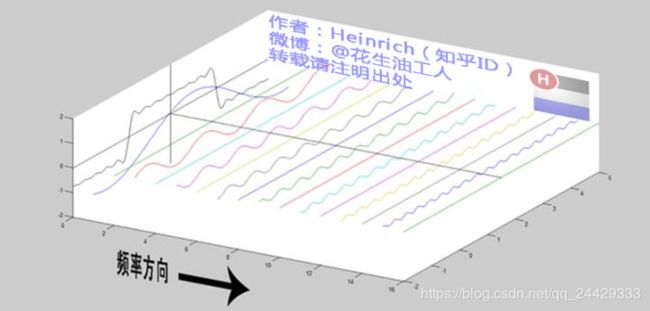
一个简单可行的方法就是——加窗。 “把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
[S,F,T,P]=spectrogram(x,window,noverlap,F,fs)
说明:当使用时无输出参数,会自动绘制频谱图;有输出参数,则会返回输入信号的短时傅里叶变换。当然也可以从函数的返回值S,F,T,P绘制频谱图,具体参见例子。
A=load('E:\I-虚拟机癫痫实验\癫痫实验\0920--小波变换提取\111.txt');
x=A(:,1);%对数据进行选择
fs=500;
N =5000;
nfft=1024;
spectrogram(x,1024,512,nfft,fs);
figure
% 短时傅里叶变换
x—输入信号的向量。默认情况下,即没有后续输入参数,x将被分成8段分别做变换处理,
如果x不能被平分成8段,则会做截断处理。默认情况下,其他参数的默认值为
window—窗函数,默认为nfft长度的海明窗Hamming
noverlap—每一段的重叠样本数,默认值是在各段之间产生50%的重叠
nfft—做FFT变换的长度,默认为256和大于每段长度的最小2次幂之间的最大值。
fs—采样频率,默认值归一化频率 .
Window—窗函数,如果window为一个整数,x将被分成window段,每段使用Hamming窗函数加窗。
如果window是一个向量,x将被分成length(window)段,每一段使用window向量指定的
窗函数加窗。所以如果想获取specgram函数的功能,只需指定一个256长度的Hann窗.