【Graph Embedding】SDNE：深度学习在图嵌入领域的应用

今天学的论文是清华大学崔鹏老师工作《Structural Deep Network Embedding》（后简称 SDNE），并发表于 2016 KDD，目前为止共有 880 多引用，是一个非常经典的将深度学习应用于 NetWork Embedding 的算法。

SDNE 设计了一个由多层非线形函数组成的深度模型来捕捉高度非线性的网络结构，同时联合优化 first-order 和 second-order 学习网络结构，前者用作监督信息以捕捉网络局部结构，后者用作非监督信息以捕捉网络全局结构，所以 SDNE 是一个半监督的深度学习模型。

我相信大家看完这段会有很多疑问，至少我看完有以下疑问：

• 多层非线性函数长什么样子？具有非线性激活函数的多层神经网络？
• 如何把 first-order 用作监督信息？
• 同理，second-order 如何用做非监督学习？
• 如何联合优化？
• 深度模型的 Embedding 怎么出来？还是原来的那个输入矩阵吗？
• 引入深度模型是为了拟合高度非线形的网络，那速度怎么样？可以用于大规模网络吗？

带着问题，我们来一起读一下论文。

1. Introduction

在真实网络世界中学习 NetWork Embedding，有三大挑战：

• 高度非线性：网络的底层结构是高度非线性的，使用浅层网络无法捕捉高度非线性的网络结构；
• 结构捕捉：既要捕捉网络的局部结构，又要捕捉网络的全局结构；
• 稀疏性：大部分真实网络都是稀疏的，仅利用节点的有限连接是不够的。

为了解决这三大问题，作者也提出了三大解决方案：

• 高度非线性：设计了一个由多层非线性函数组成的深度网络来学习 NetWork Embedding，深度网络有强大的表示能力来学习网络的复杂结构；而多层非线性函数可以将数据映射到一个高度非线性的潜在空间，可以更好的捕捉到高度非线性的网络结构；
• 结构捕捉：将 first-order 和 second-order 联合应用到网络的学习过程中，前者用于捕捉网络局部结构，后者用于捕捉网络全局结构；
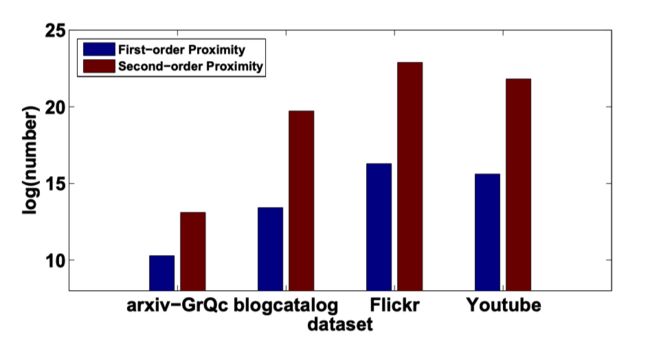
• 稀疏性：first-order 是基于节点间的边连接，即原始网络结构；而 second-order 是基于两个节点共享的邻域连接来捕捉节点的相似性，且具有 second-order 相似性的节点数量更多，如下图所示，所以加入 second-order 一定程度上缓解了网络稀疏的问题。

2. SDNE

我们来看下 SDNE 具体是怎么实现的。

2.1 Autoencoder

在介绍 SDNE 的整体框架前，我们先补充学习一个基础知识——自编码器。

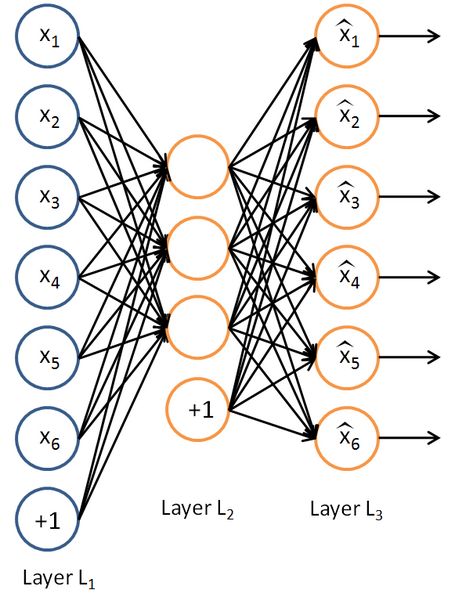
自编码器（AutoEncoder） 是只有一层隐层节点，输入和输出具有相同节点数的神经网络，其目的是求函数：$f(x) \approx x $。简单放一张图：

可以看到，不考虑输入层偏置项的话，输入节点和输出节点是一致的。那么我们为什么要这么做呢？

举一个例子：我们传输大文件时有两种方式——直接传和压缩后再传。我们通常会选择后者，因为压缩后不但文件的体积会变小，还足以通过解压还原出原来的文件。

而自动编码器也类似于这种过程，为了尽可能复现输入数据，自编码器必须捕捉输入数据的重要特征，从而找到能够代表原数据的主要成分，这个过程有点类似主成分分析（Principal Components Analysis，PCA）。

自编码器没有标签数据，所以是一种非监督学习，前半部分为编码器，后半部分为解码器。在实际应用中通常会使用自编码器的前半部分。

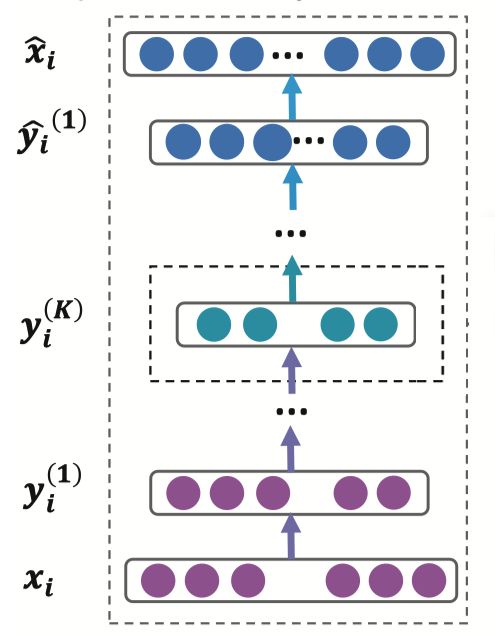
SDNE 采用的自编码器比较深，有多个隐藏层，如下图所示：

自编码器的隐藏层可以表示为：
$$\begin{array}{rl}{y}_i^{(1)}& =\sigma (W^{(1)}{x}_i+b^{(1)})\\ y_i^{(k)}& =\sigma (W^{(k)}{y}_i^{(k-1)}+b^{(k)}),k=2,...,K\end{array}$$
其中，$x_i$ 为输入值，$y_i^{(k)}$ 为第 k 层的 i 个节点的输出值，$W^{(k)}$ 为第 k 层的参数矩阵，$b^{(k)}$ 为第 k 层的偏置项。

得到 $y_i^{(K)}$ 后，我们通过反转编码器的计算过程得到输出值 ${\hat{x}}_i$，自编码器的目标是最小化输入和输出的重构误差，所以代价函数为：
$$L=\sum _{i=1}^n{||{\hat{x}}_i-x_i||}_2^2$$

2.2 FrameWork

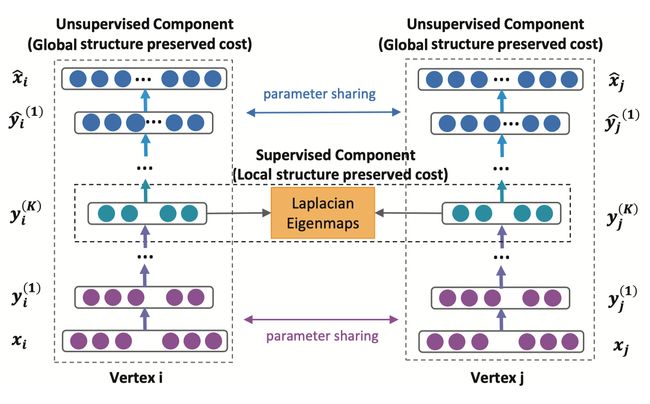
然后我们来看下 SDNE 的整体框架：

以左边的为例：输入为邻接矩阵，输出为重构后的邻接矩阵，通过优化重构误差来捕捉全局结构特征；而中间一排，$y_i^{(K)}$ 就是我们需要的 Embedding 向量，模型通过拉普拉斯特征特征映射（Laplacian Eigenmaps）优化的代价函数使得相邻节点的 Embedding 向量距离更近，从而捕捉节点的局部特征。

PS：个人猜测：这里框架图虽然画了两个自编码器，SDNE 应该是只有一个自编码器。如果是两个的话，共享参数这个操作过于复杂，而记录邻居节点的 Embedding 向量就比较容易了。

2.3 Object Functions

再来看一下半监督模型的目标函数，目标函数由代价函数和正则项构成，SDNE 的代价函数分为两块，一块是 first-order ，另一块是 second-order 。

我们先来看一下如何在代价函数中加入 second-order 来捕捉全局网络结构。

second-order 是基于节点的邻域建模的，所以我们定义邻接矩阵：
$$\begin{gathered} S=\{s_1,s_2,...,s_n\} \\ {s}_i=\{s_{ij}{\}}_{j=1}^n,s_{ij}>0 \end{gathered}$$
其中，$s_{ij}$ 为节点$v_i$ 和节点 $v_j$ 之间的边，这里考虑加权边；$s_i$ 描述了节点 $v_i$ 的的邻域结构。

我们将 $s_i$ 作为自编码器的输入，即 $x_i=s_i$ ，由于 $s_i$ 反映了节点 $v_i$ 的邻域结构，所以通过自编码器的重构可以使得具有类似特征的节点获得相似的 Embedding 向量。

然而，由于网络的稀疏性，$s_i$ 将有大量的非零元素，所以如果直接使用 S 作为自编码器的输入则可能会重构出 S 的零元素。所以为了解决这问题，我们加大了非零元素的惩罚权重，修正后的代价函数为：
$$\begin{array}{rl}{l}_{2nd}& =\sum _{i=1}^n{||({\hat{x}}_i-x_i)\odot b_i||}_2^2\\ & ={||\hat{X}-X||}_F^2\end{array}$$
其中，$\odot$ 表示哈达玛积（Hadamard product），类似于向量的内积；$b_i=\{b_{ij}{\}}_{j=1}^n$ ，当 $s_{ij}=0$ 时，$b_{ij}=1$，否则 $b_{ij} = \beta >1 $。

Hadamard product：设 $A=[a_{ij}{]}_{(m,n)}$ $B=[b_{ij}{]}_{(m,n)}$ ，则 $A \odot B = [a_{ij} \cdot b_{ij}]_{(m,n)} \$

通过修正后的自编码器，以邻接矩阵 S 为输入，以最小化重构误差为约束，可以将具有相似邻域结构节点的 Embedding 向量映射到相邻位置，即通过 Second-order 捕捉了网络的全局结构。

同样的，既要捕捉网络的全局结构，也要保证网络的局部结构。

我们以 first-order 表示网络的局部结构，使得有连接边的节点 Embedding 向量相近，所以代价函数为：
$$\begin{array}{rl}{l}_{1st}& =\sum _{i,j=1}^n{s}_{ij}{||y_i^{(K)}-y_j^{(K)}||}_2^2\\ & =\sum _{i,j=1}^n{s}_{ij}{||y_i-y_j||}_2^2\end{array}$$
为了保证 first-order 和 second-order 相似性，我们将代价函数联合起来，加上正则项后便得到目标函数：
$$L_{mix}=L_{2nd}+\alpha L_{1st}+\nu L_{reg}$$
其中，$\alpha ,\nu$ 为超参，$L_{reg}$ 为正则项：
$$L_{reg}=\frac{1}{2}\sum _{k=1}^K({||W^{(k)}||}_F^2+{||{\hat{W}}^{(k)}||}_F^2)$$

2.4 Optimization

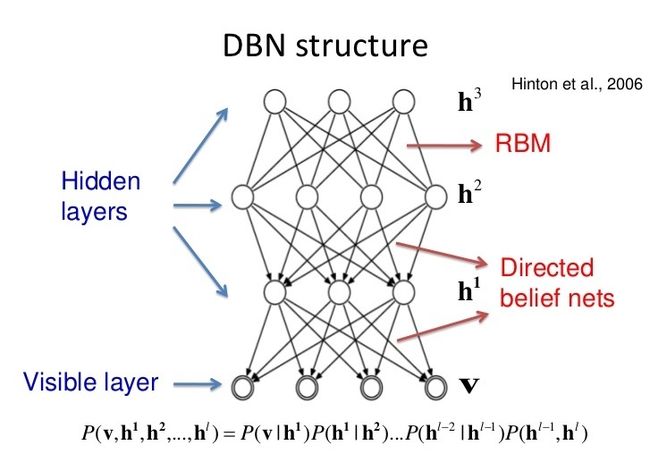
SDNE 使用反向传播来更新网络参数，但由于模型高度非线性，参数空间中可能存在许多局部最优。因此，为了得到全局最优，作者使用深度信念网络（Deep Belief Network，以下简称 DBN）对参数进行预训练。

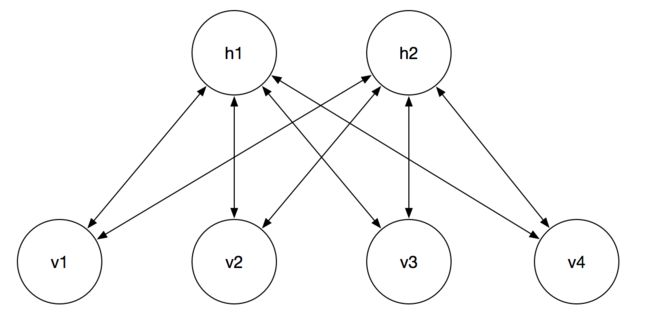
简单介绍一下 DBN，DBN 是由 HInton 大佬在 2006 年提出的一个概率生成模型，其由多个 RBM 组成。所以在介绍 DBN 之前我们先来介绍下受限玻尔兹曼机（Restricted Boltzmann Machines，以下简称 RBM），下图 RBM 的结构图：

其中，$V=(v_1,v_2,...,v_{|V|}{)}^T$ 层显层的状态向量，$H=(h_1,h_2,...h_{|H|}{)}^T$ 层为隐藏层的状态向量，两层之间的权重为 $W=[w_{ij}{]}_{(|H|,|V|)}$，每个神经元都有自己的一个偏置项，对隐层而言偏置项为 $B=[b_j{]}_{(|H|,1)}$，对显层而言偏置项为 $C=[c_j{]}_{(|V|,1)}$。

在 RBM 中，隐层被激活的概率为：
$$p(h_j|V)=\sigma (\sum _i{w}_{ij}{x}_i+b_j)$$
由于是双向连接，所以显层也同样可以被激活：
$$p(v_j|H)=\sigma (\sum _i{w}_{ij}{h}_i+c_i)$$
以上就是 RBM 的基本构造过程，并不复杂， 我们来看下工作原理：

当一条数据输入到显层时，RBM 会根据公式计算出每个隐层被开启的概率，并通过阈值来判定是否被激活：
$$h_j=\{\begin{array}{rl}& 1ifp(h_j|x)\ge \mu \\ & 0otherwise\end{array}$$
由此便可以得到隐层的每个神经元是否被激活，给定隐层时，显层的计算方式一致。

了解了工作原理后，我们来看下 RBM 的训练方式：

1. 给定的一条数据赋值给显层 $V$，并计算出隐层每个神经元被激活的概率 $p(h_j|V)$ ；
2. 对计算的概率分布进行 Gibbs 采样计算隐层的输出值：$h_i \sim P(h_i|V) $；
3. 利用隐层的状态向量重构显层，即通过 $H$ 层推导出 $V$ ，可以计算出显层的每个神经元被激活的概率 $p(v_i|H)$；
4. 同样利用 Gibbs 采样计算显层重构值：$\hat{v}\sim p(v_i|H)$；
5. 重构值和原本的输入值的误差比较大，所以需要利用反向传播去更新权重以缩小误差；
6. 重复迭代，直到达到终止条件。

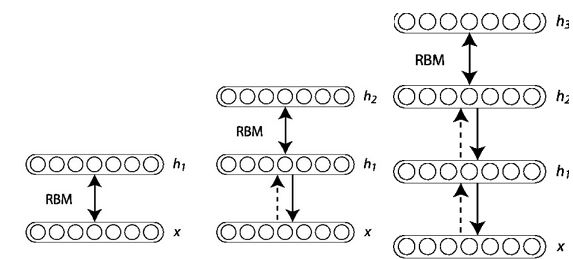
DBN 可以视为由多个 RBM 串联起来的结构，下图为最终训练得到的模型：

在训练时最下面为第一层结构，相邻两层构成一个 RBM，必须充分训练 RBM 后才能训练下一个 RBM，训练过程如下图所示：

DBM 是深度学习训练中非常有效的参数初始化方法。

我们现在回过头来简要的看下 SDNE 的算法：

2.5 Analysis

这一节主要分析一下新节点的 Embedding 和训练复杂度：

• 新节点：如果新节点 $v_k$ 与现有节点有连接，那么有连接向量：$s_k=\{s_{1k},s_{2k},...,s_{nk}\}$ ，可以利用已有的模型去训练得到新节点的 Embedding 向量，时间复杂度为 $O(1)$；如果没有连接，那目前的工作就没办法了～；
• 时间复杂度：时间复杂度为 $O(ncdI)$ ，其中 n 为节点数量，d 为隐藏层最大维度数，c 为网络的平均度数，I 为迭代次数。

3. Experiments

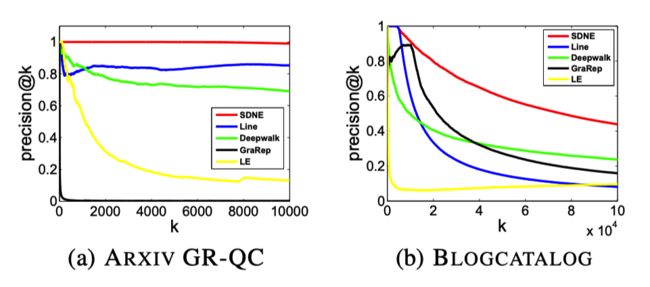
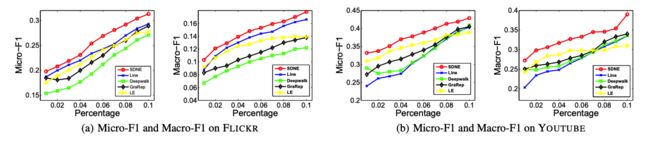
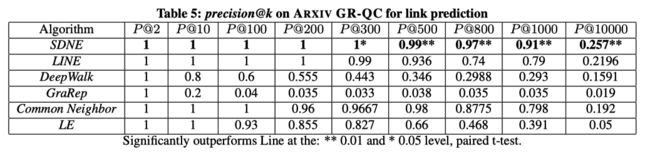
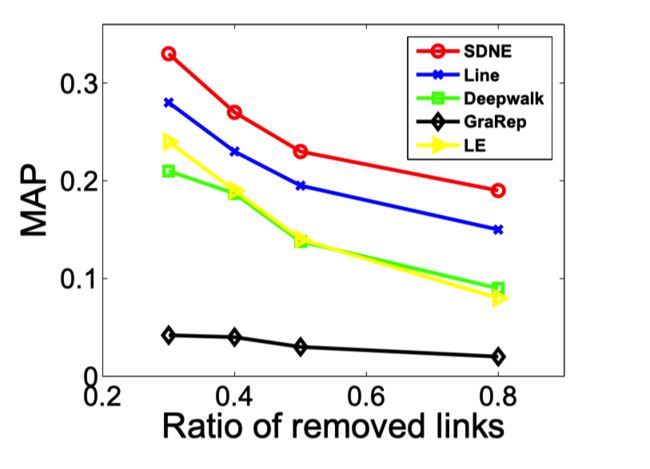
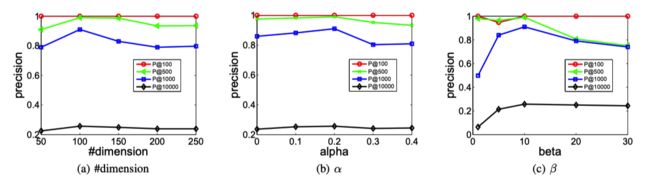
我们来看一下 SDNE 在不同数据集下，采用不同评价指标（MAP、Precision）的性能表现：

SDNE 在多标签分类任务中的表现：

SDNE 在边预测任务中的表现：

SDNE 在不同稀疏程度的数据集中的表现：

SDNE 的可视化：

SDNE 的参数敏感性：

4. Conclusion

一句话总结：SDNE 是一个具有多层非线性函数的半监督深度学习模型，其利用 first-order 和 second-order 分别捕捉网络的局部结构和全局结构，使得训练出来的 Embedding 更具鲁棒性，并在多个真实数据集中获得良好的表现。

论文到此就结束了，回答一部分看完摘要时提出的疑问：

• 深度模型的 Embedding 还是原来的那个输入矩阵吗？

  先讨论这个问题，Embedding 应该是 SDNE 中间 $y^{(K)}$ 层的输出值，对于每一个节点其经过多层非线性网络后多会有不同的输出值。

• first-order 如何用作监督信息？second-order 又如何用作非监督学习？如何联合优化？

  我是这样理解的：

  • second-order 其代价函数是输入的共现矩阵和重构的共现矩阵的误差，属于非监督学习；
  • 而 first-order 的代价函数是节点的 Embedding 向量与邻居节点的 Embedding 向量的误差，对于当前节点而言，其 Label 是邻居节点，所以属于监督学习；
  • 联合优化是指，把两个代价函数放在一起计算总体误差，区别于分开训练（还记得哪个模型是分开训练的吗？）。

• 引入深度模型是为了拟合高度非线形的网络，那速度怎么样？可以用于大规模网络吗？

  论文没写，大概率速度会很慢，虽然论文时间复杂度为 $O(ncdI)$ ，每一轮迭代的时间复杂度与节点数量成线性关系，但我觉得有两个 Bug：

  • 论文中指出 d 为隐层最大维度数（d is the maximum dimension of the hidden layer），但我觉得应该算成 sum 而不是 max，当然也要考虑是否采用 Negative Sampling、Dropout 等优化方式；
  • SDNE 需要 DBN 进行预训练，这个时间也应该加上去，虽然 DBN 的预训练会加速 SDNE 的收敛，DBN 本身训练过程就比较慢；

  但 Embedding 通常是离线操作，如果其训练时间可以接受，也不一定非要非常快的速度。

5. Reference

1. 《Structural Deep Network Embedding》
2. 《深度学习之autoencoder》
3. Upadhyay, Rishabh. (2017). Accent Classification Using Deep Belief Network.
4. 《深度学习读书笔记之RBM（限制波尔兹曼机）》

关注公众号跟踪最新内容：阿泽的学习笔记。