动态规划7:最优编辑练习题
题目:对于两个字符串A和B,我们需要进行插入、删除和修改操作将A串变为B串,定义c0,c1,c2分别为三种操作的代价,请设计一个高效算法,求出将A串变为B串所需要的最少代价。给定两个字符串A和B,及它们的长度和三种操作代价,请返回将A串变为B串所需要的最小代价。保证两串长度均小于等于300,且三种代价值均小于等于100。
测试样例:"abc",3,"adc",3,5,3,100返回:8
思路:这种题目如果不使用动态规划基本无从着手,难度很大,时间复杂度很高,因此在思考时就应该从动态规划的角度去思考问题,动态规划有4部曲,逐步解决即可。对于这种能够将问题拆分成为2个维度的问题(A串作为纵向,B串作为横向),通常就是使用动态规划建立二维数组来进行解决。在建立二维数组时要注意是建立n*m的矩阵还是建立(n+1)*(m+1)的矩阵,关键是思考对于数组为””空串的情形是否要作为初始条件,即是否应该让空串作为初始条件,从实际意义上来理解,空串也是一种字符串,且与可能要求将空串编辑成为某个字符串,或者将某个字符串编辑成为空串,因此需要对字符串A,B从空串“”开始进行拆分考虑。但是实际上是否从空串或者0开始分解要看如果分解成为这种初始条件是否可以据此求出后面的所有情况的结果,即所求的第1行,第1列应当是有效的,能够据此求出后面的一系列情况,而不是固定的记住。
找零钱问题:
使用0~i种零钱凑出j,这里i从0即第1个数开始,j从0开始到aim共有aim+1个数值,之所以要从0考虑并且将使用0~i凑出j的值都记为1(其实这没有实际意义)是为了让之后的dp[i][j]计算时利用1恰好能够得到所需的结果,因此并不是先确定了1再求结果而是根据结果需要将这一列放到dp数组中并令其为1,其实这里1的本质是递归条件的边界条件,怎样算作一种方法呢?当aim=0时表示拼凑结束于是当前的零钱0~i算作一种方案。也可以记住,零钱问题是一个典型的动态规划问题,应该记住。
台阶问题:
f(n)=f(n-1)+f(n-2);
先求边界初始值,f(1)=1表示上1级台阶有1中方法;f(2)=2表示上2级台阶有2种方法,那么f(0)是否需要呢?如果需要值应该为几呢?根据需要来思考,为了使得f(2)=f(1)+f(0)成立,得出f(0)应该等于1,即上0级台阶的方法数目是1,这其实没有什么实际意义,仅仅从需要出发,对于每次跳1或2级的简单台阶问题,台阶数是否从0开始考虑都没有关系,但是对于变态台阶问题,每次可以跳的数目是arr[0~i],那么必须建立二维dp[][]矩阵才能解决,等价于零钱凑整问题。因此为了使得dp[][]可以递推求得,必须先计算出j=0时的dp[][]的值。
矩阵最小路径和问题:
这里行i和列j是已经给定的i和j是离散值不是连续值,同时第1行和第1列的值容易求出,之后的dp[i][j]可以根据第1行和第1列的值求出,因此建立的dp[][]矩阵是n*m

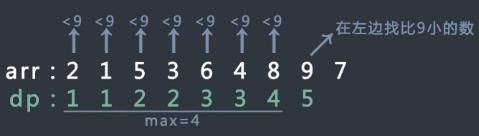
LIS最长递增子序列问题:
给定的需要研究的是一个数组的最长递增子序列,对于数组显然只能从第1个元素,即i=0开始进行研究和分解,不像零钱问题中的零钱需要考虑凑出0元的情况和台阶问题中需要考虑上0级台阶的情况。
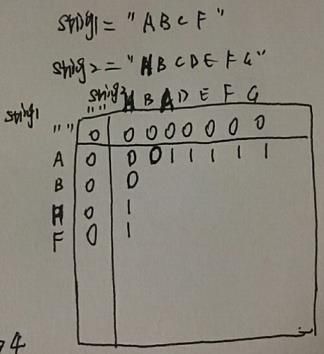
LCS最长公共子序列问题:
给定的是2个字符串,求最长公共子序列,按照前面的经验应该从空串开始考虑,即先求String1空串与String2前j个字符的公共子序列长度,再求String空串与String1前i个字符的公共子序列长度,但是分析发现此时第1行和第1列都是0,显然无法据此推出之后的dp[][],因此还是需要计算第2行和第2列,因此一开始建立dp[][]的时候就不应该考虑String1和String2为空串的情况,即是否考虑最基础的空串或者aim=0作为第1行和第1列没有固定规律可循,关键是看以谁作为第1行第1列可以递推出后面的所有dp[][]值以及此时的第1行第1列是否容易求出(动态规划中的第1行和第1列总是可以很简单的直接求出且不依赖于前面的结果,如果计算时还需要依赖前面的结果那么必然不是最初始的情况)01背包练习题:
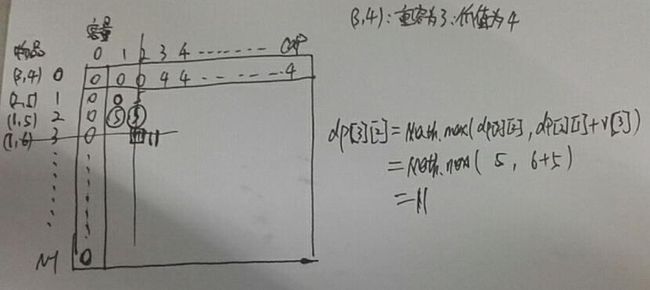
本题中重量j是一个连续值,按照前面的经验,应该从j=0开始考虑到cap共cap+1个值,先求出第1行和第1列,发现第1列全部是0,发现这1列其实是没有意义的,无法据此推出后面的结果,那么应该计算第2列作为初始值,但是这里特殊的,发现对于任意dp[i][j]它仅仅依赖于上一层的数据而不依赖于本层左边的数据,因此只需要求出第1行的基础数据,之后就可以递推求处所有的数据了。但是为了统一,还是将j从0开始考虑。最优编辑问题:
本题给定2个字符串A,B求将A转换为B的最小代价,无论从经验还是从实际意义上来考虑都需要从空串进行考虑,于是应该创建一个(n+1)(m+1)的dp[][]矩阵。

先计算第1行和第1列的结果,对于第1行,就是要将空串“”转变为“”或者str2的前j个字符串,转换方式有很多种,可以删删改改增增减减,但是代价最小的方式一定是逐个插入元素,于是,第一行的dp值就是插入j个元素所需要的代价,即dp[0][j]=ic*j;同理对于第1列表示从str1的前i个元素字符串转变为空串,最小代价一定是逐个删除元素,于是对于第一列,dp[i][0]=dc*i;此外,对于任何位置dp[i][j]表示用字符串str1中0~i-1的字符串来转换为str2中0~j-1的字符串,此时的最小代价只可能来自4种情况:其实在动态规划中是为了利用前面已经计算得到的结果而去找出当前所求的dp[i][j]与之前已经求出的dp[i-1][j]或者dp[i][j-1]或者dp[i-1][j-1]的关系,即是主动的去找可能可以得出结果的情况,然后想办法将其转变为当前所求的值,可以直接有前面的值得到当前值,也可以找几个可能可以推出当前所求值的情况作比较得出当前值。
情况1:对于dp[i][j]例如上图中要将“ab12c”转变为“abcd”,可以先将“ab12c”删除最后一个字符c得到“ab12”,然后将“ab12”转变为“abcd”,由于“ab12”转变为“abcd”的最小代价已知是dp[i-1][j],于是此时的最小代价是dp[i-1][j]+c1;
情况2:可以先将“ab12c”转变为“abc”即最小代价为dp[i][j-1],然后再插入最后一个元素d,此时的最小代价为dp[i][j-1]+c0;
情况3:如果2个要转换的字符串最后一个元素不同,即str1[i-1]!=str2[j-1],那么还可以先将“ab12”转变为“abc”,然后将最后一个元素进行替换,即从c替换为d,此时的最小代价为dp[i-1][j-1]+c2;
情况4:当2个要转换的字符串的最后一个元素相同是,即str1[i-1]==str2[j-1],那么此时的最小代价就是不用动最后一个元素,将前面的2个字符串进行转换的最小代价,即为dp[i-1][j-1].
理解:对于dp[i][j]的最小值,它必然来自于上面4中情况之一,不可能有其他情况,即思考时按照转变时最后一个步骤的操作的情况来划分的,最后一个步骤只能是插入、删除或者替换。
动态规划4部曲:
①创建动态规划二维数组存放答案dp[n+1][m+1];
②计算第1行和第1列的结果
第1行:
dp[0][j]=c0*j;
第1列:
dp[i][0]=c1*i;
③从上到下,从左到右计算任意dp[i][j],按照str1[i-1]==str[j-1]是否成立来分开考虑
If(str1[i-1]==str[j-1])dp[i][j]=dp[i-1][j-1]
If(str1[i-1]!=str[j-1])dp[i][j]=Math.min(Math.min(dp[i][j-1]+c0,dp[i-1][j]+c1),dp[i-1][j-1]+c2);
④返回结果,矩阵右下角的值就是结果dp[n][m];import java.util.*;
//最优编辑问题:动态规划
public class MinCost {
public int findMinCost(String A, int n, String B, int m, int c0, int c1, int c2) {
//特殊输入
if(A==null||B==null||n<0||m<0) return 0;
//先将字符串转变为数组才能进行操作
char[] arrA=A.toCharArray();
char[] arrB=B.toCharArray();
//①创建二维数组存放结果dp[][]
int[][]dp=new int[n+1][m+1];
//②计算第1行的结果
for(int j=0;j<=m;j++){
dp[0][j]=c0*j;
}
//②计算第1列的结果
for(int i=0;i<=n;i++){
dp[i][0]=c1*i;
}
//③从上到下,从左到右计算任意位置dp[][]
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(arrA[i-1]==arrB[j-1]){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(Math.min(dp[i-1][j]+c1,dp[i][j-1]+c0),dp[i-1][j-1]+c2);
}
}
}
//④返回结果,即右下角的值
return dp[n][m];
}
}