Balanced Binary Neural Networks With Gated Residual

文章链接

motivation

目前的二值化方法与全精度模型的精度差距比较大。作者认为是因为二值网络中的信息在传播的时候，很多都丢失了。为了解决这个问题，作者提出了Balanced Binary Network with Gated Residual(BBG)

Method

Maximizing Entropy with Balanced Binary Weights

对于二值网络引起的信息丢失的问题，作者提出maximize entropy of binary weight in the training process，即最大化训练过程中权重的"熵"。在信息论中的“熵”，表示消除不确定因素所需要的信息量，“熵”越小，信息越确定。但是作者想要“熵”越大，就是说它表示的信息越不确定，即可能会表达出很多种信息，潜在的表达能力越高。在2020年的CVPR论文《Forward and Backward Information Retention for Accurate Binary Neural Networks》也有类似的观点。
但是作者并不直接优化“熵”这个正则项，转而约束二值权重的期望值为0。具体做法为，对于一个实值权重$v\in {\mathbb{R}}^{d\times d}$，先减去自身的均值，使得实值权重是中心对称的：
$$w=v-\frac{1}{d}1(1^{T}v)$$
这个过程称为balanced weight normalization。然后量化balance之后的$w$:
$$Forward:w^b=sign(w)\times E(\left|w\right|)$$$$Backward:\frac{\partial L}{\partial w^b}=\frac{\partial L}{\partial w}$$
这一套下来就叫做balanced weight quantization。具体的图示如下图

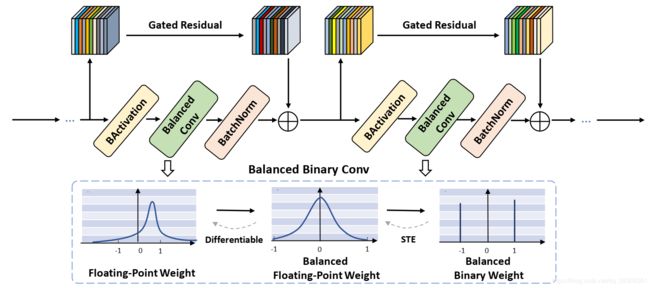
Reconstructing Information Flow with Gated Residual

对激活值的量化方法，如下所示：
$$Forward:x^b=round(clip(x,0,1))$$$$Backward:\frac{\partial L}{\partial x^b}=\frac{\partial L}{\partial w}{\mathbb{I}}_{0<x<1}$$
其中，${\mathbb{I}}_{0<x<1}$表示当$0<x<1$时，它为1，否则为0。
由于这种量化方法丢失了很多的信息，作者提出了一个新的module，叫做gated residual，在前向过程中来逐通道地重构信息。Gated residual employs the floating-point activations to reduce quantization error and recalibrate features。具体做法为：使用一个类似ResNet中的shortcut，只不过将shortcut替换成一个layer，其权重为$s=[s_1,\cdots ,s_c]\in {\mathbb{R}}^c$，这个权重是为了学习浮点的输入特征图的channel级的attention information，这个层对于第$i$个输入通道的操作为：$$r({\text{x}}_i,s_i)=s_i{\text{x}}_i$$yo由于加上了浮点的激活值，输出特征出的表达能力得到了增强。Gated module的输出为：$$y=F(\text{x})+r(\text{x},s)$$其中$F(\text{x})$表示主路的输出，即包含activation binarization, balanced convolution 和BatchNorm的那一路。
这个Gated module带来的好处，就类似ResNet里面的shortcut的好处。具体可参见源论文。

Experiment

在实验的时候，作者没有量化第一层和最后一层，也没有量化downsample层。在分类和检测上均进行了实验，SSD中只量化了backbone，结果如下表。

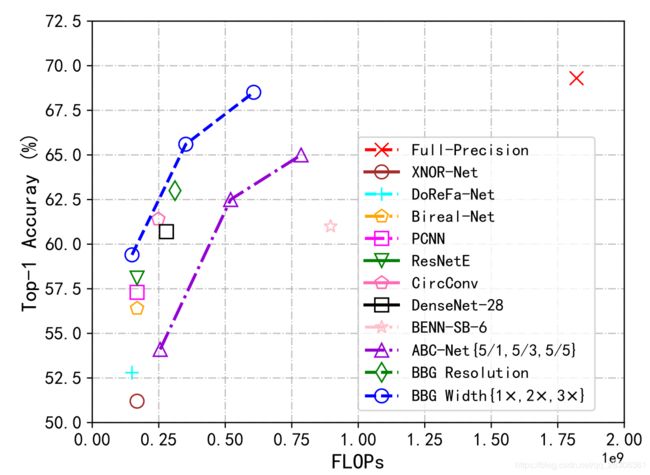
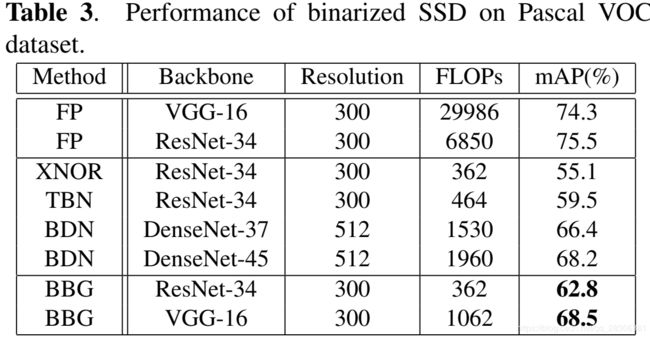
Summary

个人感觉文章的实现不会很难，gated layer的作者肯定是可以提精度的，但是这就说明网络的参数并没有全部量化掉，消融实验是在CIFAR上面做的，不知道在ImageNet上的效果如何，只能说可以借鉴参考一下。首尾层全都量化具体效果需要实践才能验证。不过思路还是可以借鉴一下滴~