【Leetcode】二叉树问题整理笔记
Overview
- 二叉树节点类实现
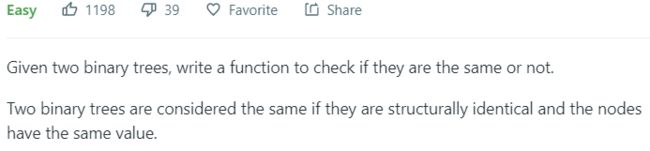
- 100. Same Tree - 判断给定两棵二叉树是否“相等”
- 按层遍历算法问题
- 简单的队列实现
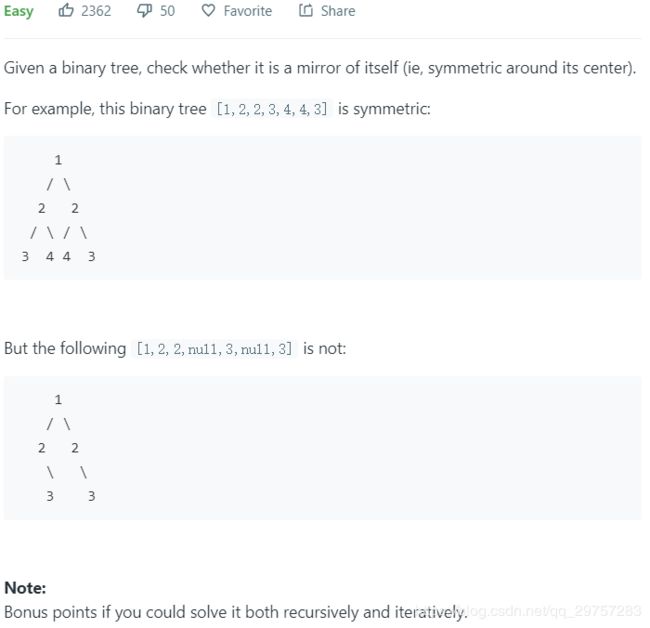
- 101. Symmetric Tree - 判断二叉树是否对称
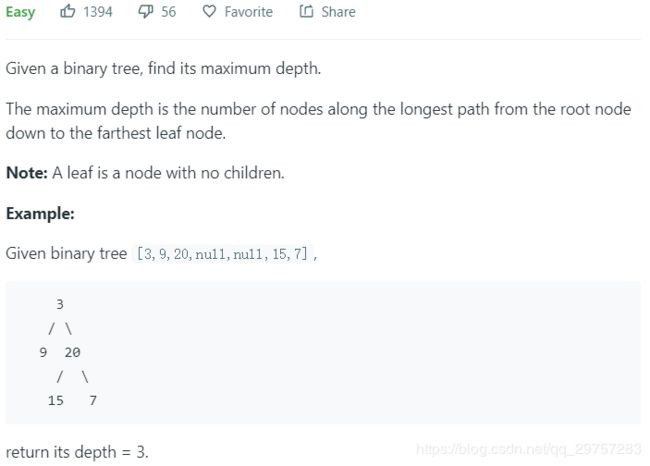
- 104. Maximum Depth of Binary Tree - 求二叉树的最大深度
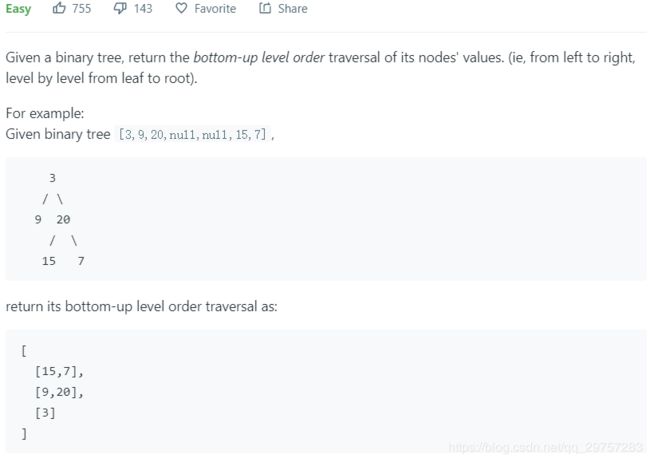
- 107. Binary Tree Level Order Traversal II - 二叉树按层逆遍历
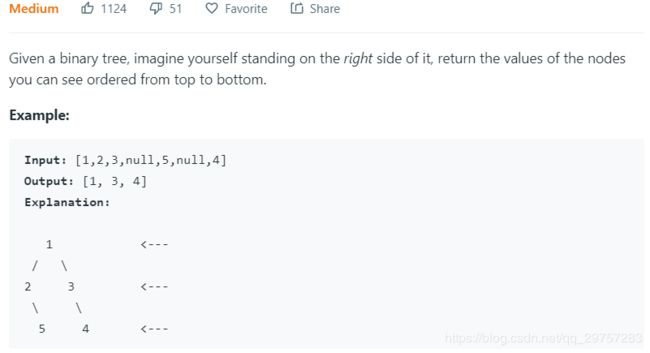
- 199. Binary Tree Right Side View - 获取二叉树的所有最右节点
- 102. Binary Tree Level Order Traversal - 二叉树按层遍历
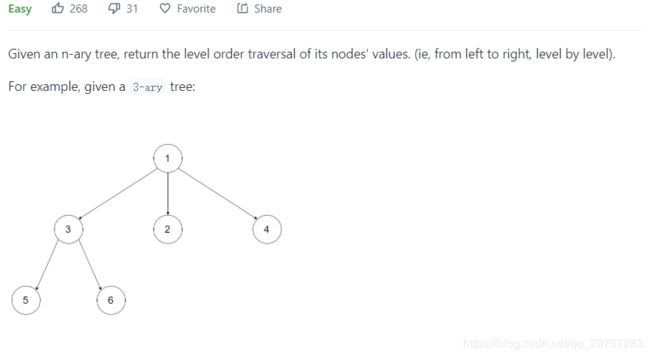
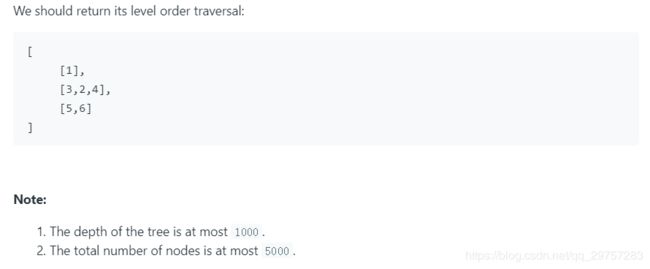
- 429. N-ary Tree Level Order Traversal - N-ary 树按层遍历
- 559. Maximum Depth of N-ary Tree
- 637. Average of Levels in Binary Tree - 获取二叉树每一层的平均值
- 构建(整棵)二叉树
- 108. Convert Sorted Array to Binary Search Tree
- 109. Convert Sorted List to Binary Search Tree
- 公共祖先问题
- 235. Lowest Common Ancestor of a Binary Search Tree
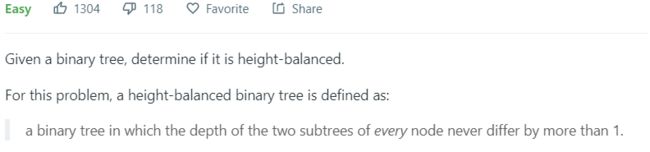
- 110. Balanced Binary Tree - 判断二叉树是否平衡
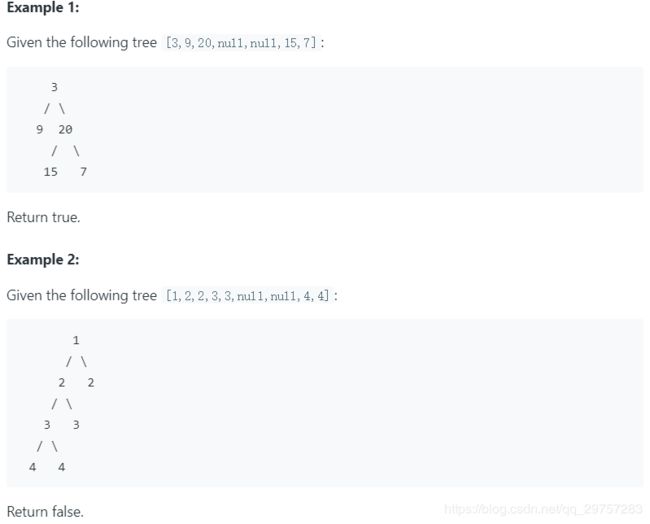
- 112. Path Sum - 判断二叉树是否存在一条根到叶的路径使和为指定值
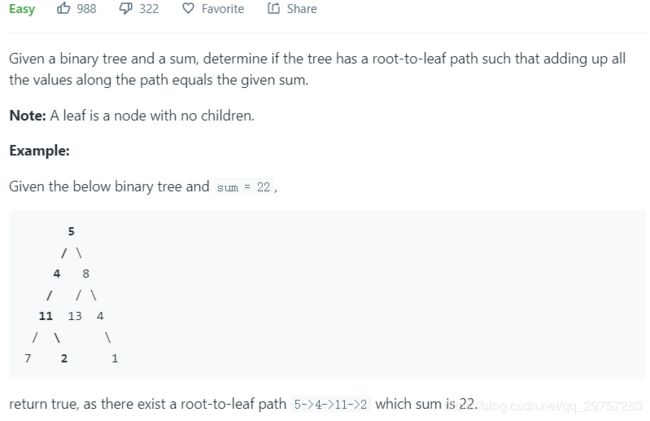
- 226. Invert Binary Tree -- 翻转二叉树
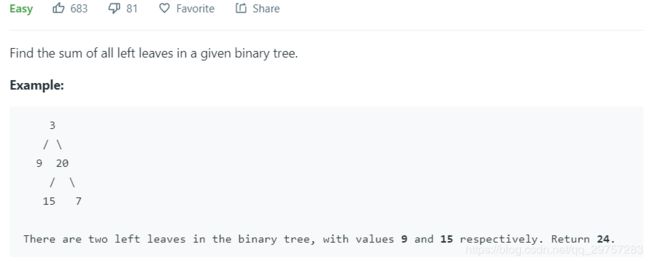
- 404. Sum of Left Leaves
- 572. Subtree of Another Tree - 判断一棵二叉树是否是另一个二叉树的子树
- Reference
二叉树节点类实现
# Definition for a binary tree node.
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
100. Same Tree - 判断给定两棵二叉树是否“相等”
可以使用递归实现。能用递归解决的问题,实现起来会简单很多!
class Solution:
def is_same_tree(self, p, q):
if p is None or q is None:
if p is None and q is None:
return True
else:
return False
if p.val == q.val:
if self.is_same_tree(p.left, q.left):
if self.is_same_tree(p.right, q.right):
return True
else:
return False
else:
return False
else:
return False
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
return self.is_same_tree(p, q)
按层遍历算法问题
简单的队列实现
class DQ:
def __init__(self, val):
self._dq = [val]
def pop_left(self):
return self._dq.pop(0)
def append(self, val):
self._dq.append(val)
def is_empty(self):
return len(self._dq) == 0
def __len__(self):
return len(self._dq)
101. Symmetric Tree - 判断二叉树是否对称
Solution:
提示有递归的实现方法。确实没有想到。这里是迭代的方式。
class Solution:
def is_symmetric_list(self, node_list):
_len = len(node_list)
if _len % 2 == 1:
return False
else:
half = _len // 2
for i in range(half):
if node_list[i] is None and node_list[-i-1] is None:
pass
elif node_list[i] is not None and node_list[-i-1] is not None:
if node_list[i].val == node_list[-i-1].val:
pass
else:
return False
else:
return False
return True
def is_symmetric(self, root):
if root is None:
return True
dq = DQ(root)
node = dq.pop_left()
dq.append(node.left)
dq.append(node.right)
while not dq.is_empty():
cmp = list()
for _ in range(len(dq)):
node = dq.pop_left()
cmp.append(node)
if not self.is_symmetric_list(cmp):
return False
for node in cmp:
if node is not None:
dq.append(node.left)
dq.append(node.right)
return True
def isSymmetric(self, root: TreeNode) -> bool:
return self.is_symmetric(root)
104. Maximum Depth of Binary Tree - 求二叉树的最大深度
Solution:
这里的代码和 101 实际上非常相似。只不过不需要判断当前层的值是否是对称的,以及不将为 None 的子树加入队列。
class Solution:
def get_max_deepth(self, root):
dq = DQ(root)
deepth = 0
while not dq.is_empty():
deepth += 1
level = list()
for _ in range(len(dq)):
level.append(dq.pop_left())
for node in level:
if node is not None:
if node.left is not None:
dq.append(node.left)
if node.right is not None:
dq.append(node.right)
return deepth
def maxDepth(self, root: TreeNode) -> int:
if root is None:
return 0
return self.get_max_deepth(root)
107. Binary Tree Level Order Traversal II - 二叉树按层逆遍历
Solution:
当然了,这个问题按层遍历的意图更加明显。
不过原来我倒是不大想得到按层遍历除了使用队列之外,还能如何使用递归实现。
但是在考虑这个问题的时候,因为结果需要从低到顶。所以我下意识先考虑了如何使用递归实现。
然后发现其实使用递归在 Python 中还是很好实现的。
当我在考虑,每一层的节点数量不同,难道还需要构造链表吗?
但是在 Python 中,因为非常动态化的可变参数特性,只需将每一层的所有节点“打包”成元组作为一个参数传下(递归调用)(或者在传递的时候拆包,函数定义上使用 *args)就可以。
想通了这一点,递归的实现方式自然也不难。
这里还是使用队列的按层遍历实现:
class Solution:
def convert_level_order_bottom(self, root):
dq = DQ(root)
ret = []
while not dq.is_empty():
level = []
for _ in range(len(dq)):
node = dq.pop_left()
if node is not None:
level.append(node)
ret.append([_.val for _ in level])
for node in level:
if node.left is not None:
dq.append(node.left)
if node.right is not None:
dq.append(node.right)
return ret[::-1]
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if root is None:
return []
return self.convert_level_order_bottom(root)
199. Binary Tree Right Side View - 获取二叉树的所有最右节点
Solution:
这个问题最一开始还没有想到需要用按层遍历来实现。
主要是这个图不够有代表性,误导很大。
因为这个问题又发掘了 Leetcode 的一个不错的功能,可以可视化二叉树形状:
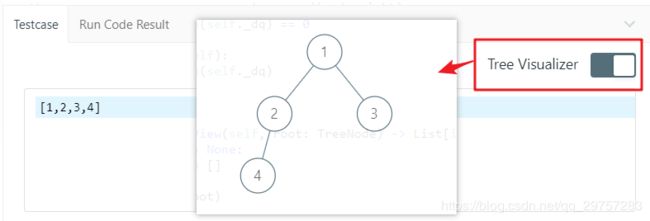
总的来说,最终确认了可以按层遍历算法解决之后,其实代码和上面的几个问题都非常相似。
唯一的区别不过就是将一层中的所有节点读取到一个 level 列表之后用来做什么的区别。
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if root is None:
return []
dq = DQ(root)
ret = []
while not dq.is_empty():
level = list()
for _ in range(len(dq)):
level.append(dq.pop_left())
ret.append(level[-1].val)
for node in level:
if node is not None:
if node.left is not None:
dq.append(node.left)
if node.right is not None:
dq.append(node.right)
else:
raise RuntimeError("Shouldn't run here")
return ret
102. Binary Tree Level Order Traversal - 二叉树按层遍历
Solution:
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if root is None:
return []
ret = []
dq = DQ(root)
node = dq.pop_left()
level_vals = [node.val]
ret.append(level_vals)
dq.append(node.left)
dq.append(node.right)
while not dq.is_empty():
level = list()
for _ in range(len(dq)):
node = dq.pop_left()
if node:
level.append(node)
level_vals = []
for node in level:
if node is not None:
level_vals.append(node.val)
dq.append(node.left)
dq.append(node.right)
if level_vals:
ret.append(level_vals)
return ret
429. N-ary Tree Level Order Traversal - N-ary 树按层遍历
Solution:
仍然使用了队列,代码和 102. Binary Tree Level Order Traversal 几乎完全一样。
只不过对 node.left, node.right 换成了 for child in node.children
"""
# Definition for a Node.
class Node:
def __init__(self, val, children):
self.val = val
self.children = children
"""
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if root is None:
return []
ret = []
dq = DQ(root)
node = dq.pop_left()
level_vals = [node.val]
ret.append(level_vals)
for child in node.children:
dq.append(child)
while not dq.is_empty():
level = list()
for _ in range(len(dq)):
node = dq.pop_left()
if node:
level.append(node)
level_vals = []
for node in level:
if node is not None:
level_vals.append(node.val)
for child in node.children:
dq.append(child)
if level_vals:
ret.append(level_vals)
return ret
559. Maximum Depth of N-ary Tree
Solution:
class Solution:
def get_max_depth(self, root):
dq = DQ(root)
deepth = 0
while not dq.is_empty():
deepth += 1
level = list()
for _ in range(len(dq)):
level.append(dq.pop_left())
for node in level:
if node is not None:
for child in node.children:
dq.append(child)
return deepth
def maxDepth(self, root: 'Node') -> int:
if root is None:
return 0
return self.get_max_depth(root)
637. Average of Levels in Binary Tree - 获取二叉树每一层的平均值
Solution:
和 102. Binary Tree Level Order Traversal 的代码几乎完全一样,只是将 ret.append(level_vals) 简单替换成 ret.append(sum(level_vals)/len(level_vals)) 就可以,其它都不需要改。
虽然执行速度不算快,但是实际上也是稳定的 O ( n ) O(n) O(n) 算法。
构建(整棵)二叉树
108. Convert Sorted Array to Binary Search Tree
Solution:
个人认为针对这个问题而言,使用分治法来构建二叉树是再合适不过的了。
另外再通过递归实现分治法,整个实现其实相当简洁:
class Solution:
def div_constructure_BST(self, nums):
if not len(nums):
return None
if len(nums) == 1:
return TreeNode(nums[0])
half = len(nums) // 2
middle = TreeNode(nums[half])
middle.left = self.div_constructure_BST(nums[:half])
middle.right = self.div_constructure_BST(nums[half + 1:])
return middle
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
return self.div_constructure_BST(nums)
109. Convert Sorted List to Binary Search Tree
Solution:
看到这个问题描述我还纠结了好一会儿如何合理地找到链表的中点。
但是后来转念一想,就算遍历一遍链表,也不过是 O ( n ) O(n) O(n) 的复杂度。
所以遍历一遍链表构建数组,再使用上面 108 实现过的方案,就可以解决这个问题了:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def div_constructure_BST(self, nums):
[...code from 108 ...]
def sortedListToBST(self, head: ListNode) -> TreeNode:
nums = []
curr = head
while curr:
nums.append(curr.val)
curr = curr.next
return self.div_constructure_BST(nums)
公共祖先问题
235. Lowest Common Ancestor of a Binary Search Tree
Solution:
这个问题同样可以使用递归实现。因为二叉搜索树的性质为寻找最低公共祖先简化了算法。
class Solution:
def LCA(self, root, p, q):
lower = min(p.val, q.val)
upper = max(p.val, q.val)
curr = root
if curr.val > upper:
return self.LCA(curr.left, p, q)
elif curr.val < lower:
return self.LCA(curr.right, p, q)
else:
return curr
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
return self.LCA(root, p, q)
110. Balanced Binary Tree - 判断二叉树是否平衡
Solution:
一开始没搞清楚平衡二叉树的定义 - 实现成了判断是否是“完全平衡二叉树”了。
后来重新审视了一下定义。定义已经提供了很强烈的使用递归实现的说法。
所以这里使用递归的实现方法。虽然不会是最快的,但是也不会太慢。因为是 O ( n ) O(n) O(n) 的复杂度,每个节点也就遍历一次。
class Solution:
def get_deepth(self, root):
if root is None:
return 0
if root.left is None and root.right is None:
return 1
left_deepth = 0
right_deepth = 0
if root.left:
left_deepth = self.get_deepth(root.left)
if root.right:
right_deepth = self.get_deepth(root.right)
return max(left_deepth, right_deepth) + 1
def is_balanced(self, root):
if root is None:
return True
if not self.is_balanced(root.left):
return False
if not self.is_balanced(root.right):
return False
left_deepth = self.get_deepth(root.left)
right_deepth = self.get_deepth(root.right)
if abs(left_deepth - right_deepth) <= 1:
return True
else:
return False
def isBalanced(self, root: TreeNode) -> bool:
return self.is_balanced(root)
这个实现唯一要问自己的就是是否有必要加缓存机制(如果对一个子节点不止遍历一次的话),但是最后分析看来是不需要。
112. Path Sum - 判断二叉树是否存在一条根到叶的路径使和为指定值
Solution:
注意满足条件的必须是“根”到“叶”这两个条件!
class Solution:
def has_path_sum(self, root, _sum):
if root is None:
return False
if root.left is None and root.right is None:
if root.val == _sum:
return True
else:
return False
if self.has_path_sum(root.left, (_sum - root.val)):
return True
if self.has_path_sum(root.right, (_sum - root.val)):
return True
return False
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
return self.has_path_sum(root, sum)
226. Invert Binary Tree – 翻转二叉树
Solution:
class Solution:
def invert_tree(self, root):
if root is None:
return None
left = self.invert_tree(root.right)
right = self.invert_tree(root.left)
root.left = left
root.right = right
return root
def invertTree(self, root: TreeNode) -> TreeNode:
return self.invert_tree(root)
404. Sum of Left Leaves
Solution:
def is_leaf(node):
if node is None:
return False
if node.left is None and node.right is None:
return True
return False
class Solution:
def sum_of_left_leaves(self, root):
if root is None:
return 0
if root.left is None:
val1 = 0
elif is_leaf(root.left):
val1 = root.left.val
else:
val1 = self.sum_of_left_leaves(root.left)
if root.right is None:
val2 = 0
else:
val2 = self.sum_of_left_leaves(root.right)
return val1 + val2
def sumOfLeftLeaves(self, root: TreeNode) -> int:
if root is None:
return 0
return self.sum_of_left_leaves(root)
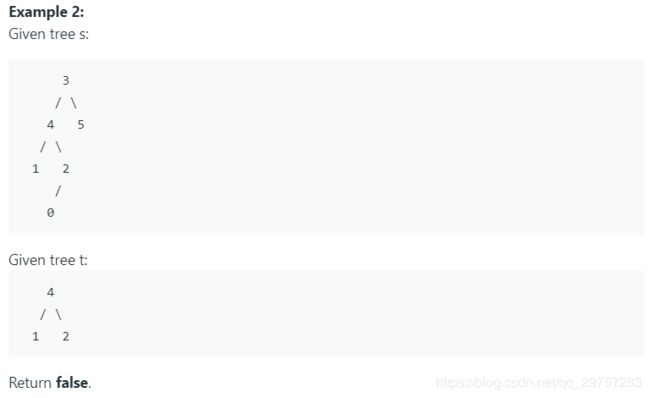
572. Subtree of Another Tree - 判断一棵二叉树是否是另一个二叉树的子树
Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.
Solution:
class Solution:
def level_search(self, level, key):
next_level = []
ret = []
if level:
for node in level:
if node is None:
continue
if node.val == key:
ret.append(node)
next_level.append(node.left)
next_level.append(node.right)
ret.extend(self.level_search(next_level, key))
return ret
def search_nodes(self, root, key):
if root is None:
raise RuntimeError("can't found")
ret = []
if root.val == key:
ret.append(root)
ret.extend(self.level_search([root.left, root.right], key))
if not ret:
raise Exception("can't found")
return ret
def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
try:
sub_roots = self.search_nodes(s, t.val)
except Exception:
return False
else:
return any([self.is_same_tree(_, t) for _ in sub_roots])
其中,.is_same_tree 用到了上文 100. Same Tree 实现过的函数。
在看题目的时候就在想,树中存不存在相同的值。因为这一题没有 Note,然后抱着错了就错了的心态提交了一次,确实是含有相同值的,于是修改代码,实现成将所有值等于 t.val 的子树都找出来判断是否有一个子树完全相同。