scikit-learn Cookbook-1

第一章 模型预处理

1. [从外部源获取样本数据]
   
2. [创建试验样本数据]
   
3. [把数据调整为标准正态分布]
   
4. [用阈值创建二元特征]
   
5. [分类变量处理]
   
6. [标签特征二元化]
   
7. [处理缺失值]
   
8. [用管线命令处理多个步骤]
   
9. [用主成分分析降维]
   
10. [用因子分析降维]
    
11. [用核PCA实现非线性降维]
    
12. [用截断奇异值分解降维]
    
13. [用字典学习分解法分类]
    
14. [用管线命令连接多个转换方法]
    
15. [用正态随机过程处理回归]
    
16. [直接定义一个正态随机过程对象]
    
17. [用随机梯度下降处理回归]
    

1.1 从外部源获取样本数据

默认在sklearn包里面的数据集可以通过datasets.load*?查看。另外一些数据集需要通过datasets.fetch*?下载，这些数据集更大，没有被自动安装。经常用于测试那些解决实际问题的算法。

from sklearn import datasets
import numpy as np

datasets.load_*?

datasets.load_boston
datasets.load_breast_cancer
datasets.load_diabetes
datasets.load_digits
datasets.load_files
datasets.load_iris
datasets.load_linnerud
datasets.load_mlcomp
datasets.load_sample_image
datasets.load_sample_images
datasets.load_svmlight_file
datasets.load_svmlight_files
datasets.load_wine

datasets.fetch_*?

datasets.fetch_20newsgroups
datasets.fetch_20newsgroups_vectorized
datasets.fetch_california_housing
datasets.fetch_covtype
datasets.fetch_kddcup99
datasets.fetch_lfw_pairs
datasets.fetch_lfw_people
datasets.fetch_mldata
datasets.fetch_olivetti_faces
datasets.fetch_openml
datasets.fetch_rcv1
datasets.fetch_species_distributions

# 首先，加载boston数据集看看：
boston = datasets.load_boston()
print(boston.DESCR)

# 下面我们来下载一个数据集：
housing = datasets.fetch_california_housing()
print(housing.DESCR)

X, y = boston.data, boston.target

# 通过datasets.get_data_home()很容易检查默认下载位置。

datasets.get_data_home()

import os 
os.listdir(datasets.get_data_home())

1.2 创建试验样本数据

from sklearn import datasets
datasets.make_*?

datasets.make_biclusters
datasets.make_blobs
datasets.make_checkerboard
datasets.make_circles
datasets.make_classification
datasets.make_friedman1
datasets.make_friedman2
datasets.make_friedman3
datasets.make_gaussian_quantiles
datasets.make_hastie_10_2
datasets.make_low_rank_matrix
datasets.make_moons
datasets.make_multilabel_classification
datasets.make_regression
datasets.make_s_curve
datasets.make_sparse_coded_signal
datasets.make_sparse_spd_matrix
datasets.make_sparse_uncorrelated
datasets.make_spd_matrix
datasets.make_swiss_roll

import sklearn.datasets as d
import numpy as np

reg_data = d.make_regression()
reg_data[0].shape,reg_data[1].shape
# ((100, 100), (100,))

# 创建一个 1000×10的矩阵，5个特征与因变量相关，误差系数0.2，两个因变量。
complex_reg_data = d.make_regression(1000, 10, 5, 2, 1.0)
complex_reg_data[0].shape,complex_reg_data[1].shape
# ((1000, 10), (1000, 2))

classification_set = d.make_classification(weights=[0.1])
np.bincount(classification_set[1])

classification_set[0].shape,classification_set[1].shape
# ((100, 20), (100,))

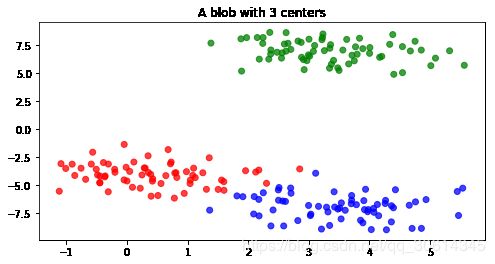
聚类数据集也可以创建。有一些函数可以为不同聚类算法创建对应的数据集。例如，blobs函数可以轻松创建K-Means聚类数据集：

%matplotlib inline
import sklearn.datasets as d
from matplotlib import pyplot as plt
import numpy as np
blobs = d.make_blobs(200)
f = plt.figure(figsize=(8, 4))
ax = f.add_subplot(111)
ax.set_title("A blob with 3 centers")
colors = np.array(['r', 'g', 'b'])
ax.scatter(blobs[0][:, 0], blobs[0][:, 1], color=colors[blobs[1].astype(int)], alpha=0.75)

下面让我们从源代码看看scikit-learn是如何生成回归数据集的。下面任何未重新定义的参数都使用make_regression函数的默认值。其实非常简单。首先，函数调用时生成一个指定维度的随机数组。

n_samples=100;n_features=100;n_target=1;n_informative=10;bias=0.2
# [100,100]
X = np.random.randn(n_samples, n_features)

# [100,1]
ground_truth = np.zeros((n_samples, n_target))
ground_truth[:n_informative, :] = 100*np.random.rand(n_informative,n_target)

# [100,100]*[100,1]=[100,1]
y= np.dot(X, ground_truth) + bias
y.shape
# (100, 1)

1.3 把数据调整为标准正态分布

经常需要将数据标准化调整（scaling）为标准正态分布（standard normal）。标准正态分布算得上是统计学中最重要的分布了。实际上，Z值表的作用就是把服从某种分布的特征转换成标准正态分布的Z值。

from sklearn import preprocessing
import numpy as np

from sklearn import datasets
boston = datasets.load_boston()
X, y = boston.data, boston.target

X[:, :3].mean(axis=0) #前三个特征的均值

X[:, :3].std(axis=0) #前三个特征的标准差

X_2 = preprocessing.scale(X[:, :3])
X_2.mean(axis=0)
X_2.std(axis=0)

中心化与标准化函数很简单，就是减去均值后除以标准差，公式如下所示：
$x=\frac{x-\overline{x}}{\sigma }$

my_scaler = preprocessing.StandardScaler()
my_scaler.fit(X[:, :3])
my_scaler.transform(X[:, :3]).mean(axis=0)

把特征的样本均值变成0，标准差变成1，这种标准化处理并不是唯一的方法。preprocessing还有MinMaxScaler类，将样本数据根据最大值和最小值调整到一个区间内：

my_minmax_scaler = preprocessing.MinMaxScaler()
my_minmax_scaler.fit(X[:, :3])
my_minmax_scaler.transform(X[:, :3]).max(axis=0)

通过MinMaxScaler类可以很容易将默认的区间0到1修改为需要的区间：

my_odd_scaler = preprocessing.MinMaxScaler(feature_range=(-3.14, 3.14))
my_odd_scaler.fit(X[:, :3])
my_odd_scaler.transform(X[:, :3]).max(axis=0)

还有一种方法是正态化（normalization）。它会将每个样本长度标准化为1。这种方法和前面介绍的不同，它的特征值是标量。正态化代码如下：

normalized_X = preprocessing.normalize(X[:, :3])
normalized_X

数据填补（data imputation）是一个内涵丰富的主题，在使用scikit-learn的数据填补功能时需要注意以下两点。

my_useless_scaler = preprocessing.StandardScaler(with_mean=False, with_std=False)
transformed_sd = my_useless_scaler.fit_transform(X[:, :3]).std(axis=0)
original_sd = X[:, :3].std(axis=0)
np.array_equal(transformed_sd, original_sd)
# True

在标准化处理时，稀疏矩阵的处理方式与正常矩阵没太大不同。这是因为数据经过中心化处理后，原来的0值会变成非0值，这样稀疏矩阵经过处理就不再稀疏了：

import scipy
matrix = scipy.sparse.eye(1000)
preprocessing.scale(matrix, with_mean=False)

1.4 用阈值创建二元特征

通常建立二元特征是非常有用的方法，不过要格外小心。我们还是用boston数据集来学习如何创建二元特征。

from sklearn import datasets
boston = datasets.load_boston()
import numpy as np

与标准化处理类似，scikit-learn有两种方法二元特征：

• preprocessing.binarize（一个函数）
• preprocessing.Binarizer（一个类）

target=boston.target.reshape(-1,1)
target.shape

from sklearn import preprocessing
new_target = preprocessing.binarize(target, threshold=target.mean())

bin = preprocessing.Binarizer(target.mean())
new_target = bin.fit_transform(target)
new_target[:5,:]

稀疏矩阵的0是不被存储的；这样可以节省很多空间。这就为binarizer造成了问题，需要指定阈值参数threshold不小于0来解决，如果threshold小于0就会出现错误。

1.5 分类变量处理

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

import numpy as np
d = np.column_stack((X, y))

from sklearn import preprocessing
text_encoder = preprocessing.OneHotEncoder()
text_encoder.fit_transform(d[:, -1:]).toarray()[:5]

text_encoder是一个标准的scikit-learn模型，可以重复使用：

text_encoder.transform(np.ones((3, 1))).toarray()

DictVectorizer

DictVectorizer可以将字符串转换成分类特征：

from sklearn.feature_extraction import DictVectorizer
dv = DictVectorizer()
my_dict = [{'species': iris.target_names[i]} for i in y]
dv.fit_transform(my_dict).toarray()[:5]

1.6 标签特征二元化

from sklearn import datasets as d
iris = d.load_iris()
target = iris.target

from sklearn.preprocessing import LabelBinarizer
label_binarizer = LabelBinarizer()

new_target = label_binarizer.fit_transform(target)

new_target.shape
#(150,3)

new_target[:5]

new_target[-5:]

label_binarizer.classes_

label_binarizer.transform([4])
# array([[0, 0, 0]])

0和1并不一定都是表示因变量中的阳性和阴性实例。例如，如果我们需要用1000表示阳性值，用-1000表示阴性值，我们可以用label_binarizer处理：

label_binarizer = LabelBinarizer(neg_label=-1000, pos_label=1000)
label_binarizer.fit_transform(target)[:5]

1.7 处理缺失值

from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
iris_X = iris.data
masking_array = np.random.binomial(1, .25, iris_X.shape).astype(bool)
iris_X[masking_array] = np.nan

from sklearn import preprocessing
impute = preprocessing.Imputer()
iris_X_prime = impute.fit_transform(iris_X)
iris_X_prime[:5]

上面的计算可以通过不同的方法实现。默认是均值mean，一共是三种：

• 均值mean（默认方法）
• 中位数median
• 众数most_frequent
  scikit-learn会用指定的方法计算数据集中的每个缺失值，然后把它们填充好。
  例如，用median方法重新计算iris_X，重新初始化impute即可：

impute = preprocessing.Imputer(strategy='median')
iris_X_prime = impute.fit_transform(iris_X)
iris_X_prime[:5]

iris_X[np.isnan(iris_X)] = -1
iris_X[:5]

等价于

impute = preprocessing.Imputer(missing_values=-1)
iris_X_prime = impute.fit_transform(iris_X)
iris_X_prime[:5]

pandas库也可以处理缺失值，而且更加灵活，但是重用性较弱：

import pandas as pd
iris_X[masking_array] = np.nan
iris_df = pd.DataFrame(iris_X, columns=iris.feature_names)
iris_df.fillna(iris_df.mean())['sepal length (cm)'].head(5)

iris_df.fillna(iris_df.max())['sepal length (cm)'].head(5)

1.8 用管线命令处理多个步骤

这是我们把多个数据处理步骤组合成一个对象的第一部分。在scikit-learn里称为pipeline。这里我们首先通过计算处理缺失值；然后将数据集调整为均值为0，标准差为1的标准形。

from sklearn import datasets
import numpy as np
mat = datasets.make_spd_matrix(10)

masking_array = np.random.binomial(1, .1, mat.shape).astype(bool)
mat[masking_array] = np.nan
mat[:4, :4]

如果不用管线命令，我们可能会这样实现：

from sklearn import preprocessing
impute = preprocessing.Imputer()
scaler = preprocessing.StandardScaler()
mat_imputed = impute.fit_transform(mat)
mat_imputed[:4, :4]

mat_imp_and_scaled = scaler.fit_transform(mat_imputed)
mat_imp_and_scaled[:4, :4]

现在我们用pipeline来演示：

from sklearn import pipeline
pipe = pipeline.Pipeline([('impute', impute), ('scaler', scaler)])

new_mat = pipe.fit_transform(mat)
new_mat[:4, :4]

np.array_equal(new_mat, mat_imp_and_scaled)
# True

前面曾经提到过，每个scikit-learn的算法接口都类似。pipeline最重要的函数也不外乎下面三个：

• fit
• transform
• fit_transform
  具体来说，如果管线命令有N个对象，前N-1个对象必须实现fit和transform，第N个对象至少实现fit。否则就会出现错误。

1.9 用主成分分析降维

from sklearn import datasets
iris = datasets.load_iris()
iris_X = iris.data

from sklearn import decomposition

pca = decomposition.PCA()
pca

iris_pca = pca.fit_transform(iris_X)
iris_pca[:5]

pca.explained_variance_ratio_
# 在iris数据集中，92.5%的变量可以由第一个主成份表示。

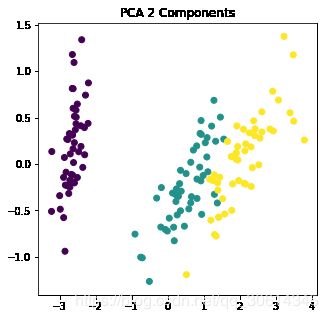
pca = decomposition.PCA(n_components=2)
iris_X_prime = pca.fit_transform(iris_X)
iris_X_prime.shape

%matplotlib inline
from matplotlib import pyplot as plt
f = plt.figure(figsize=(5, 5))
ax = f.add_subplot(111)
ax.scatter(iris_X_prime[:,0], iris_X_prime[:, 1], c=iris.target)
ax.set_title("PCA 2 Components")

pca.explained_variance_ratio_.sum()
# 0.977685206318795

PCA对象还可以一开始设置解释变量的比例。例如，如果我们想介绍98%的变量，PCA对象就可以这样创建：

pca = decomposition.PCA(n_components=.98)
iris_X_prime = pca.fit_transform(iris_X)
pca.explained_variance_ratio_.sum()
# 0.9947878161267247
iris_X_prime.shape
# (150, 3)

1.10 用因子分析降维

因子分析（factor analysis）是另一种降维方法。与PCA不同的是，因子分析有假设而PCA没有假设。因子分析的基本假设是有一些隐藏特征与数据集的特征相关。

让我们再用iris数据集来比较PCA与因子分析，首先加载因子分析类

from sklearn import datasets
iris = datasets.load_iris()
from sklearn.decomposition import FactorAnalysis

fa = FactorAnalysis(n_components=2)
iris_two_dim = fa.fit_transform(iris.data)
iris_two_dim[:5]

%matplotlib inline
from matplotlib import pyplot as plt
f = plt.figure(figsize=(5, 5))
ax = f.add_subplot(111)
ax.scatter(iris_two_dim[:,0], iris_two_dim[:, 1], c=iris.target)
ax.set_title("Factor Analysis 2 Components")

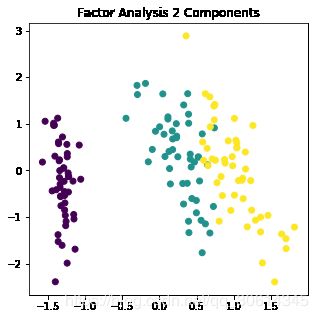
由于因子分析是一种概率性的转换方法，我们可以通过不同的角度来观察，例如模型观测值的对数似然估计值，通过模型比较对数似然估计值会更好。

因子分析也有不足之处。由于你不是通过拟合模型直接预测结果，拟合模型只是一个中间步骤。这本身并非坏事，但是训练实际模型时误差就会产生。

因子分析与前面介绍的PCA类似。但两者有一个不同之处。PCA是通过对数据进行线性变换获取一个能够解释数据变量的主成分向量空间，这个空间中的每个主成分向量都是正交的。你可以把PCA看成是$N$维数据集降维成$M$维，其中$M<N$。

而因子分析的基本假设是，有$M$个重要特征和它们的线性组合（加噪声），能够构成原始的$N$维数据集。也就是说，你不需要指定结果变量（就是最终生成$N$维），而是要指定数据模型的因子数量（$M$个因子）。

1.11 用核PCA实现非线性降维

核主成分分析（Kernel PCA）可以处理非线性问题。数据先通过核函数（kernel function）转换成一个新空间，然后再用PCA处理。

要理解核函数之前，建议先尝试如何生成一个能够通过核PCA里的核函数线性分割的数据集。下面我们用余弦核（cosine kernel）演示。

余弦核可以用来比例样本空间中两个样本向量的夹角。当向量的大小（magnitude）用传统的距离度量不合适的时候，余弦核就有用了。

向量夹角的余弦公式如下：$\cos (\theta )=\frac{A\cdot B}{\Vert A\Vert \Vert B\Vert }$

向量AA和BB夹角的余弦是两向量点积除以两个向量各自的L2范数。向量AA和BB的大小不会影响余弦值。

import numpy as np

A1_mean = [1, 1]
A1_cov = [[2, .99], [1, 1]]
# 生成一个多元正态分布矩
A1 = np.random.multivariate_normal(A1_mean, A1_cov, 50)

A2_mean = [5, 5]
A2_cov = [[2, .99], [1, 1]]
A2 = np.random.multivariate_normal(A2_mean, A2_cov, 50)

A = np.vstack((A1, A2))
B_mean = [5, 0]
B_cov = [[.5, -1], [.9, -.5]]
B = np.random.multivariate_normal(B_mean, B_cov, 100)

import matplotlib.pyplot as plt
%matplotlib inline
f = plt.figure(figsize=(10, 10))
ax = f.add_subplot(111)
ax.set_title("$A$ and $B$ processes")
ax.scatter(A[:, 0], A[:, 1], color='r')
ax.scatter(A2[:, 0], A2[:, 1], color='r')
ax.scatter(B[:, 0], B[:, 1], color='b')

上图看起来明显是两个不同的过程数据，但是用一超平面分割它们很难。因此，我们用前面介绍带余弦核的核PCA来处理：

from sklearn.decomposition import KernelPCA
kpca = KernelPCA(kernel='cosine', n_components=1)
AB = np.vstack((A, B))
AB_transformed = kpca.fit_transform(AB)

A_color = np.array(['r']*len(B))
B_color = np.array(['b']*len(B))
colors = np.hstack((A_color, B_color))
f = plt.figure(figsize=(10, 4))
ax = f.add_subplot(111)
ax.set_title("Cosine KPCA 1 Dimension")
ax.scatter(AB_transformed, np.zeros_like(AB_transformed), color=colors)

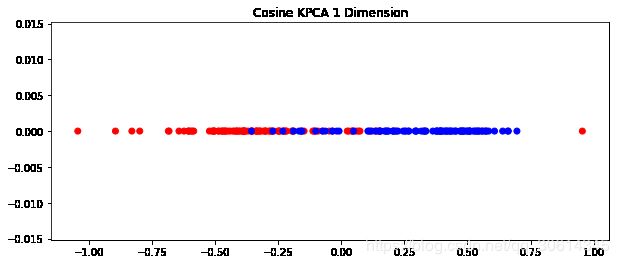
用带余弦核的核PCA处理后，数据集变成了一维。如果用PCA处理就是这样：

from sklearn.decomposition import PCA
pca = PCA(1)
AB_transformed_Reg = pca.fit_transform(AB)
f = plt.figure(figsize=(10, 4))
ax = f.add_subplot(111)
ax.set_title("PCA 1 Dimension")
ax.scatter(AB_transformed_Reg, np.zeros_like(AB_transformed_Reg), color=colors)

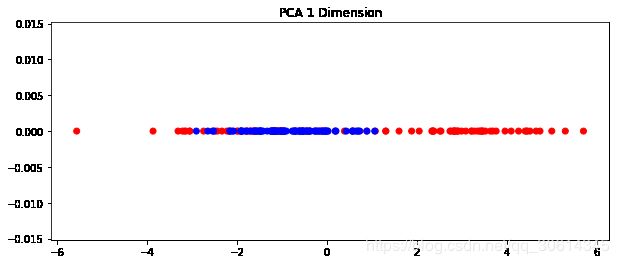
scikit-learn提供了几种像余弦核那样的核函数，也可以写自己的核函数。默认的函数有：

• 线性函数（linear）（默认值）
• 多项式函数（poly）
• 径向基函数（rbf，radial basis function）
• S形函数（sigmoid）
• 余弦函数（cosine）
• 用户自定义函数（precomputed）
  还有一些因素会影响核函数的选择。例如，degree参数可以设置poly，rbf和sigmoid核函数的角度；而gamma会影响rbf和poly核，更多详情请查看KernelPCA文档。

1.12 用截断奇异值分解降维

截断奇异值分解（Truncated singular value decomposition，TSVD）是一种矩阵因式分解（factorization）技术，将矩阵$M$分解成$U$，$\Sigma$和$V$。它与PCA很像，只是SVD分解是在数据矩阵上进行，而PCA是在数据的协方差矩阵上进行。通常，SVD用于发现矩阵的主成份。

TSVD与一般SVD不同的是它可以产生一个指定维度的分解矩阵。例如，有一个$n\times n$矩阵，通过SVD分解后仍然是一个$n\times n$矩阵，而TSVD可以生成指定维度的矩阵。这样就可以实现降维了。

from sklearn.datasets import load_iris
iris = load_iris()
iris_data = iris.data

from sklearn.decomposition import TruncatedSVD

svd = TruncatedSVD(2)
iris_transformed = svd.fit_transform(iris_data)
iris_data[:5]

iris_transformed.shape
# (150)

%matplotlib inline
import matplotlib.pyplot as plt
f = plt.figure(figsize=(5, 5))
ax = f.add_subplot(111)
ax.scatter(iris_transformed[:, 0], iris_transformed[:, 1], c=iris.target)
ax.set_title("Truncated SVD, 2 Components")

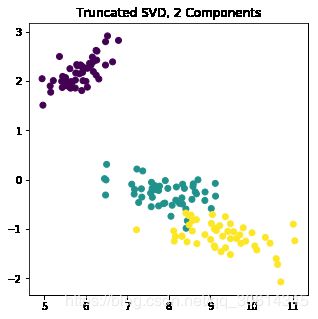
现在我们演示了scikit-learn的TruncatedSVD模块，让我们看看只用scipy学习一些细节。

import numpy as np
from scipy.linalg import svd
D = np.array([[1, 2], [1, 3], [1, 4]])
D

U, S, V = svd(D, full_matrices=False)
U.shape, S.shape, V.shape
# ((3, 2), (2,), (2, 2))
np.diag(S)

np.dot(U.dot(np.diag(S)), V)

new_S = S[0]
new_U = U[:, 0]
new_U.dot(new_S)

1.13 用字典学习分解法分类

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import load_iris
iris = load_iris()
iris_data = iris.data
iris_target = iris.target

from sklearn.decomposition import DictionaryLearning
dl = DictionaryLearning(3)

transformed = dl.fit_transform(iris_data[::2])
transformed[:5]

from mpl_toolkits.mplot3d import Axes3D
colors = np.array(list('rgb'))
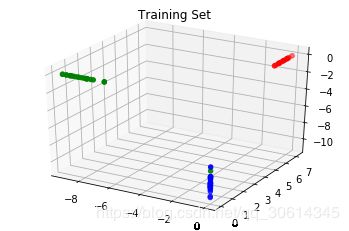
f = plt.figure()
ax = f.add_subplot(111, projection='3d')
ax.set_title("Training Set")
ax.scatter(transformed[:, 0], transformed[:, 1], transformed[:, 2], 
color=colors[iris.target[::2]]);

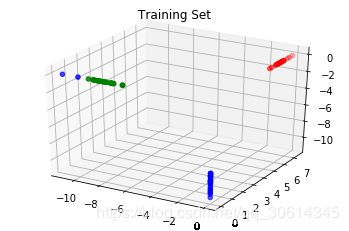
transformed = dl.transform(iris_data[1::2])

colors = np.array(list('rgb'))
f = plt.figure()
ax = f.add_subplot(111, projection='3d')
ax.set_title("Training Set")
ax.scatter(transformed[:, 0], transformed[:, 1], transformed[:, 2], 
color=colors[iris.target[1::2]]);

1.14 用管线命令连接多个转换方法

from sklearn.datasets import load_iris
import numpy as np
iris = load_iris()
iris_data = iris.data
mask = np.random.binomial(1, .25, iris_data.shape).astype(bool)
iris_data[mask] = np.nan
iris_data[:5]

from sklearn import pipeline, preprocessing, decomposition

pca = decomposition.PCA()
imputer = preprocessing.Imputer()

pipe = pipeline.Pipeline([('imputer', imputer), ('pca', pca)])
np.set_printoptions(2)
iris_data_transformed = pipe.fit_transform(iris_data)
iris_data_transformed[:5]

管线命令的每个步骤都是用一个元组表示，元组的第一个元素是对象的名称，第二个元素是对象。

本质上，这些步骤都是在管线命令调用时依次执行fit_transform方法。还有一种快速但不太简洁的管线命令建立方法，就像我们快速建立标准化调整模型一样，只不过用StandardScaler会获得更多功能。pipeline函数将自动创建管线命令的名称：

pipe2 = pipeline.make_pipeline(imputer, pca)
pipe2.steps

iris_data_transformed2 = pipe2.fit_transform(iris_data)
iris_data_transformed2[:5]

管线命令连接内部每个对象的属性是通过set_params方法实现，其参数用<对象名称>__<对象参数>表示。例如，我们设置PCA的主成份数量为2：

pipe2.set_params(pca__n_components=2)

iris_data_transformed3 = pipe2.fit_transform(iris_data)
iris_data_transformed3[:5]

1.15 用正态随机过程处理回归

这个主题将介绍如何用正态随机过程（Gaussian process，GP）处理回归问题。在线性模型部分，我们曾经见过在变量间可能存在相关性时，如何用贝叶斯岭回归(Bayesian Ridge Regression)表示先验概率分布（prior）信息。

正态分布过程关心的是方差而不是均值。但是，如果我们假设一个正态分布的均值为0，那么我们需要确定协方差。

这样处理就与线性回归问题中先验概率分布可以用相关系数表示的情况类似。用GP处理的先验就可以用数据、样本数据间协方差构成函数表示，因此必须从数据中拟合得出。

import numpy as np
from sklearn.datasets import load_boston
boston = load_boston()
boston_X = boston.data
boston_y = boston.target
train_set = np.random.choice([True, False], len(boston_y), p=[.75, .25])

有了数据之后，我们就创建scikit-learn的GaussianProcess对象。默认情况下，它使用一个常系数回归方程（constant regression function）和平方指数相关函数（ squared exponential correlation），是最主流的选择之一：

from sklearn.gaussian_process import GaussianProcessRegressor
gp = GaussianProcessRegressor()
gp.fit(boston_X[train_set], boston_y[train_set])

test_preds = gp.predict(boston_X[~train_set])

让我们把预测值和实际值画出来比较一下。因为我们做了回归，还可以看看残差散点图和残差直方图。

%matplotlib inline
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(10, 7), nrows=3)
f.tight_layout()
ax[0].plot(range(len(test_preds)), test_preds, label='Predicted Values');
ax[0].plot(range(len(test_preds)), boston_y[~train_set], label='Actual Values');
ax[0].set_title("Predicted vs Actuals")
ax[0].legend(loc='best')
ax[1].plot(range(len(test_preds)),test_preds - boston_y[~train_set]);
ax[1].set_title("Plotted Residuals")
ax[2].hist(test_preds - boston_y[~train_set]);
ax[2].set_title("Histogram of Residuals");

from sklearn.gaussian_process.kernels import RBF
kernel = 1 * RBF(length_scale = 1)
gp = GaussianProcessRegressor(kernel=kernel, alpha=5e-1)

gp.fit(boston_X[train_set], boston_y[train_set])
linear_preds = gp.predict(boston_X[~train_set])

f, ax = plt.subplots(figsize=(7, 5))
f.tight_layout()
ax.hist(test_preds - boston_y[~train_set],label='Residuals Original', color='b', alpha=.5);
ax.hist(linear_preds - boston_y[~train_set],label='Residuals Linear', color='r', alpha=.5);
ax.set_title("Residuals")
ax.legend(loc='best');

np.power(test_preds - boston_y[~train_set], 2).mean()

np.power(linear_preds - boston_y[~train_set], 2).mean()

https://yhs-968.github.io/ml/2017/02/13/Gaussian-Process-Regression-with-scikit-learn-for-the-GPML.html

1.16 直接定义一个正态随机过程对象

gaussian_process模块可以直接连接不同的相关函数与回归方程。这样就可以不创建GaussianProcess对象，直接通过函数创建需要的对象。

from sklearn.datasets import make_regression
X, y = make_regression(1000, 1, 1)
from sklearn.gaussian_process import regression_models

# 第一个相关函数是常系数相关函数。它有若干常数构成：
regression_models.constant(X)[:5]

# 还有线性相关函数与平方指数相关函数，它们也是GaussianProcess类的默认值：
regression_models.linear(X)[:1]

regression_models.quadratic(X)[:1]

1.17 用随机梯度下降处理回归

from sklearn import datasets
X, y = datasets.make_regression(int(1e6))
print("{:,}".format(int(1e6)))

print("{:,}".format(X.nbytes))

X.nbytes / 1e6

X.nbytes / (X.shape[0] * X.shape[1])

import numpy as np
from sklearn import linear_model
sgd = linear_model.SGDRegressor()
train = np.random.choice([True, False], size=len(y), p=[.75, .25])
sgd.fit(X[train], y[train])

linear_preds = sgd.predict(X[~train])

%matplotlib inline
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(7, 5))
f.tight_layout()
ax.hist(linear_preds - y[~train],label='Residuals Linear', color='b', alpha=.5);
ax.set_title("Residuals")
ax.legend(loc='best');