数据结构之树和堆
最优二叉树
哈夫曼树是带权路径最小的一种特殊二叉树,所以也称最优二叉树。
在这里不讨论基本概念如如何计算路径等,而只着重于树的创建,具体过程让我们举例而言。
其基本的原理为:将所有节点一开始都视为森林,每次从森林中选取两个根节点权值最小的树合并为一棵新树,新树的根节点大小为两个子节点大小的和,并将这棵新树重新加入到森林中。
如此一来每一轮操作都可以简化为两个基本操作:合并两棵树、插入新树,直到森林中只剩下一棵树,即是哈夫曼树。
from:https://blog.csdn.net/hd12370/article/details/82877211
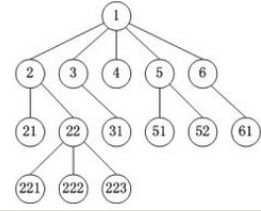
有序树
每棵树的子树都按照从左到右的顺序依次排列,不会出现没有左侧的子树而有右侧子树的情况。
树中任意节点的子结点之间有顺序关系,这种树称为有序树。
堂兄弟:即同一父亲下的所有子树
如何将有序树转换为二叉树
则有序树的结点的后序遍历是二叉树结点的中序遍历。
1. 二叉树
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有![]() 个结点;深度为k的二叉树至多有
个结点;深度为k的二叉树至多有![]() 个结点。
个结点。
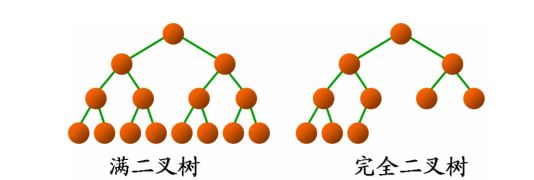
满二叉树和完全二叉树:
满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点。一颗树深度为h,最大层数为k,深度与最大层数相同,总节点数一定是奇数。
完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。
注:完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
2. 二叉查找树排序树
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2) 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
3) 没有键值相等的节点。
二叉查找树的性质:对二叉查找树进行中序遍历,即可得到有序的数列。二叉查找树的高度决定了二叉查找树的查找效率。
二叉查找树的插入过程如下:
1) 若当前的二叉查找树为空,则插入的元素为根节点;
2) 若插入的元素值小于根节点值,则将元素插入到左子树中;
3) 若插入的元素值不小于根节点值,则将元素插入到右子树中。
二叉查找树的删除,分三种情况进行处理:
1) p为叶子节点,直接删除该节点,再修改其父节点的指针(注意分是根节点和不是根节点),如图a;
2) p为单支节点(即只有左子树或右子树)。让p的子树与p的父亲节点相连,删除p即可(注意分是根节点和不是根节点),如图b;
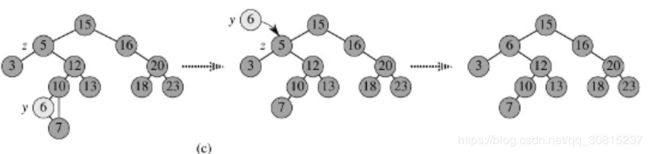
3) p的左子树和右子树均不空。找到p的后继y(右子树内的最小节点),y一定没有左子树,所以可以删除y,并让y的父亲节点成为y的右子树的父亲节点,并用y的值代替p的值;
或者方法二是找到p的前驱x(左子树内的最大节点),x一定没有右子树,所以可以删除x,并让x的父亲节点成为x的左子树的父亲节点。如图c。
from :https://www.cnblogs.com/maybe2030/p/4732377.html#_label1
二叉树的遍历
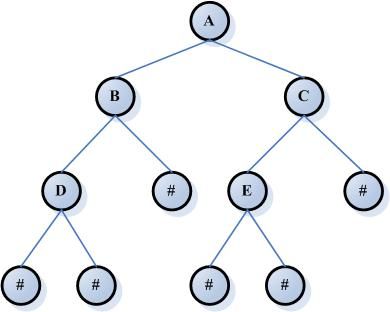
二叉树中最重要的操作就是遍历,通常有中序遍历,前序遍历和后序遍历,中序遍历就是左,根,右;而前序遍历是根,左,右;后序遍历则是左,右,根。
例如 A:根节点、B:左节点、E:右节点,前序顺序是ABE(根节点排最先,然后同级先左后右);中序顺序是BAE(先左后根最后右);后序顺序是BEA(先左后右最后根)。
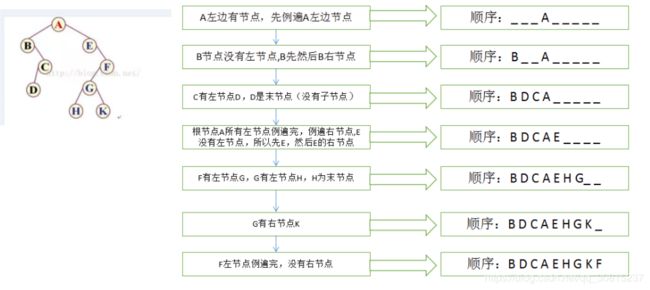
分析中序遍历如下图:
前序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
后序遍历:DCBHKGFEA
已知2个,可以求另一个:首先前序中,第一个是根节点,第二个是根的左节点;后序中,最后一个是根节点;中序中,根节点后面紧跟着的是根节点的右节点。
from:https://blog.csdn.net/qq_33243189/article/details/80222629
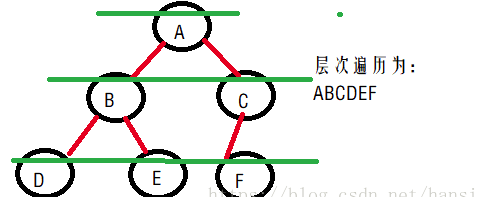
层次遍历:
二叉树的层次遍历借助一个队列来实现:
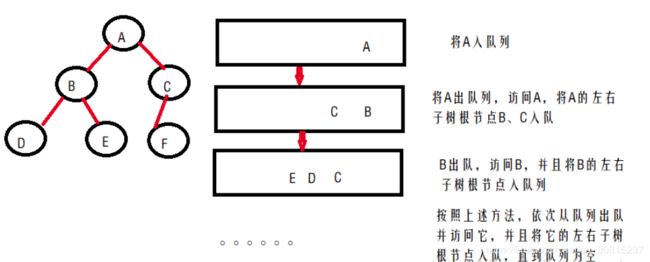
先将二叉树根节点入队,然后出队,访问该节点,如果有左子树,则将左子树根节点入队;如果有右子树,则将右子树根节点入队。然后出队,对出队节点访问,如此循环,直到队列为空。如下图所示:注意图中右侧表示队尾,左侧表示队头。
from:https://blog.csdn.net/hansionz/article/details/81947834
3、平衡二叉树
我们知道,对于一般的二叉搜索树(Binary Search Tree),其期望高度(即为一棵平衡树时)为log2n,其各操作的时间复杂度O(log2n)同时也由此而决定。但是,在某些极端的情况下(如在插入的序列是有序的时),二叉搜索树将退化成近似链或链,此时,其操作的时间复杂度将退化成线性的,即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。于是就有了我们下边介绍的平衡二叉树。
平衡二叉树定义:平衡二叉树(Balanced Binary Tree)具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用算法有红黑树、AVL树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log2n),大大降低了操作的时间复杂度。
最小二叉平衡树的节点的公式:F(n)=F(n-1)+F(n-2)+1
这个类似于一个递归的数列,可以参考Fibonacci数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。
3.1、AVL树
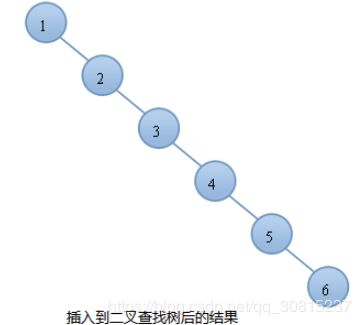
AVL树定义:AVL树是最先发明的自平衡二叉查找树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,在AVL中任何节点的两个儿子子树的高度最大差别为1,所以它也被称为高度平衡树,n个结点的AVL树最大深度约1.44log2n。查找、插入和删除在平均和最坏情况下都是O(logn)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。例如:我们按顺序将一组数据1,2,3,4,5,6分别插入到一颗空二叉查找树和AVL树中,插入的结果如下图:
由上图可知,同样的结点,由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下,会导致二叉树的高度是O(N),而AVL树就不会出现这种情况,树的高度始终是O(lgN).高度越小,对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因。
这里我们关注的是两个变化很大的操作:插入和删除!
我们知道,AVL树不仅是一颗二叉查找树,它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理,在删除的时候也有可能会破坏树的平衡性,所以我们要做一些特殊的处理,包括:单旋转和双旋转!
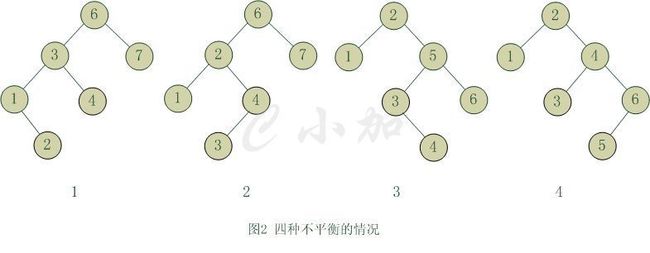
旋转主要是为了实现AVL树在实施了插入和删除操作以后,树重新回到平衡的方法。对于一个平衡的节点,由于任意节点最多有两个儿子,因此高度不平衡时,此节点的两颗子树的高度差2.容易看出,这种不平衡出现在下面四种情况:
1) 6节点的左子树3节点高度比右子树7节点大2,左子树3节点的左子树1节点高度大于右子树4节点,这种情况成为左左。
2) 6节点的左子树2节点高度比右子树7节点大2,左子树2节点的左子树1节点高度小于右子树4节点,这种情况成为左右。
3) 2节点的左子树1节点高度比右子树5节点小2,右子树5节点的左子树3节点高度大于右子树6节点,这种情况成为右左。
4) 2节点的左子树1节点高度比右子树4节点小2,右子树4节点的左子树3节点高度小于右子树6节点,这种情况成为右右。
从图2中可以可以看出,1和4两种情况是对称的,这两种情况的旋转算法是一致的,只需要经过一次旋转就可以达到目标,我们称之为单旋转。2和3两种情况也是对称的,这两种情况的旋转算法也是一致的,需要进行两次旋转,我们称之为双旋转。
单旋转
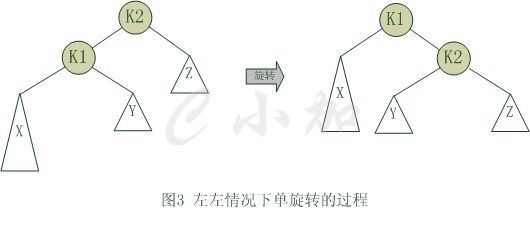
单旋转是针对于左左和右右这两种情况的解决方案,这两种情况是对称的,只要解决了左左这种情况,右右就很好办了。图3是左左情况的解决方案,节点k2不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的左子树X子树,所以属于左左情况。
为使树恢复平衡,我们把k2变成这棵树的根节点,因为k2大于k1,把k2置于k1的右子树上,而原本在k1右子树的Y大于k1,小于k2,就把Y置于k2的左子树上,这样既满足了二叉查找树的性质,又满足了平衡二叉树的性质。
这样的操作只需要一部分指针改变,结果我们得到另外一颗二叉查找树,它是一棵AVL树,因为X向上一移动了一层,Y还停留在原来的层面上,Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同,插入操作使得X高度长高了。因此,由于这颗子树高度没有变化,所以通往根节点的路径就不需要继续旋转了。
双旋转
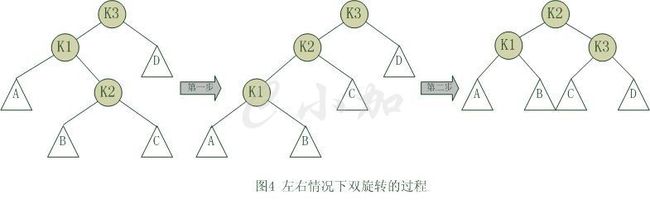
对于左右和右左这两种情况,单旋转不能使它达到一个平衡状态,要经过两次旋转。双旋转是针对于这两种情况的解决方案,同样的,这样两种情况也是对称的,只要解决了左右这种情况,右左就很好办了。图4是左右情况的解决方案,节点k3不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的右子树k2子树,所以属于左右情况。
为使树恢复平衡,我们需要进行两步,第一步,把k1作为根,进行一次右右旋转,旋转之后就变成了左左情况,所以第二步再进行一次左左旋转,最后得到了一棵以k2为根的平衡二叉树。
from:https://www.cnblogs.com/maybe2030/p/4732377.html
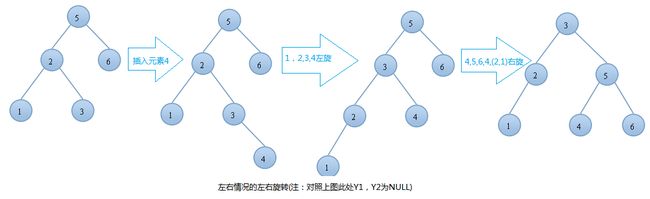
左右情况的左右旋转实例:
4、堆
堆就是用数组实现的二叉树,所有它没有使用父指针或者子指针。堆根据“堆属性”来排序,“堆属性”决定了树中节点的位置。它是利用完全二叉树的结构来维护一组数据,然后进行相关操作,一般的操作进行一次的时间复杂度在O(1)~O(logn)之间。
在最大堆中,父节点的值比每一个子节点的值都要大。在最小堆中,父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”,并且这个属性对堆中的每一个节点都成立。(注意堆:对左右子节点没有大小要求)
堆的常用方法:
- 构建优先队列
- 支持堆排序
- 快速找出一个集合中的最小值(或者最大值)
堆还分为两种类型:大根堆、小根堆,就是保证根节点是所有数据中最大/小,并且尽力让小的节点在上方
不过有一点需要注意:错误的认为大/小根堆中下标为1就是第一大/小,2是第二大/小……
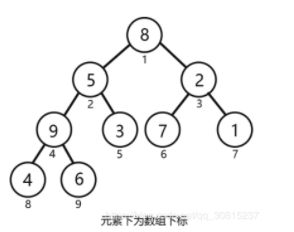
让我们加入一组数据吧!下标从1到9分别加入:{8,5,2,9,3,7,1,4,6}。如下图所示
堆的几个基本操作:
- 上浮 shift_up;
- 下沉 shift_down
- 插入 push
- 弹出 pop
- 取顶 top
我们以小根堆为例
我们很容易就能看出,根节点1元素8不是最小的,它的子节点3(元素2)比它来的小,我们怎么将它放到最高点呢?很简单,直接交换,又发现节点3的子节点7(元素1)似乎更适合在根节点。这时候我们是无法直接和根节点交换的,那我们就需要一个操作来实现这个交换过程,那就是上浮 shift_up。
操作过程如下:
从当前结点开始,和它的父节点比较,若是比父节点来的小,就交换,然后将当前询问的节点下标更新为原父节点下标;否则退出。操作图示:
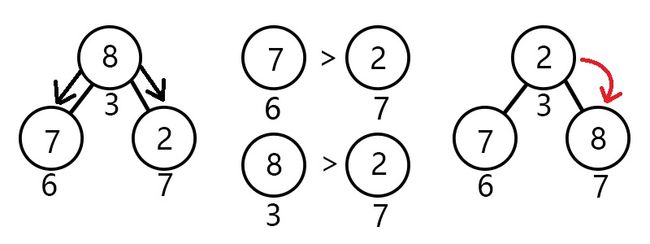
一次上浮完毕之后,发现节点3(元素8)不太合适放在那,那么问题来了:节点3应该往哪下沉呢?我们知道,小根堆是尽力要让小的元素在较上方的节点,而下沉与上浮一样要以交换来不断操作,所以我们应该让节点7与其交换。
由此我们可以得出下沉的算法了:
让当前结点的子节点(如果有的话)作比较,哪个比较小就和它交换,并更新询问节点的下标为被交换的儿子节点下标,否则退出。模拟操作图示:
接下来是插入操作
我们前面用的插入是直接插入,所以数据才会杂乱无章,那么我们如何在插入的时候边维护堆呢?其实很简单,每次插入的时候呢,我们都往最后一个插入,让后使它上浮。
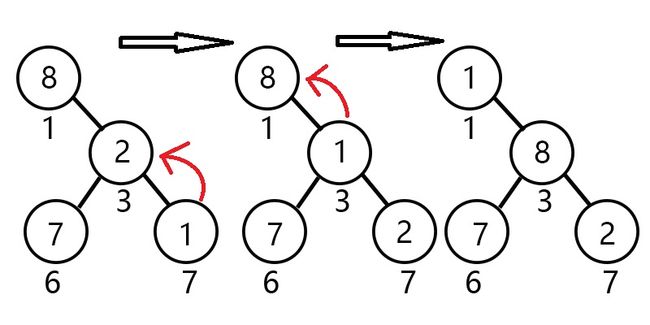
弹出:
顾名思义就是把顶元素弹掉,但是,弹掉以后不是群龙无首吗??我们如何去维护这堆数据呢?我们得出一个十分巧妙的算法:让根节点元素和尾节点进行交换,然后让现在的根元素下沉就可以了!
取顶:
根节点数组下标必定是1,返回堆[ 1 ]就OK注意:每次取顶要判断堆内是否有元素,
from:https://www.cnblogs.com/JVxie/p/4859889.html
堆可用于排序:
动图演示:
from:https://www.runoob.com/w3cnote/heap-sort.html