《统计学习方法》—— k近邻方法、kd树以及python3实现

前言

k近邻方法的初衷很简单，就是找最近的k个数据，根据这些数据的标记，按照某种规则，给新的数据标记。这里，我们可以看到三个重点：k值，距离度量和决策规则。

• k值决定方法的复杂程度。考虑k很大，足以包括所有数据的时候，此时给新的数据标记结果，必然由大多数相同标记决定，而少部分数据的信息则被忽略，这时，方法是欠拟合的，简单的；而当k=1时，此时新数据标记则直接根据最近的数据标记，对于众多的新数据，原有数据集的信息是被充分利用的，但是会过拟合，方法是复杂的。
• 度量距离决定如何找到k个数据。在不同的距离度量下，找到的最近数据可能不一样。可以这样构造例子，有三个数据$x_1$，$x_2$和$x_3$。我们令$x_1$和$x_2$只有一维不同，其余维度上数值都相同，而$x_1$和$x_3$在多个维度上数值不同。这样，在$L_p$范数下，距离${\Vert x_1-x_2\Vert }_p$保持不变；而${\Vert x_1-x_3\Vert }_p$则随着p的增加而增加。显然，在p较小时，${\Vert x_1-x_2\Vert }_p>{\Vert x_1-x_3\Vert }_p$；而p较大时，${\Vert x_1-x_2\Vert }_p<{\Vert x_1-x_3\Vert }_p$。这就说明不同度量距离下，某个数据的最近点可能会发生改变。（具体可见李航《统计学习方法》第二版 例3.1）
• 决策规则决定如何给新数据标记。一般我们常用多数表决规则，也就是说，我们将k个数据中占多数的标记，作为新数据的标记。

注意：本文参考了大佬@火烫火烫的的代码。

1. k近邻算法

直接给算法。

• 输入：数据集 $T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中，$x_i\in {\mathbb{R}}^n$，$y_i\in \{c_1,c_2,...,c_k\}$；新数据 $x_{N+1}$
• 输出：新数据 $x_{N+1}$ 的标记 $y_{N+1}$

记 $N_k(x)$ 为$x$的k邻域，即 $N_k(x)$是距离$x$最近的k个数据的集合。这样，当决策规则是多数表决的时候，标记$y_{N+1}$由下式给出 $$y_{N+1}=\underset{c\in \{c_1,c_2,...,c_k\}}{\mathrm{argmax}}\sum _{x_i\in N_k(x_{N+1})}I(y_i=c)$$

其中，$I(\cdot )$为指示函数。

实际上，上式说明多数表决规则实际上是经验损失最小化的。这里的损失函数$L$取0-1损失函数。我们有
$$\begin{array}{lll}{y}_{N+1}& =& \underset{c\in \{c_1,c_2,...,c_k\}}{\mathrm{argmax}}{\sum }_{x_i\in N_k(x_{N+1})}I(y_i=c)\\ & =& \underset{c\in \{c_1,c_2,...,c_k\}}{\mathrm{argmax}}\frac{1}{k}\cdot {\sum }_{x_i\in N_k(x_{N+1})}I(y_i=c)\\ & =& \underset{c\in \{c_1,c_2,...,c_k\}}{\mathrm{argmin}}\frac{1}{k}\cdot {\sum }_{x_i\in N_k(x_{N+1})}I(y_i\ne c)\\ & =& \underset{c\in \{c_1,c_2,...,c_k\}}{\mathrm{argmin}}\frac{1}{k}\cdot {\sum }_{x_i\in N_k(x_{N+1})}L(y_i,c)\end{array}$$

2. kd树

从k近邻算法，我们有一个直观的代码实现，也就是 遍历数据集 $T$，计算每个数据与新数据的距离，选取其中最小的k个数据，作为k近邻。

但上述算法面对海量数据的时候，需要将海量数据逐个计算一遍距离，较为消耗时间。我们可以用一种名为 kd树 的数据结构来帮助我们节省时间。

下面，我们将针对 最近邻问题(即，k=1的情形) 来进行讨论。

2.1 一维数组的查找

我们首先考虑给定一个数$x$，如何在一维数组$[x_1,x_2,...,x_N]$中找出这个数的最近邻问题。

比如，在数组 $[3,6,2,9,10,7,4]$ 中，找到5的最近邻。

除了线性扫描这个$O(N)$的做法之外，我们寻求更快的做法。实际上，通过构建kd树以及在kd树上查找，我们可以将问题的时间复杂度降为 $O(lgN)$。

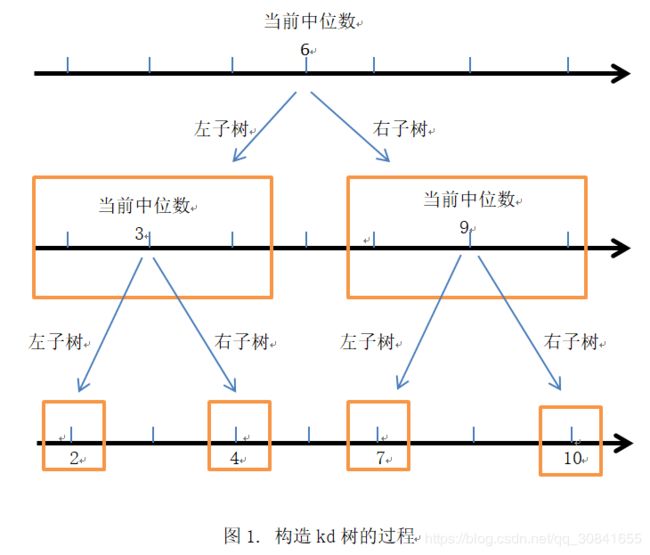
构建 kd树：
(1) 找到当前数组的中位数，并将中位数移到数组中间位置
(2) 将中位数作为结点，其左结点由中位数左边数组构建，其右结点由中位数右边数组构建；构建时回到步骤 (1)

该过程显然用递归。

• 找出数组中位数，并将中位数放在数组中间

# 找出中位数，并将中位数放在中间位置
## 借助快速排序的partition函数
def partition(left, right): # 数组nums[left:right+1]
	if left >= right:
		return 
	pivot = nums[left]
	i, j = left, right
	while i < j:
		while i < j and nums[j] >= pivot:
			j -= 1
		nums[i] = nums[j]
		while i < j and nums[i] < pivot:
			i += 1
		nums[j] = nums[i]
	nums[i] = pivot
	return i
	
def getMedium(left, right, k): # nums[left: right+1]的第k小的数
	if left >= right:
		return nums[left]
	
	index = merging(left, right)
	if index == k:
		return nums[k]
	elif index < k:
		left = index + 1
	else:
		right = index
	return getMedium(left, right, k)

上述程序能够返回中位数并将中位数放在数组中间位置

nums = [3, 6, 2, 9, 10, 7, 4]
print('原始数组nums=', nums)
print('原始数组的中位数为', getMedium(0, len(nums)-1))
print('调整过的数组nums=', nums)

原始数组nums= [3, 6, 2, 9, 10, 7, 4]
原始数组的中位数为 6
调整过的数组nums= [2, 3, 4, 6, 10, 7, 9]

上面找中位数的算法平均时间复杂度为$O(N)$，比冒泡排序（$O(N^2)$）要好。

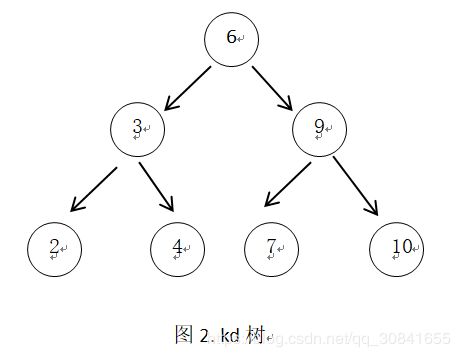
• 构造kd树

# 定义结点
class Node:
	def __init__(self, data, left=None, right=None):
		self.data = data
		self.left = left
		self.right = right

# 递归构造kd树
def kdTree(i, j): # 通过数组nums[i:j+1]构建kd树
    if i == j:
        return Node(nums[i])
    if i > j:
        return None
    
    mid = (j+i+1)//2 # 中位数位置
    
    root = Node(getMedium(i, j, mid))
    #print('left=', [i, mid-1])
    #print('right=', [mid+1, j])
    
    root.left = kdTree(i, mid-1)
    root.right = kdTree(mid+1, j)
    
    return root

我们用中序遍历来看一下结果

# 中序遍历，返回数组
def inorder(root):
	return inorder(root.left) + [root.data] + inorder(root.right) if root else []

# 初始数组
nums = [3, 6, 2, 9, 10, 7, 4]
# 构建kd树
print('构建的kd树的中序遍历为')
print(inorder(root))

构建的kd树的中序遍历为
[2, 3, 4, 6, 7, 9, 10]

观察结果，可以看到是正确的。

构造kd树的过程，如图1：

构造后的kd树，如图2：

• kd树查找

我们想找5的最近邻：
（1）递归向下，直到叶子结点，如图3所示

（2）沿着原来的路径返回，在每个节点更新最近邻距离，并判断是否需要进入当前节点的另一边子树

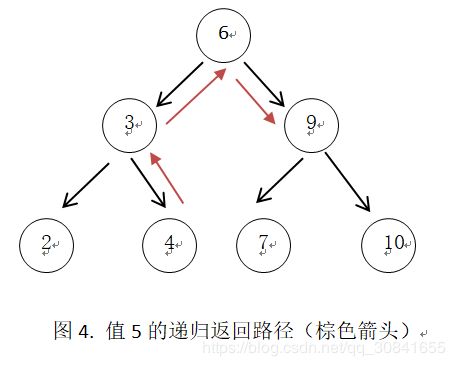
进一步的，我们可以将值5的具体过程作在图5中，

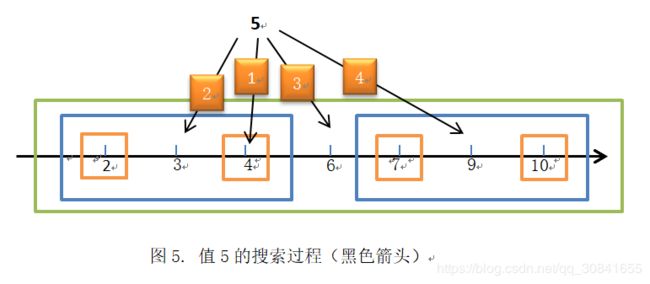
在图5中，我们可以看到，

• 5首先在叶节点4所在的黄色方框里面，得到最近邻距离1
• 然后退回路径，进入父节点3所在的蓝色方框里面，由于5和3之间差距为2，大于最近邻距离1，所以，5不可能和3的另一边子树相交
• 然后继续退回路径，进入父节点6所在的绿色方框里面，由于5和6之间的距离小于等于最近邻距离，所以，5可能在6的另一边子树里面找到更小距离点，进入6的另一边子树9
• 然后进入9所在的蓝色方框，由于5和9之间的距离大于最近邻，所以终止算法
• 由于我们迭代时记录返回路径中的最近邻点，所以最终输出6

根据上述思路，我们可以写出代码

def kdSearch(root, target):
    nearestDist = False
    nearestPoint = target
    
    def search(node, target):
        nonlocal nearestDist
        nonlocal nearestPoint
        
        if not node:
            return 
        
        # 步骤1：递归找到叶子节点
        if target <= node.data: # 进入左子树
            search(node.left, target)
        else: # 进入右子树
            search(node.right, target)
        
        #已经找到叶子节点，进入步骤2
        #其实上面的过程已经是在递归返回了
        
        # 计算当前节点与target之前的距离，并更新最近邻距离和最近邻点
        if not nearestDist:
            nearestDist = abs(target - node.data)
            nearestPoint = node.data
        elif nearestDist >= abs(target - node.data):
            nearestDist = abs(target - node.data)
            nearestPoint = node.data
        
        # 判断是否需要进入该节点的另一边子树
        if nearestDist >= abs(target - node.data):
            # 需要进入
            # 这里需要注意，按照target递归向下路径，当target<= node.data时，
            # 它实际上已经走过了node的左子树，所以另一边子树应该是右子树
            if target <= node.data:
                search(node.right, target)
            else:
                search(node.left, target)
        
    
    search(root, target)
    return nearestPoint

# 测试
nums = [3, 6, 2, 9, 10, 7, 4]
target = 5

# 生成kd树
root = kdTree(0, len(nums)-1)
# kd树搜索
print('值', target, '的最近邻是', kdSearch(root, target))

值 5 的最近邻是 6

这里是一维数组的情形，多维数据情形类似，后面有机会补上！
更一般的情形，可以参考大佬@火烫火烫的的代码，他做了多维情形下的最近邻代码；可以继续看大佬@晨语凡心
的博客，里面给出了多维情形下的k近邻代码。

下一篇博客将介绍 朴素贝叶斯决策。