Artistic style transfer for videos(译—视频的艺术风格迁移)
摘要
过去,手工重绘一副艺术风格的图像需要专业的艺术家和很长的时间,重绘视频序列更是无法想象。现在使用计算机使其成为可能,我们提出了一种方法,将风格从一张图片转移到整个视频序列。我们利用最近静态图片风格转移的最新进展,并提出适用于视频的新初始化和损失函数。这使我们能够生成一致且稳定的风格化视频序列,即使在具有大运动和强遮挡的情况下也是如此。我们表明,所提出的方法在质量和数量上明显优于更简单的baseline。
Introduction
最近对使用深度神经网络的样式转移问题做出了许多有趣的贡献。Gatys [3]提出了一种新的方法,使用神经网络捕捉艺术图像的风格,并将其转移到现实世界的照片。他们的方法使用来自VGG卷积网络[10]隐藏层的图像的高级特征表示来分离和重新组合内容和风格。这是通过制定优化问题来完成的,从白噪声开始,优化白噪声图片与内容图片有相似的神经元激活以及与风格图像有相似的特征相关性(用Gram矩阵来表示)。
本文以Gatys等人的方法为基础[3]并将风格转移扩展到视频序列。给定一副艺术图片,我们转移特点的风格到整个视频中。如果将视频每一帧独立的转换,会由于转换的不稳定性导致视频播放的闪烁和不连贯。为了规范转化并保持视频的各个帧之间的平滑过渡,我们引入了时间约束,用于惩罚两帧之间的偏差。时间约束考虑了来自原始视频的光流:不是惩罚与前一帧的偏差,而是惩罚沿点轨迹的偏差。遮挡区域和运动边界对其进行偏差惩罚。这允许该过程重建被遮挡区域和扭曲的运动边界,同时保留图像其余部分的外观,见图1。

此外对我们的方法提出了两种扩展,第一是使其可以在更长的时间里提高一致性;当在某个帧中被遮挡并且稍后被解除遮挡的区域在该过程中被重建时,该区域很可能具有与遮挡之前不同的外观。为了解决这个问题,我们使用了长期运动估计。这允许我们在遮挡之前和之后强制合成帧的一致性
第二风格转移往往会在图像边界处产生伪影。对于静态图像,这些伪影几乎不可见,但对于具有强相机运动的视频,它们朝向图像的中心移动并被放大。我们开发了一种多通道算法,该算法使用前向和后向流以交替方向处理视频。这会产生更连贯的视频。
我们在Sintel基准测试中结合不同的光流算法定量评估了我们的方法。此外,我们还展示了几部电影的定性结果。我们能够成功消除大部分时间伪影,并可以创建流畅和连贯的风格化视频。
相关工作
-
使用深度网络进行风格转移:Gatys等人 [3]通过使用VGG-19深度神经网络进行风格转移得到了显着的结果。各种后续论文采用了他们的方法,其中提出了不同的方式来表示神经网络中的风格。Li等人 [5]提出了一种保留风格图像的局部模式的方法。 他们使用神经元激活块来表示风格而不是使用Gram矩阵这样的全局表示。Nikulin等人 [7]尝试了Gatys等人的风格转移算法,在除了VGG之外的其他网络上的效果,并提出了图像风格表示方式的几种变化,以存档不同的目标,如照明或季节转移。但是,我们不知道有任何将此风格传输应用于视频的工作。
-
彩绘动画:创建具有艺术风格的视频序列的一种常见方法是生成人工画笔笔划以重新绘制场景。通过修改这些画笔笔划的各种参数(如厚度)或使用不同的画笔放置方法,可以获得不同的艺术风格。为了实现时间一致性,Litwinowicz [6]是最早使用光流的人之一。在他的方法中,为第一帧生成画笔笔划,然后沿着流场移动。后来,这种方法得到了改进,Hays 等人[4]为画笔笔划提出了新的文体参数,以模仿不同的艺术风格。O’Donovan等 [8]针对画笔笔划的最佳放置和形状制定了能量优化问题,并且还通过惩罚与前一帧相比的画笔笔划的形状和宽度的变化,将时间约束集成到优化问题中。这些方法在思想上与我们正在做的相似,但它们只能应用一种受限制的艺术风格。
静态图像中的风格迁移
这一节主要回顾Gatys[3]等人的方法,可参考:http://
视频中的风格迁移
我们使用以下记号: p ( i ) p^{(i)} p(i)表示原始视频的第i帧, a a a是风格图片, x ( i ) x^{(i)} x(i)是风格化后的帧,此外我们使用 x ′ ( i ) x'^{(i)} x′(i)表示第i帧的风格化算法初始图像, x j x_j xj表示向量的第j个部分。
初始化的短期一致性
当连续帧的样式传输由独立的高斯噪声初始化时,视频的两帧会聚到不同的局部最小值,导致视频强烈的抖动。最基础的产生时间一致的方法是使用第i帧风格化后的图片作为i+1帧的初始化。这样可以使两帧图片中一样的区域不改变,而剩下的区域使用优化函数转换。如果场景中存在物体运动,则这种简单的方法效果不佳,因为移动对象的初始化不正确。因此我们考虑光流以及使用前一帧的风格图片作为当前帧的初始化 x ′ ( i + 1 ) = w i ( i + 1 ) ( x ( i ) ) x'^{(i+1)}=w_i^{(i+1)}(x^{(i)}) x′(i+1)=wi(i+1)(x(i)),其中 w i ( i + 1 ) w_i^{(i+1)} wi(i+1)表示使用在图像 p i p^i pi和 p ( i + 1 ) p^{(i+1)} p(i+1)之间估计的光流场扭曲给定图片的函数。当然第一帧的风格化是需要随机初始化的。
我们尝试了两种最先进的光流估计算法,DeepFlow [12] 和 EpicFlow[9],都是基于深度匹配[12]:DeepFlow将其与变分方法相结合,而EpicFlow依赖于边缘保留稀疏到密集插值。
时序一致损失
为了在相邻帧之间实施更强的一致性,我们引入了显示的一致性惩罚到损失函数中。这需要检测不被遮挡的区域和运动边界。为了检测不被遮挡的区域,我们对光流进行前后一致性检查[11]。记 w = ( u , v ) w=(u,v) w=(u,v)是前向方向的光流, w ^ = ( u ^ , v ^ ) \widehat{w} = (\widehat{u}, \widehat{v}) w =(u ,v )s是后向方向的光流,记 w ~ \widetilde{w} w 为向前扭曲到第二个图像:
w ~ ( x , y ) = w ( ( x , y ) + w ^ ( x , y ) ) \widetilde{w}(x, y) = w((x,y) + \widehat{w}(x, y)) w (x,y)=w((x,y)+w (x,y))
在没有遮挡的情况下,这种扭曲的流动和后向流动大致相反。因此我们记满足下列不等式的区域为不遮挡区域:
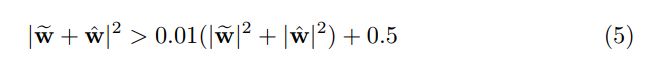
使用以下不等式检测运动边界:
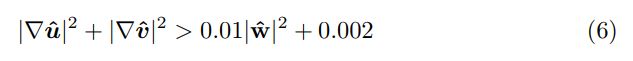
上述公式的系数取自[11]。
时间一致性损失函数在光流一致且高可信度估计的区域中惩罚与扭曲图像的偏差:

其中![]() 表示每个像素对于损失的权重, D = W × H × C D = W\times{H}\times{C} D=W×H×C表示图片的维度。我们定义在第i和i-1帧之间的权重 c ( i − 1 , i ) c^{(i-1, i)} c(i−1,i):0是在没有遮挡的区域(由前后向一致性检测)和运动边界,其他地方是1。可以使用0和1之间的潜在权重来结合光流预测的确定性。整体损失采用以下损失:
表示每个像素对于损失的权重, D = W × H × C D = W\times{H}\times{C} D=W×H×C表示图片的维度。我们定义在第i和i-1帧之间的权重 c ( i − 1 , i ) c^{(i-1, i)} c(i−1,i):0是在没有遮挡的区域(由前后向一致性检测)和运动边界,其他地方是1。可以使用0和1之间的潜在权重来结合光流预测的确定性。整体损失采用以下损失:
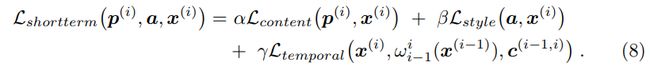
我们一帧一帧地优化,因此 x ( i − 1 ) x^{(i-1)} x(i−1)指的是已经风格化的i-1帧。
此外,我们尝试了更稳健的绝对误差,而不是时间一致性损失的平方误差;结果显示在第二部分。
长期一致性
短期模型有以下限制:当某些区域在某些帧中被遮挡而后来又出现时,这些区域可能会改变它们在风格化视频中的外观。这可以通过长期动作来抵消。不仅惩罚与前一帧的差距,而考虑更远的帧。记 J J J表示需要考虑的帧的集合,例如 J = { 1 , 2 , 4 } J={\{1,2,4\}} J={1,2,4}表示第i帧考虑第 i − 1 i-1 i−1、 i − 2 i-2 i−2、 i − 4 i-4 i−4帧。具有长期一致性损失函数如下:
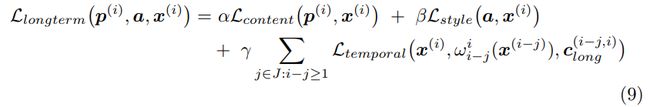
记 c ( i − j , i ) c^{(i-j, i)} c(i−j,i)是i-j和第i帧之间的光流,和短期一致的定义一样。因此 c l o n g ( i − j , i ) c^{(i-j, i)}_{long} clong(i−j,i)计算为:
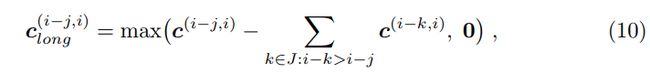
这意味着我们首先应用通用的短期一致性,对于处于不被遮挡区域的像素,我们会查看过去,直到找到一个具有一致对应的帧。简单地使用 c ( i − j , i ) c^{(i-j,i)} c(i−j,i)的优点是每个像素仅连接到距离最近的可能帧。由于在更多帧上计算的光流比在更少的帧上计算更加错误,因此产生更流畅的视频。
Multi-pass 算法
我们发现输出图像倾向于具有较小的对比度并且在图像边界附近比在图像的其他区域中更不多样化。对于大多数静态视频,此效果几乎看不出来。然而,在强烈的相机运动的情况下,来自图像边界的区域朝向图像的中心移动,当与我们的时间约束结合时,这导致较低的图像质量。因此,我们开发了一种Multi-pass算法,该算法以多次通过和交替方向处理整个序列,基本思想是我们逐步向前和向后传播中间结果,避免从图像边界到中心的单向信息流。
每次传递都包含相对较少的迭代次数而没有完全收敛。在开始时,我们基于随机初始化独立地处理每个帧。之后,我们将帧与根据光流变形的先前帧的重叠部分混合,然后针对使用该混合初始化的一些迭代运行优化算法。处理序列的方向在每次通过中交替进行,我们重复这种混合和优化以实现融合。
我们记 x ′ ( i ) ( j ) x'^{(i)(j)} x′(i)(j)是i通过j的初始化帧, x ( i ) ( j ) x^{(i)(j)} x(i)(j)是对应帧经过一些迭代优化后的输出帧。在正向处理时,帧i的初始化创建如下:
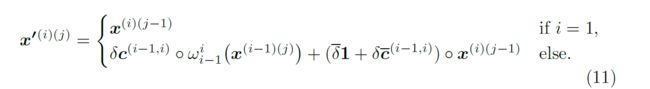
这里o操作表示向量元素相乘, δ \delta δ和 δ ˉ = 1 − δ \bar{\delta}=1-\delta δˉ=1−δ是混合因子,1表示向量元素全是1, c ˉ = 1 − c \bar{c}=1-c cˉ=1−c。
类似地,反向传递的初始化是:
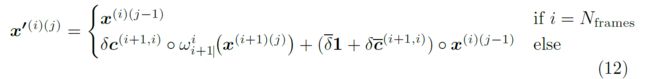
多遍算法可以与上述时间一致性损失组合。当我们在几个初始通道中禁用时间一致性损失时,我们取得了良好的结果,并且仅在图像稳定后才在后续通道中启用它。