阅读Hierarchical Graph Representation Learning with Differentiable Pooling(NeurIPS 2018)

  最近关注graph pooling，Hierarchical Graph Representation Learning with Differentiable Pooling(NeurIPS 2018)，分层可微pooling图表示学习方法。

Abstract

  近年来，图神经网络（GNNs）通过有效的学习节点embeddings，使图表示学习发生了革命性的变化，在节点分类、链路预测等任务中取得了最新的成果。然而，当前的GNN方法本质上是在平面上(flat)的，并且不能学习图的层次表示，这一限制对于图分类任务来说，对结果影响关键。其中的目标是预测与整个图相关联的标签。文中提出了DIFFPOOL模型，一个可微的图pooling模块，它可以生成图的层次表示，并且可以end-to-end与各种图神经网络结构相结合。DIFFPOOL为一个深度GNN的每一层节点学习一个可微的soft cluster assignment，将节点映射到一组cluster，然后形成下一个GNN层的粗化输入(coarsened input)。实验结果表明，与所有现有的pooling方法相比，将现有的GNN方法与DIFFPOOL方法相结合，在图形分类benchmarks上平均提高了5-10%的准确性，在五个benchmarks数据集中有四个达到了SOTA的水平。

1 Introduction

  当前GNN体系结构的一个主要限制是它们本质上是flat的，因为它们只在图的edge传播信息，不能以分层的方式推断和聚合信息。例如，为了成功地编码有机分子的图形结构，人们理想地希望编码局部分子结构（例如，单个原子和他们的直接关系)以及分子图的粗粒度结构（例如，表示分子中功能单元的原子群和键）。缺少层次结构对于图分类任务来说是非常有问题的，因为它的目标是预测与整个图相关联的标签。将GNNs应用于图分类时，标准方法是为图中的所有节点生成嵌入，然后将所有这些节点嵌入全局地汇集在一起，例如，使用简单的求和或在集合上操作的神经网络。这种全局池方法忽略了图中可能存在的任何层次结构，并且它阻止研究人员为整个图上的预测任务构建有效的GNN模型。
  作者提出DIFFPOOL，一个可微的图pooling模块，它可以以分层和端到端的方式适应各种图神经网络结构（图1）。DIFFPOOL允许开发更深入的GNN模型，这些模型可以学习在图的层次表示上操作。作者开发了一个CNNs中空间池操作的图形模拟，它允许深层CNN架构在图像的粗糙表示迭代操作。与标准cnn相比，GNN设置的挑战在于，图不包含空间局部性的自然概念，即不能简单地将图上“m×m块”中的所有节点聚集在一起，因为图的复杂拓扑结构排除了对“块”的任何直接、确定的定义。此外，与图像数据不同，图形数据集通常包含节点数和边数不同的图形，这使得定义一般的图形池运算符变得更加困难。

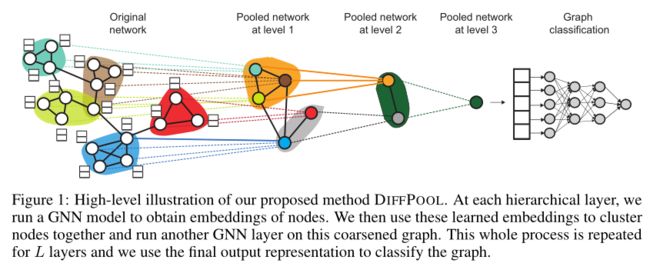
  为了解决上述问题，我们需要一个模型来学习如何将节点聚集在一起，从而在底层图的顶部构建一个层次化的多层scaffold(脚手架)。DIFFPOOL在一个深度GNN的每一层学习一个可微的 soft assignment，根据节点的学习嵌入将节点映射到一组clusters。在这个框架中，我们通过以分层方式“堆叠”GNN层来生成深层GNN（图1）：第$l$层GNN模块的输入节点对应于第$l-1$层GNN模块学习到的集群clusters。因此，DIFFPOOL的每一层都越来越粗化(clusters)输入图，DIFFPOOL能够在训练后生成任意输入图的层次表示。我们表明DIFFPOOL可以与各种GNN方法相结合，在五分之四的benchmark分类任务中，平均提高了7%的精度，并达到了新的水平。最后，我们证明DIFFPOOL可以学习可解释的层次clusters,这些clusters对应于输入图中定义良好的节点聚群。

• hard assignment：每个数据点都归到一个类别(i.e. cluster)。
• soft assignment：把数据点归到不同的类，分到每个类有不同的概率。
• assignment：文中涉及的assignment就是把节点分类、归类的意思。
• hierarchical：分层的，层次化的，就是指类似CNN中的分层提取特征，把相同的点聚在一起，用一个点表示。传统的方式是先使用GN求出图中所有节点的embedding，然后使用全局地使用一层网络进行pooling操作，而文中使用了多层pooling。

2 Related Work

  文中工作建立在最近关于图神经网络和图分类的大量(rich line of)研究的基础上。

  GNNs被广泛应用于各种任务中，包括节点分类、链路预测、图分类和化学信息学中。在图分类的任务中，应用GNNs的一个主要挑战是从节点embedding到整个图的表示。解决这一问题的常见方法有：
1.简单地在最后一层中将所有节点embedding求和（Convolutional networks on graphs for learning molecular fingerprints，NIPS 2015）；
2.引入一个连接到图中的所有节点的“虚拟节点”来求平均值（Gated graph sequence neural networks，ICLR 2016）；
3,使用深度学习架构来聚合节点embedding（Neural message passing for quantum chemistry，ICML 2017）。
  然而，所有这些方法都有其局限性，即它们不能学习层次结构表示(即，所有节点的embedding都在一个单层中被pool)，因此无法捕获许多真实世界中的图的结构。
  最近的一些方法也提出了将CNN架构应用于连接（concatenate）所有节点的embedding：

• [PATCHY-SAN] Learning convolutional neural networks for graphs，ICML 2016；
• An end-to-end deep learning architecture for graph classification，AAAI 2018

但这些方法需要学习节点的排序，这通常是非常困难的，相当于求解图同构。

最后，有一些工作通过结合GNNs和确定性图聚类算法来学习层次图表示：

• Convolutional neural networks on graphs with fast localized spectral filtering，NIPS 2016；
• SplineCNN: Fast geometric deep learning with continuous B-spline kernels，CVPR 2018；
• Dynamic edge-conditioned filters in convolutional neural networks on graphs，CVPR 2017
  与这些方法不同，DIFFPOOL寻求以端到端的方式学习图的层次结构，而不依赖于确定性的图聚类程序。

3 Proposed Method

  DIFFPOOL的核心思想是，它通过向层次化的pool图节点提供一个可微模块，实现了深层、多层GNN模型的构建。在本节中，我们概述了DIFFPOOL模块，并展示了它是如何在一个深层GNN架构中应用。

3.1 Preliminaries

  图G表示为(A,F)，其中$A\in \{0,1{\}}^{n\times n}$是邻接矩阵，$F\in {\mathbb{R}}^{n\times d}$是假设每个节点都有d个特征节点的特征矩阵。一组标记图为$D=(G_1,y_1),(G_2,y_2),...$其中图分类的目标是学习将图映射到标签集的映射$f:G\to Y$
Graph neural networks
$$H^{(k)}=M(A,H^{(k-1)};{\theta }^{(k)})(1)$$其中，$H^{(k)}$表示第k个隐含层，M是消息传播函数，比如RELU等。${\theta }^{(k)}$trainable parameters。$H^{(0)}=X$,初始值为输入值特征。
Stacking GNNs and pooling layers堆叠GNNs和pooling层
文中的目标是定义一种通用，端到端，可微的策略，使得可以用一种层次化的方式堆叠多层GNN模型。

给定一个GNN模块的输出$Z=GNN(A，X)$和一个图的邻接矩阵$A\in {\mathbb{R}}^{n\times n}$ ，目标是寻找一种方式可以得到一个新的包含m$A^{\prime }\in {\mathbb{R}}^{m\times m}$ ，节点embedding矩阵为$Z^{\prime }\in {\mathbb{R}}^{m\times d}$ 。

这个新的粗化图（coarsened graph）作为下一层GNN的输入，重复L次就可到了一系列的coarser。因此，目标就是需要学习一种pooling策略，这种策略可以泛化到具有不同节点、边的图中，并且能够在推理过程中能适应不同的图结构。

3.2 Differentiable Pooling via Learned Assignments

  DIFFPOOL方法通过使用GNN模型的输出学习节点上的cluster assignment matrix来解决上述问题。
Pooling with an assignment matrix我们将$l$层的cluster assignment matrix表示为$S^{(l)}\in {\mathbb{R}}^{n_l\times n_{l+1}}$。$S^{(l)}$的每行对应于层$l$上的$n_l$节点（或clusters），$S^{(l)}$的每列对应于下一层$l+1$上的$n_{l+1}$ clusters之一。直观地说，$S^{(l)}$将层l上的每个节点soft assignment 给下一个粗化层l+1中的clusters。
  假设$S^{(l)}$已经计算好了，也就是说，我们已经计算了模型第l层的矩阵。我们将该层的输入邻接矩阵表示为$A^{(l)}$，将该层的输入节点嵌入矩阵表示为$Z^{(l)}$。给定这些输入，DIFFPOOL层$(A^{(l+1)},X^{(l+1)})=DIFFPOOL(A^{(l)},Z^{(l)})$对输入图进行粗化，为粗化图中的每个节点/clusters生成新的粗化邻接矩阵$A^{(l+1)}$和新的嵌入矩阵$X^{(l+1)}$。特别是，我们应用以下两个方程$$X^{(l+1)}=S^{(l{)}^T}{Z}^{(l)}\in {\mathbb{R}}^{n_{l+1}\times d}(3)$$$$A^{(l+1)}=S^{(l{)}^T}{A}^{(l)}{S}^{(l)}\in {\mathbb{R}}^{n_{l+1}\times n_{l+1}}(4)$$方程(3)取节点嵌入$Z^{(l)}$并根据cluster assignments $S^{(l)}$聚合这些嵌入，为$n_{l+1}$集群中的每个集群生成嵌入。类似地，方程(4)采用邻接矩阵$A^{(l)}$并生成表示每对clusters之间的连接强度的粗糙邻接矩阵。
  通过方程(3)和(4)，DIFFPOOL层使图粗化：下一层邻接矩阵$A^{(l+1)}$表示具有$n_{l+1}$个节点或cluster的粗化图，其中新粗化图中的每个cluster节点对应于图中位于$l$层的一个cluster节点。注意$A^{(l+1)}$是一个实矩阵，表示完全连接边加权图；每个条目$A_{ij}^{(l+1)}$可以看作是cluster i和cluster j之间的连接强度。同样，$X^{(l+1)}$的第i行对应于cluster i的嵌入。粗化的邻接矩阵$A^{(l+1)}$和cluster 嵌入$X^{(l+1)}$可以一起用作到另一个GNN层的输入，我们在下面详细描述的过程。
Learning the assignment matrix下面我们将描述DIFFPOOL的体系结构，即DIFFPOOL如何生成assignment matrix $S^{(l)}$和嵌入矩阵$Z^{(l)}$，这些矩阵用于等式(3)和(4)。我们使用两个独立的gnn生成这两个矩阵，这两个gnn都应用于输入cluster 节点特征$X^{(l)}$和粗化邻接矩阵$A^{(l)}$。在l层嵌入GNN是应用于这些输入的标准GNN模块:$$Z^{(l)}=GN{N}_{l,embed}(A^{(l)},X^{(l)})(5)$$例如，我们取l层 cluster nodes之间的邻接矩阵（从等式4）和pooled features for the clusters（从等式3）通过标准GNN得到clusters节点的新嵌入$Z^{(l)}$。相反，层l的pooling GNN使用输入cluster features $X^{(l)}$和cluster adjacency matrix $A^{(l)}$来生成assignment matrix:$$S^{(l)}=softmax(GN{N}_{l,pool}(A^{(l)},X^{(l)}))$$其中softmax函数按行应用。$GN{N}_{l,pool}$的输出维度对应于层l中预定义的最大cluster 数，是模型的一个超参数。
  注意，这两个GNN使用相同的输入数据，但具有不同的参数化并扮演不同的角色：嵌入GNN为该层的输入节点生成新的嵌入，而池GNN生成输入节点到$n_{l+1}$clusters的概率assignment(分配)。
  在基本情况下，层l＝0的方程（5）和方程（6）的输入仅仅是原始图的输入邻接矩阵A和节点特征F。在使用DIFFPOOL的深度GNN模型的倒数第二层L-1处，我们将分配矩阵$S^{(L-1)}$设置为1的向量，即，最后一层L处的所有节点被分配到单个cluster，生成与整个图对应的最终嵌入向量。最后的输出嵌入可以作为可微分类器（如softmax层）的特征输入，整个系统可以使用随机梯度下降进行端到端的训练。
Permutation invariance置换不变性。注意，为了对图分类有用，pooling层在节点置换下应该是不变的。对于DIFFPOOL，我们得到了如下的正结果，这表明任何基于DIFFPOOL的深GNN模型都是置换不变的，只要组件GNN是置换不变的。
Proposition 1…设$P\in \{0,1{\}}^{n\times n}$为任意置换矩阵，则只要$GNN(A，X)=GNN(PA{P}^T,X)，DIFFPOOL(A,Z)=DIFFPOOL(PA{P}^T,PX)$（即只要所使用的GNN方法是置换不变的）
证明。方程（5）和（6）在GNN模是置换不变的假设下是置换不变的。由于任何置换矩阵都是正交的，将$P^{T}P=I$应用于方程（3）和（4）就完成了证明。

3.3 Auxiliary Link Prediction Objective and Entropy Regularization辅助链路预测目标与熵正则化

  在实际应用中，仅使用图形分类任务中的梯度信号很难训练pooling GNN（等式4）。直观地说，我们有一个非凸优化问题，并且在训练初期很难将pooling GNN从局部极小值中优化。为了缓解这个问题，我们训练了带有辅助链路预测目标的池GNN，它编码了附近节点应该被一起池化的intuition。特别是，在每一层l，我们最小化$L_{LP}=||A^{(l)},S^{(l)}S(l{)}^T|{|}_F$，其中$||\cdot |{|}_F$表示Frobenius范数。注意，较深层的邻接矩阵$A^{(l)}$是下层assignment矩阵的函数，在训练过程中会发生变化。池GNN（等式4）的另一个重要特征是，每个节点的output cluster assignment通常应接近one-hot向量，以便清楚地定义每个集群或子图的成员。因此，我们通过最小化$L_E=\frac{1}{n}{\sum }_{i=1}^{n}H(S_i)$来正则化cluster的熵，其中H表示熵函数，$S_i$是S的第i行。在训练过程中，每一层的$L_{LP}$和$L_E$被加入到分类损失中。在实践中，我们观察到，带有次要目标的训练需要更长的时间来收敛，但是仍然可以获得更好的性能和更易于解释的集群分配。
其他部分参看博客