【时空序列预测第十篇】Cubic LSTMs for Video Prediction

一、Address

AAAI2019的一篇文章

Cubic LSTMs for Video Prediction

论文链接地址: https://arxiv.org/pdf/1904.09412.pdf

二、Introduction and Model

2.1 LSTM以及ConvLSTM

这里简单列举下，其实我已经写过很多次了，只是为了方便大家阅读

LSTM结构具体参考文章：

公式为：
$$\mathrm{F}\mathrm{C}-\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\{\begin{array}{l}{i}_t=\sigma \left({\mathcal{W}}_i\cdot \left[{\mathcal{X}}_t,{\mathcal{H}}_{t-1}\right]+b_i\right)\\ f_t=\sigma \left({\mathcal{W}}_f\cdot \left[{\mathcal{X}}_t,{\mathcal{H}}_{t-1}\right]+b_f\right)\\ o_t=\sigma \left({\mathcal{W}}_o\cdot \left[{\mathcal{X}}_t,{\mathcal{H}}_{t-1}\right]+b_o\right)\\ c_t=\tanh \left({\mathcal{W}}_c\cdot \left[{\mathcal{X}}_t,{\mathcal{H}}_{t-1}\right]+b_c\right)\\ {\mathcal{C}}_t=f_t\odot {\mathcal{C}}_t+i_t\odot c_t\\ {\mathcal{H}}_t=o_t\odot \tanh \left({\mathcal{C}}_t\right)\end{array}$$

缩写可以表示为：
$$\begin{array}{l}\mathrm{F}\mathrm{C}-\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}:\\ \left({\mathcal{C}}_t,{\mathcal{H}}_t\right)=\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\left({\mathcal{X}}_t,\left({\mathcal{C}}_{t-1},{\mathcal{H}}_{t-1}\right);\mathcal{W},b;\cdot \right)\end{array}$$

ConvLSTM论文解读具体参考文章：

缩写可以表示为：

$$\left({\mathcal{C}}_t,{\mathcal{H}}_t\right)=\mathrm{LSTM}\left({\mathcal{X}}_t,\left({\mathcal{C}}_{t-1},{\mathcal{H}}_{t-1}\right);\mathcal{W},b;\ast \right)$$

2.2 CubicLSTM

2.2.1 结构

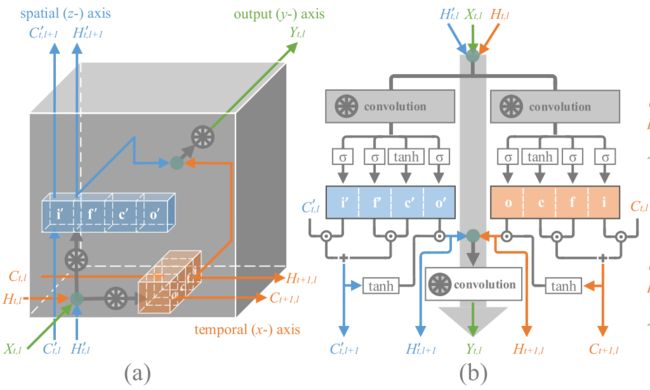
左面是一个立体图，很难看明白其中的结构，咱们主要看右边的b，拓扑图。

整理的cell最主要的特点是将temporal和spatial的信息分开处理，即左图中的sptial axis和temporal axis两个轴方向。

CnbicLSTM包括三个branch：temporal branch， spatial branch， output branch，顾名思义temporal branch主要是获得动作的，也就是目标之间的变化即时间的运动信息，spatial branch主要是获取本身目标的结构信息即目标空间信息，output branch就是把二者做了个整合，之后输出prediction

再仔细看一下结构，感觉不需要多说，这幅图画的很清楚了，大致来讲就是蓝色为spatial,橘黄色为temporal。
可以看到空间上，主要是layer的变化，也就是L->L+1，而时间上主要是step的变化，也就是t->t+1

大致说下流程，就是temporal的hidden state和spatial的hidden state以及输入x经过两个conv分别得到时间维度和空间维度的三个门控以及内部状态，之后接下来的各种操作和convLSTM里面基本上一样，最后得到两个hidden state经过conv得到最终的Yt

其实换一个角度本篇的这个结构本质上就是个两个convLSTM的拼接cell，只是生成门控的输入为三个值所决定的。

所以公式也很好得出。

2.2.2 公式

$$\text{ CubicLSTM }\{\begin{array}{l}\text{ temporal branch }:\left({\mathcal{C}}_{t,l},{\mathcal{H}}_{t,l}\right)=\mathrm{LSTM}\left({\mathcal{X}}_{t,l},{\mathcal{H}}_{t,l-1}^{\prime },\left({\mathcal{C}}_{t-1,l},{\mathcal{H}}_{t-1,l}\right);\mathcal{W},b;\ast \right)\\ \text{ spatial branch : }\left({\mathcal{C}}_{t,l}^{\prime },{\mathcal{H}}_{t,l}^{\prime }\right)=\mathrm{LSTM}\left({\mathcal{X}}_{t,l},{\mathcal{H}}_{t-1,l},\left({\mathcal{C}}_{t,l-1}^{\prime },{\mathcal{H}}_{t,l-1}^{\prime }\right);{\mathcal{W}}^{\prime },b^{\prime };\ast \right)\\ \text{ output branch : }{\mathcal{Y}}_{t,l}={\mathcal{W}}^{\prime \prime }\ast \left[{\mathcal{H}}_{t,l},{\mathcal{H}}_{t,l}^{\prime }\right]+b^{\prime \prime }\end{array}$$

2.2.3 Cubic RNN

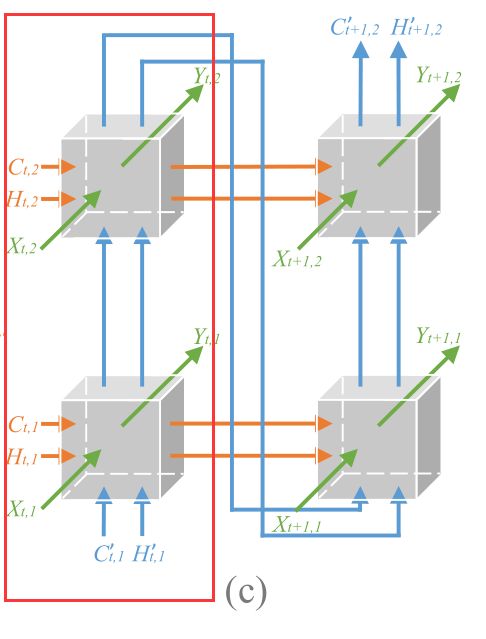
这种rnn的提出少不了stacking结构。

我们先看个细节图，玩多了rnn的应该都清楚一般来说temporal的轴线，也就是time step的逐步处理的时候temporal的参数肯定是共享的。

所以下图其实就是一个两层的结构，即红框中的结构

除了这个以外，在spatial上叠加几层，也是为了让objection的信息更加突出，得到更好的空间信息。
并且前一步的spatial的信息会传给下一步的最初的层，即蓝色线部分。

这个输入设计的就很有趣了，因为层数主要代表的是spatial，如图这么输入的话也就是说每层考虑了之前的临近的objection的信息，相当于多了一些目标的信息，这个输入称之为slide window。

预测规律如图所示。

这个结构总体来讲就很有趣了，看着像个立体的网

三、Experiments

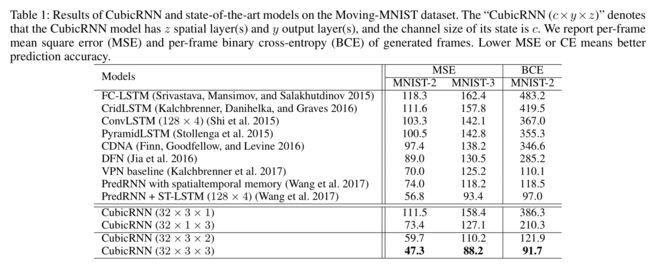
还是做得Moving MNIST数据集，和predrnn++做的类似，应用了三个数字和两个数字的序列图，以及应用了mse和bce两个评价指标

也做了一些可视化工作。

四、Conclusions

1. 文中其实强调了很多次convlstm的目前无法动摇的地位，之后决定在convlstm上做创新，想到的点子出发点就是如何把temporal和spatial分开
2. 分开之后分别得到c和h，经过前后各一个conv得到门控和c以及最终融合h得到最终的prediction
3. 把结构设计为了一个立体的结构，和平时的平面有一些不同，所以在stacking的时候会感觉像一个立体的网一样的结构