支持向量机学习笔记
目录
- 支持向量机
- 一、感知机和支持向量机的关系
- 二、决策函数
- 三、二次规划以及硬间隔和软间隔分类问题
- 3.1线性可分支持向量机与硬间隔最大化
- 3.1.1硬间隔分类
- 3.1.1.1硬间隔线性SVM分类器的目标
- 3.2 线性支持向量机与软间隔最大化
- 3.2.1 软间隔分类
- 3.2.1.1软间隔线性SVM分类器的目标
- 3.3小结
- 四、对偶问题(待优化)
- 五、核化SVM
- 问题
- 1. 支持向量的基本思想是什么?
- 2. 什么是支持向量?
- 3. 使用SVM时,对输入值进行缩放为什么重要?
- 4. SVM分类器在对实例进行分类时,会输出信心分数么?概率呢?
- 5. 针对于线性SVM,假设训练集有上千万个实例和几百个特征,你应该使用SVM原始问题还是对偶问题来训练模型?
- 6. 假设用RBF核训练一个SVM分类器,看起来似乎对训练集你和不足,应该如何调整 γ \gamma γ参数和 C C C参数?
- SMO(Sequential Minimal Optimization)序列最小优化算法
- 一、算法目标
- 二、算法工作原理
- 三、算法代码
支持向量机
一、感知机和支持向量机的关系
在感知机的基础上,为了得到唯一的超平面,需要对分离超平面增加约束条件,这就是线性支持向量机的想法。
感知机学习算法的原始形式和对偶形式与支持向量机学习算法的原始形式和对偶形式相对应
优点:泛化错误率低,计算开销不大,结果易解释
缺点:对参数调节和核函数的选择敏感,原始分类器不加修改仅适用于处理二分类问题
适用数据类型:数值型和标称型数据
二、决策函数
决策函数: h = w T ⋅ x + b h=\mathbf w^T\cdot \mathbf x+b h=wT⋅x+b
决策边界:决策函数等于零的集合,是两个平面的交集,也就是一条直线
更概括的说,当有 n n n 个特征时,决策函数是一个 n n n 维的超平面,决策边界是一个 n − 1 n-1 n−1 维的超平面
决策函数的斜率 = = = 权重向量 w w w 的范数 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣
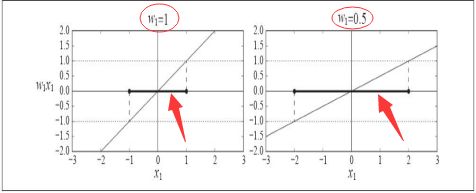
权重向量的范数越小,间隔越大,比如斜率除以2,相应的权重向量的范数也就缩小了一倍,而决策函数等于 ± 1 \pm 1 ±1 的点也将离决策函数两倍远,即相当于间隔乘以2,如图:
三、二次规划以及硬间隔和软间隔分类问题
硬间隔和软间隔问题都属于线性约束的凸二次优化问题,统称为二次规划(QP)问题
意思就是二次规划是爸爸,硬间隔和软间隔是儿子
二次规划问题:
最小化 p 1 2 p T ⋅ H ⋅ p + f T ⋅ p 使得 A ⋅ p ≤ b 其中 { p 是一个 n p 维向量 ( n p 为参数数量 ) H 是一个 n p × n p 矩阵 f 是一个 n p 维向量 A 是一个 n c × n p 矩阵 ( n c 为约束数量 ) b 是一个 n c 维向量 {\mathop{\text{最小化}}\limits_{\mathbf p}}\space{1\over2}\mathbf{p^T\cdot H\cdot p}+\mathbf{f^T\cdot p}\\\text{使得}\space\mathbf{A\cdot p \leq b}\\\text{其中}\space \begin{cases}\mathbf p\space\text{是一个}n_p\text{维向量}(n_p\text{为参数数量})\\ \mathbf H\space\text{是一个}n_p\times n_p\text{矩阵}\\ \mathbf f\space\text{是一个}n_p\text{维向量}\\ \mathbf A\space\text{是一个}n_c\times n_p\text{矩阵}(n_c\text{为约束数量})\\ \mathbf b\space\text{是一个}n_c\text{维向量}\end{cases} p最小化 21pT⋅H⋅p+fT⋅p使得 A⋅p≤b其中 ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧p 是一个np维向量(np为参数数量)H 是一个np×np矩阵f 是一个np维向量A 是一个nc×np矩阵(nc为约束数量)b 是一个nc维向量
给二次规划的参数按特定方式设置,就可以实现硬间隔和软间隔线性SVM分类器的目标,这不是初学SVM要纠结的问题,所以具体如何设置就不细讲
3.1线性可分支持向量机与硬间隔最大化
线性可分支持向量机定义:给定线性可分训练数据集,通过间隔最大化或
等价地求解相应的凸二次规划问题学习得到的分离起平面为:
w ∗ ⋅ x + b ∗ = 0 w^*\cdot x+b^*=0 w∗⋅x+b∗=0
以及相应的分类决策函数
f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ ) f(x) = sign(w^*\cdot x+b^*) f(x)=sign(w∗⋅x+b∗)
称为线性可分支持向量机
3.1.1硬间隔分类
严格地让所有实例都不在间隔内,并且位于正确的一边,也就是避免间隔违例
缺陷:
1.只在数据线性可分离时有效
2.对异常值非常敏感
3.1.1.1硬间隔线性SVM分类器的目标
最小化 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 得到尽可能大的间隔,同时避免任何间隔违例(硬间隔),即所有训练集的实例都要被正确分类,正类训练集的决策函数大于1,负类训练集的决策函数小于-1
现定义:
t ( i ) = { + 1 ( y i = 1 , 即实例为正类 ) − 1 ( y i = 0 , 即实例为负类 ) t^{(i)}=\begin{cases}+1&(y^i=1,\text{即实例为正类})\\-1&(y^i=0,\text{即实例为负类})\end{cases} t(i)={+1−1(yi=1,即实例为正类)(yi=0,即实例为负类)
则对所有正确分类的实例有:
t ( i ) ( w T ⋅ x ( i ) + b ) ≥ 1 ( i = 1 , 2 , . . . , m ) t^{(i)}(\mathbf w^T\cdot \mathbf x^{(i)}+b)\geq1\tag{$i=1,2,...,m$} t(i)(wT⋅x(i)+b)≥1(i=1,2,...,m)
由此将硬间隔线性SVM分类器的目标转化为了一个约束优化的问题,即:
最小化 w , b 1 2 w T ⋅ w {\mathop{\text{最小化}}\limits_{\mathbf w,b}}\space{1\over2}\mathbf w^T\cdot \mathbf w w,b最小化 21wT⋅w
具体是如何得到这个最后的约束优化?参考链接
1 2 w T ⋅ w = 1 2 ∣ ∣ w ∣ ∣ 2 {1\over2}\mathbf w^T\cdot \mathbf w={1\over2}||w||^2 21wT⋅w=21∣∣w∣∣2,之所以不是直接最小化 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣,是因为二者虽然会得到同样的结果,但是 1 2 ∣ ∣ w ∣ ∣ 2 {1\over2}||w||^2 21∣∣w∣∣2有一个简单好用的导数 w \mathbf w w,而 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 在 w = 0 \mathbf w=0 w=0 时是不可微的。优化算法在可微函数上的工作效率要好得多
3.2 线性支持向量机与软间隔最大化
3.2.1 软间隔分类
尽可能在保持间隔宽阔和限制间隔违例(即位于间隔之上甚至在错误的一边的实例)之间找到良好的平衡, s k l e a r n sklearn sklearn 的 S V C SVC SVC 类中的超参数 C C C 用来控制这个平衡, C C C 越小间隔越宽,间隔违例也就越多
3.2.1.1软间隔线性SVM分类器的目标
在硬间隔的基础上为每个实例引入一个松弛变量 ζ ( i ) ≥ 0 \zeta^{(i)}\geq0 ζ(i)≥0, ζ ( i ) \zeta^{(i)} ζ(i)衡量的是第 i i i 个实例允许间隔违例的程度
有两个互相冲突的目标:松弛变量 ζ ( i ) \zeta^{(i)} ζ(i)越小越好从而减少间隔违例,同时 1 2 ∣ ∣ w ∣ ∣ 2 {1\over2}||w||^2 21∣∣w∣∣2 最小化使得间隔增大,那么这时候就需要用到 S V M SVM SVM 类里的超参数 C C C:允许我们在两个目标之间权衡:
最小化 w , b , ζ 1 2 w T ⋅ w + C ∑ i = 1 m ζ ( i ) 使得 t ( i ) ( w T ⋅ x ( i ) + b ) ≥ 1 − ζ ( i ) 且 ζ ( i ) ≥ 0 ( i = 1 , 2 , . . . , m ) {\mathop{\text{最小化}}\limits_{\mathbf w,b,\zeta}}\space{1\over2}\mathbf w^T\cdot \mathbf w+C\sum_{i=1}^{m}\zeta^{(i)}\\\text{使得}\space t^{(i)}(\mathbf w^T\cdot \mathbf x^{(i)}+b)\geq1-\zeta^{(i)}\space\text{且}\space\zeta^{(i)}\geq0(i=1,2,...,m) w,b,ζ最小化 21wT⋅w+Ci=1∑mζ(i)使得 t(i)(wT⋅x(i)+b)≥1−ζ(i) 且 ζ(i)≥0(i=1,2,...,m)
3.3小结
- 当训练数据线性可分时,通过硬间隔最大化(Chard margin maximization)学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机
- 当训练数据近似线性可分时,通过软间隔最大化(soft margin maximization)也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机
- 当训练数据线性不可分时,通过使用核技巧(kernel trick) 及软间隔最大化,学习非线性支持向量机。
四、对偶问题(待优化)
- 原始问题:给定的约束优化问题
- 对偶问题:和原始问题不同但密切相关的问题
SVM的原始问题满足:目标函数是凸函数,且不等式约束是连续可微的凸函数
因此SVM的原始问题和对偶问题的解可以相同
线性SVM目标的对偶形式:
最小化 α 1 2 α ( i ) α ( j ) t ( i ) t ( j ) x ( i ) T ⋅ x ( j ) − ∑ i = 1 m α ( i ) 使得 α ( i ) ≥ 0 ( i = 1 , 2 , . . . , m ) {\mathop{\text{最小化}}\limits_{\mathbf \alpha}}\space{1\over2}\space\alpha^{(i)}\alpha^{(j)}t^{(i)}t^{(j)}\mathbf x^{(i)T}\cdot x^{(j)}-\sum_{i=1}^{m}\alpha^{(i)}\\\text{使得}\space\alpha^{(i)}\geq0(i=1,2,...,m) α最小化 21 α(i)α(j)t(i)t(j)x(i)T⋅x(j)−i=1∑mα(i)使得 α(i)≥0(i=1,2,...,m)
求得上式的 α ^ \hat\alpha α^之后就可以从对偶问题的解转到原始问题的解:
w ^ = ∑ i = 1 m α ( i ) t ( i ) x ( i ) \hat{w}=\sum_{i=1}^{m}\alpha^{(i)}t^{(i)}\mathbf x^{(i)} w^=i=1∑mα(i)t(i)x(i)
b ^ = 1 n s ∑ i = 1 , α ( i ) > 0 m ( 1 − t ( i ) ( w ^ T ⋅ x ( i ) ) ) \hat{b}={1\over n_s}\sum_{i=1,\alpha^{(i)}>0}^{m}(1-t^{(i)}(\hat{w}^T\cdot \mathbf x^{(i)})) b^=ns1i=1,α(i)>0∑m(1−t(i)(w^T⋅x(i)))
五、核化SVM
核函数(kernel function) :当输入空间为欧氏空间或离散集合、特征空间为希尔伯特空间时,核函数(kernel function) 表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。
核技巧(kernel trick):通过使用核函数可以学习非线性支持向量机,等价于隐式地在高维的特征空间中学习线性支持向量机。
核方法(kernel method): 比支持向量机更为一般的机器学习方法。
在SVM里面添加核技巧就叫核化SVM
举个例子
ϕ ( x ) = ϕ ( ( x 1 x 2 ) ) = ( x 1 2 2 x 1 x 2 x 2 2 ) (二阶多项式映射) \phi(x)=\phi\begin{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}\end{pmatrix}=\begin{pmatrix}x_1^2\\\sqrt{2}x_1x_2\\x_2^2\end{pmatrix}\tag{二阶多项式映射} ϕ(x)=ϕ((x1x2))=⎝⎛x122x1x2x22⎠⎞(二阶多项式映射)
ϕ ( a ) T ⋅ ϕ ( b ) = ( a 1 2 2 a 1 a 2 a 2 2 ) T ⋅ ( b 1 2 2 b 1 b 2 b 2 2 ) = a 1 2 b 1 2 + 2 a 1 b 1 a 2 b 2 + a 2 2 b 2 2 = ( a 1 b 1 + a 2 b 2 ) 2 = ( ( a 1 a 2 ) T ⋅ ( b 1 b 2 ) ) 2 = ( a T ⋅ b ) 2 \phi(\mathbf a)^T\cdot\phi(\mathbf b)= \begin{pmatrix}a_1^2\\\sqrt{2}a_1a_2\\a_2^2\end{pmatrix}^T\cdot \begin{pmatrix}b_1^2\\\sqrt{2}b_1b_2\\b_2^2\end{pmatrix} =a_1^2b_1^2+2a_1b_1a_2b_2+a_2^2b_2^2\\ =(a_1b_1+a_2b_2)^2= \begin{pmatrix}\begin{pmatrix}a_1\\a_2\end{pmatrix}^T\cdot&\begin{pmatrix}b_1\\b_2\end{pmatrix}\end{pmatrix}^2=(\mathbf a^T\cdot\mathbf b)^2 ϕ(a)T⋅ϕ(b)=⎝⎛a122a1a2a22⎠⎞T⋅⎝⎛b122b1b2b22⎠⎞=a12b12+2a1b1a2b2+a22b22=(a1b1+a2b2)2=((a1a2)T⋅(b1b2))2=(aT⋅b)2
这个推导过程表明,转换后向量的点积等于原始向量的点积的平方: ϕ ( a ) T ⋅ ϕ ( b ) = ( a T ⋅ b ) 2 \phi(\mathbf a)^T\cdot\phi(\mathbf b)=(\mathbf a^T\cdot\mathbf b)^2 ϕ(a)T⋅ϕ(b)=(aT⋅b)2
所以,如果将转换映射 φ \varphi φ 应用于所有训练实例,那么对偶公式将包含点积 φ ( x ( i ) ) T ⋅ φ ( x ( j ) ) \varphi(x^{(i)})^T\cdot\varphi(x^{(j)}) φ(x(i))T⋅φ(x(j)) 的计算,从而直接使用 ( x ( i ) T ⋅ x ( j ) ) (x^{(i)^T}\cdot x^{(j)}) (x(i)T⋅x(j)) 来代替转换向量的点积。即不需要转换训练实例,只需要换个计算方式,大大提高了整个过程的计算效率。
在机器学习里,核是能够基于原始向量 a \mathbf a a 和 b \mathbf b b 来计算点积 ϕ ( a ) T ⋅ ϕ ( b ) \phi(\mathbf a)^T\cdot\phi(\mathbf b) ϕ(a)T⋅ϕ(b) 的函数,它不需要计算甚至不需要知道转换函数 φ \varphi φ
常用核函数
- 线性核函数: K ( a , b ) = a T ⋅ b K(\mathbf{a,b})=\mathbf{a^T\cdot b} K(a,b)=aT⋅b
- 多项式核函数: K ( a , b ) = ( γ a T ⋅ b + r ) d K(\mathbf{a,b})=(\gamma\mathbf{a^T\cdot b}+r)^d K(a,b)=(γaT⋅b+r)d ( d 为 多 项 式 的 次 数 ) \quad (d为多项式的次数) (d为多项式的次数)
- 高斯径向基核(RBF)核函数: K ( a , b ) = e x p ( − γ ∣ ∣ a − b ∣ ∣ 2 ) K(\mathbf{a,b})=exp(-\gamma||\mathbf{a-b}||^2) K(a,b)=exp(−γ∣∣a−b∣∣2)
- Sigmoid核函数: K ( a , b ) = t a n h ( γ a T ⋅ b + r ) K(\mathbf{a,b})=tanh(\gamma\mathbf{a^T\cdot b}+r) K(a,b)=tanh(γaT⋅b+r) ( γ > 0 , θ < 0 ) (\quad\gamma >0,\theta <0) (γ>0,θ<0)
问题
1. 支持向量的基本思想是什么?
- 支持向量机的基本思想:拟合类别之间可能的、最宽的间隔。
- 目的是使决策边界之间的间隔最大化,从而分隔出两个类别的训练实例。
- SVM执行软间隔分类时,实际上是在完美分类和你和最宽的间隔之间进行妥协(即允许少数实例落在间隔上)。
- 训练非线性数据集时要使用核函数
2. 什么是支持向量?
- SVM训练完成后,位于间隔上(包括边界上)的实例成为支持向量
- 决策边界完全由支持向量决定,非支持向量对决策边界没有任何影响,由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称为支持向量机。支持向量的个数一般很少,所以支持向量机由很少的"重要的"训练样本确定
- 计算预测结果的时候,只会涉及到支持向量,而不涉及整个训练集
- 在决定分离超平面时只有支持向量起作用,而其他实例点井不起作用。如果移动支持向量将改变所求的解,但是如果在间隔边界以外移动其他实例点,甚去掉这些点,则解是不会改变的。
3. 使用SVM时,对输入值进行缩放为什么重要?
- SVM拟合类别之间可能的、最宽的间隔
- 如果不缩放训练集的输入值,SVM将趋于忽略值较小的特征
- 另外经过特征缩放之后,决策边界可视化会看起来好很多
4. SVM分类器在对实例进行分类时,会输出信心分数么?概率呢?
- SVM能够输出测试实例到决策边界之间的距离,这个可以用作信心分数,但它不能直接转化成类别概率的估算。
- 创建SVM时,在Scikit-Learn中设置probability=True,则训练完成后,算法将使用逻辑回归对SVM分数进行校准(对训练数据额外进行5-折交叉验证的训练),从而得到概率值。这会给SVM添加predict_proba()和predict_log_proba()两种方法。
5. 针对于线性SVM,假设训练集有上千万个实例和几百个特征,你应该使用SVM原始问题还是对偶问题来训练模型?
- 核SVM只能使用对偶问题的形式来训练模型。
- 对于SVM问题来说,原始形式的计算复杂度与训练实例的数量成正比,而其对偶形式的计算复杂度与某个介于 m 2 m^2 m2和 m 3 m^3 m3之间的数量成正比。
所以如果实例数量以百万计,一定要使用原始问题,因为对偶问题在处理实例数较多的训练集会表现得很慢很慢
6. 假设用RBF核训练一个SVM分类器,看起来似乎对训练集你和不足,应该如何调整 γ \gamma γ参数和 C C C参数?
- 拟合不足很可能是由于过度正则化导致的,那么需要提升 γ \gamma γ或者 C C C来降低正则化,从而提升拟合程度。
- γ \gamma γ是一个正则化的超参数,用来表示决策边界的非线性程度的,也就是拟合程度,值越大,非线性越强,拟合程度越高
- C是惩罚项,也就是用在软间隔分类里的控制(保持间隔尽可能最大同时间隔违例最少)平衡的。同样的C越大,拟合程度越高,间隔越大,间隔违例越少。
SMO(Sequential Minimal Optimization)序列最小优化算法
一、算法目标
求出一系列的 α \alpha α 和 b b b,从而计算出 w w w 以确定超平面
二、算法工作原理
每次循环中选择两个 α \alpha α 进行优化处理,增大其中一个,减小另一个
α \alpha α 的选取条件:
- 两个 α \alpha α 必须在间隔边界(也叫决策边界)之外
- 两个 α \alpha α 没有进行过区间化处理或者不在边界上
三、算法代码
# -*-coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import random
class optStruct:
"""
数据结构,维护所有需要操作的值
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
"""
def __init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn #数据矩阵
self.labelMat = classLabels #数据标签
self.C = C #松弛变量
self.tol = toler #容错率
self.m = np.shape(dataMatIn)[0] #数据矩阵行数
self.alphas = np.mat(np.zeros((self.m,1))) #根据矩阵行数初始化alpha参数为0
self.b = 0 #初始化b参数为0
self.eCache = np.mat(np.zeros((self.m,2))) #根据矩阵行数初始化误差缓存,第一列为是否有效的标志位,第二列为实际的误差E的值。
def loadDataSet(fileName):
"""
读取数据
Parameters:
fileName - 文件名
Returns:
dataMat - 数据矩阵
labelMat - 数据标签
"""
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines(): #逐行读取,滤除空格等
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(float(lineArr[2])) #添加标签
return dataMat,labelMat
def calcEk(oS, k):
"""
计算误差Ek
Parameters:
oS - 数据结构
k - 标号为k的数据
Returns:
Ek - 标号为k的数据误差
"""
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T) + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJrand(i, m):
"""
函数说明:随机选择alpha_j的索引值
Parameters:
i - alpha_i的索引值
m - alpha参数个数
Returns:
j - alpha_j的索引值
"""
j = i #选择一个不等于i的j
while (j == i):
j = int(random.uniform(0, m))
return j
def selectJ(i, oS, Ei):
"""
内循环启发方式2,目标是选择合适的第二个alpha值以保证在每次优化中采用最大步长
Parameters:
i - 标号为i的数据的索引值
oS - 数据结构
Ei - 标号为i的数据误差
Returns:
j, maxK - 标号为j或maxK的数据的索引值
Ej - 标号为j的数据误差
"""
maxK = -1; maxDeltaE = 0; Ej = 0 #初始化
oS.eCache[i] = [1,Ei] #根据Ei更新误差缓存
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0] #返回误差不为0的数据的索引值
if (len(validEcacheList)) > 1: #有不为0的误差
for k in validEcacheList: #遍历,找到最大的Ek
if k == i:
continue #不计算i,浪费时间
Ek = calcEk(oS, k) #计算Ek
deltaE = abs(Ei - Ek) #计算|Ei-Ek|
if (deltaE > maxDeltaE): #找到maxDeltaE
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej #返回maxK,Ej
else: #没有不为0的误差
j = selectJrand(i, oS.m) #随机选择alpha_j的索引值
Ej = calcEk(oS, j) #计算Ej
return j, Ej #j,Ej
def updateEk(oS, k):
"""
计算Ek,并更新误差缓存
Parameters:
oS - 数据结构
k - 标号为k的数据的索引值
Returns:
无
"""
Ek = calcEk(oS, k) #计算Ek
oS.eCache[k] = [1,Ek] #更新误差缓存
def clipAlpha(aj,H,L):
"""
修剪alpha_j
Parameters:
aj - alpha_j的值
H - alpha上限
L - alpha下限
Returns:
aj - 修剪后的alpah_j的值
"""
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def innerL(i, oS):
"""
优化的SMO算法
Parameters:
i - 标号为i的数据的索引值
oS - 数据结构
Returns:
1 - 有任意一对alpha值发生变化
0 - 没有任意一对alpha值发生变化或变化太小
"""
# 步骤1:计算误差Ei
Ei = calcEk(oS, i)
# 优化alpha,设定一定的容错率。
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
# 使用内循环启发方式2选择alpha_j,并计算Ej
j,Ej = selectJ(i, oS, Ei)
# 保存更新前的aplpha值,使用深拷贝
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
# 步骤2:计算上下界L和H
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print("L==H")
return 0
# 步骤3:计算eta
eta = 2.0 * oS.X[i,:] * oS.X[j,:].T - oS.X[i,:] * oS.X[i,:].T - oS.X[j,:] * oS.X[j,:].T
if eta >= 0:
print("eta>=0")
return 0
# 步骤4:更新alpha_j
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta
# 步骤5:修剪alpha_j
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
# 更新Ej至误差缓存
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("alpha_j变化太小")
return 0
# 步骤6:更新alpha_i
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
# 更新Ei至误差缓存
updateEk(oS, i)
# 步骤7:更新b_1和b_2
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
# 步骤8:根据b_1和b_2更新b
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else:
return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter):
"""
完整的线性SMO算法
Parameters:
dataMatIn - 数据集矩阵
classLabels - 数据标签
C - 正则化项
toler - 容错率
maxIter - 最大迭代次数
Returns:
oS.b - SMO算法计算的b
oS.alphas - SMO算法计算的alphas
"""
#初始化所有用到的参数
oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler) #初始化数据结构
iter = 0 #初始化当前迭代次数
entireSet = True # entireSet用来选择在哪个内循环进行遍历优化alpha
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): #遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环
alphaPairsChanged = 0
if entireSet: #在数据集上遍历任意可能的alpha
for i in range(oS.m): # 内循环——1,全数据集遍历
alphaPairsChanged += innerL(i,oS) #使用优化的SMO算法来选择第二个alpha,有产生alpha优化返回1,没有产生alpha优化返回0
print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
iter += 1
else: #遍历所有的非边界alpha值,即不在边界0或C上的值
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] #遍历不在边界0和C的alpha,建立非边界alpha值得列表存储在nonBoundIs中
for i in nonBoundIs: # 内循环——2,对刚刚建立好的非边界alpha值表进行遍历
alphaPairsChanged += innerL(i,oS)
print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: #遍历一次后改为非边界遍历
entireSet = False
elif (alphaPairsChanged == 0): #如果遍历完所有非边界数据后alpha没有更新,在进行下一次迭代的时候选择全样本遍历
entireSet = True
print("迭代次数: %d" % iter)
return oS.b,oS.alphas #返回SMO算法计算的b和alphas
def showClassifer(dataMat, classLabels, w, b):
"""
分类结果可视化
Parameters:
dataMat - 数据矩阵
w - 超平面的法向量
b - “截距”
Returns:
None
"""
# 绘制样本点
data_positive = [] # 正样本
data_negative = [] # 负样本
for i in range(len(dataMat)):
if classLabels[i] > 0:
data_positive.append(dataMat[i])
else:
data_negative.append(dataMat[i])
data_positive_np = np.array(data_positive) # 转换为numpy矩阵
data_negative_np = np.array(data_negative) # 转换为numpy矩阵
plt.scatter(np.transpose(data_positive_np)[0], np.transpose(data_positive_np)[1], s=30, alpha=0.7) # 正样本散点图
plt.scatter(np.transpose(data_negative_np)[0], np.transpose(data_negative_np)[1], s=30, alpha=0.7) # 负样本散点图
# 绘制直线
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b - a1 * x1) / a2, (-b - a1 * x2) / a2
plt.plot([x1, x2], [y1, y2])
# 找出支持向量点
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()
def calcWs(alphas,dataArr,classLabels):
"""
计算w
Parameters:
dataArr - 数据矩阵
classLabels - 数据标签
alphas - alphas值
Returns:
w - 计算得到的w
"""
X = np.mat(dataArr); labelMat = np.mat(classLabels).transpose()
m,n = np.shape(X)
w = np.zeros((n,1))
for i in range(m):
w += np.multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
if __name__ == '__main__':
dataArr, classLabels = loadDataSet('testSet.txt')
b, alphas = smoP(dataArr, classLabels, 0.6, 0.001, 40)
w = calcWs(alphas,dataArr, classLabels)
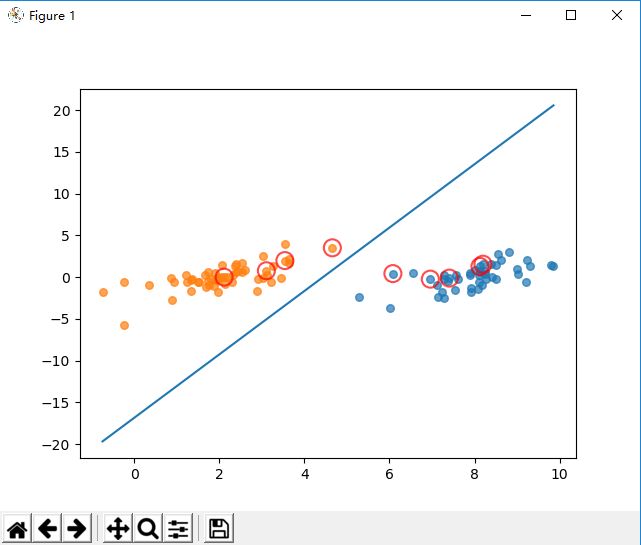
showClassifer(dataArr, classLabels, w, b)
代码运行结果: