Deep Learning-1-一文读懂误差反向传播算法中的关键点、难点
Yolov-1-TX2上用YOLOv3训练自己数据集的流程(VOC2007-TX2-GPU)
Yolov--3--TensorRT中yolov3性能优化加速(基于caffe)
yolov-5-目标检测:YOLOv2算法原理详解
yolov--8--Tensorflow实现YOLO v3
yolov--9--YOLO v3的剪枝优化
yolov--10--目标检测模型的参数评估指标详解、概念解析
yolov--12--YOLOv3的原理深度剖析和关键点讲解
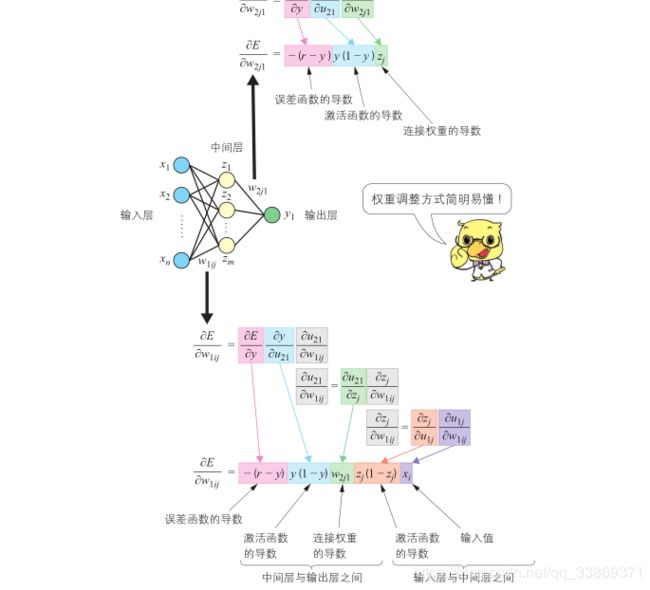
1、梯度下降法中的关键点
https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
http://www.cedar.buffalo.edu/%7Esrihari/CSE574/Chap5/Chap5.3-BackProp.pdf
第一篇博客讲的非常详细,我就不再阐述了,主要写下自己在学习中遇到的问题
重点:
- 如果为多个输出,如上图,误差函数E对W1ij的偏导是对所有输出单元的导数的和
问题一:无限迭代时中间层的误差是否参与?
- 不参与
反向传播算法(Back Propagation)
我们首先直观的介绍反向传播算法,最后再来介绍这个算法的推导。当然读者也可以完全跳过推导部分,因为即使不知道如何推导,也不影响你写出来一个神经网络的训练代码。事实上,现在神经网络成熟的开源实现多如牛毛,除了练手之外,你可能都没有机会需要去写一个神经网络。
我们以监督学习为例来解释反向传播算法。在零基础入门深度学习(2) - 线性单元和梯度下降一文中我们介绍了什么是监督学习,如果忘记了可以再看一下。另外,我们设神经元的激活函数为函数(不同激活函数的计算公式不同,详情见反向传播算法的推导一节)。
我们假设每个训练样本为,其中向量是训练样本的特征,而是样本的目标值。
首先,我们根据上一节介绍的算法,用样本的特征,计算出神经网络中每个隐藏层节点的输出,以及输出层每个节点的输出。
然后,我们按照下面的方法计算出每个节点的误差项:
- 对于输出层节点i,
其中,![]() 是节点的误差项(梯度中的一项,乘上输入值a4就为梯度),
是节点的误差项(梯度中的一项,乘上输入值a4就为梯度),![]() 是节点的输出值,
是节点的输出值,![]() 是样本对应于节点的目标值。举个例子,根据上图,对于输出层节点8来说,它的输出值是
是样本对应于节点的目标值。举个例子,根据上图,对于输出层节点8来说,它的输出值是![]() ,而样本的目标值是
,而样本的目标值是![]() ,带入上面的公式得到节点8的误差项
,带入上面的公式得到节点8的误差项![]() 应该是:
应该是:
![]()
![]()
- 对于隐藏层节点,
其中,![]() 是隐藏层节点的输出值,
是隐藏层节点的输出值,![]() 是输出节点i到它的隐藏层节点k的连接的权重,
是输出节点i到它的隐藏层节点k的连接的权重,![]() 是节点i的下一层节点k的误差项。例如,对于隐藏层节点4来说,计算方法如下:
是节点i的下一层节点k的误差项。例如,对于隐藏层节点4来说,计算方法如下:
最后,更新每个连接上的权值:
其中,![]() 是节点 i 到节点 j 的权重,
是节点 i 到节点 j 的权重,![]() 是一个成为学习速率的常数,
是一个成为学习速率的常数,![]() 是节点 j 的误差项,
是节点 j 的误差项,![]() 是节点 i 传递给节点 j 的输入。例如,权重
是节点 i 传递给节点 j 的输入。例如,权重![]() 的更新方法如下:
的更新方法如下:
类似的,权重 ![]() 的更新方法如下:
的更新方法如下:
偏置项的输入值永远为1。例如,节点4的偏置项应该按照下面的方法计算:
反向传播算法的名字的含义:
显然,计算一个节点的误差项,需要先计算每个与其相连的下一层节点的误差项。这就要求误差项的计算顺序必须是从输出层开始,然后反向依次计算每个隐藏层的误差项,直到与输入层相连的那个隐藏层。
当所有节点的误差项计算完毕后,我们就可以根据式5来更新所有的权重。
流程如下图:
参考:
https://www.zybuluo.com/hanbingtao/note/476663