《深度学习入门:基于Python的理论与实现》学习与总结（二）

接《深度学习入门:基于Python的理论与实现》学习与总结（一）：https://blog.csdn.net/qq_34438969/article/details/88934973

 

（四）神经网络

1、介绍：可自动地从数据中学习到合适的权重参数。

人工神经网络（Artificial Neural Networks，简写为ANNs），简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

 2、激活函数：（一定为非线性函数）

（1）作用：决定如何来激活输入信号的总和。

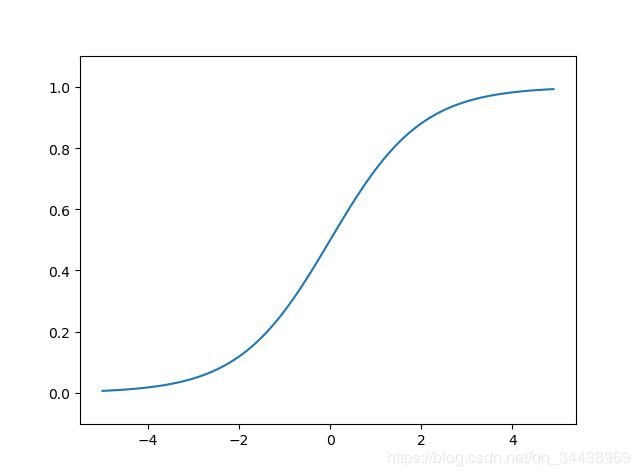
（2）sigmoid 函数与阶跃函数：

① sigmoid 函数：进行信号的转换，转换后信号被转送给下一个神经元。

import numpy as np
import matplotlib.pylab as plt

# sigmoid 函数可支持 NumPy 数组，原因在于 NumPy 数组的广播功能
def sigmoid(x):
    return 1/(1 + np.exp(-x))

# 测试
x = np.arange(-5.0, 5.0, 0.1)   # 以0.1为单位，生成[-5.0, 5.0]范围的数组
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)   # 指定 y 轴的范围
plt.show()

 

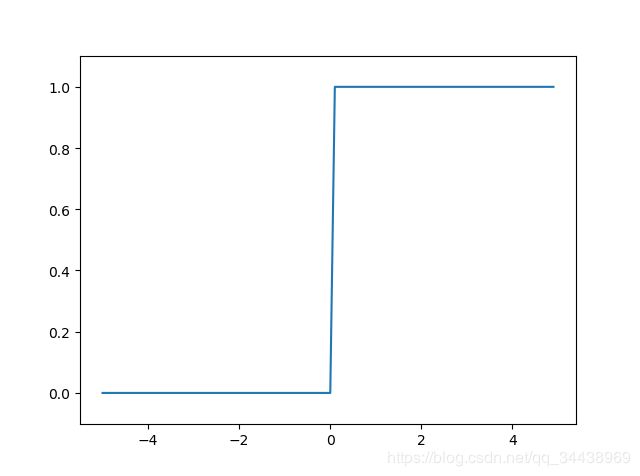
② 阶跃函数：以阈值为界，一旦输入超过阈值，则切换输出。

import numpy as np
import matplotlib.pylab as plt

# 阶跃函数
# def step_function(x):  
#     y = x > 0
#     return y.astype(y, np.int)   # astype()方法通过参数指定期待的类型
def step_function(x):  
    return np.array(x>0, dtype=np.int)

x = np.arange(-5.0, 5.0, 0.1)   # 以0.1为单位，生成[-5.0, 5.0]范围的数组
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)   # 指定 y 轴的范围
plt.show()

# 下图所示，阶跃函数以0为界，输出从0切换为1（或从1切换为0）。其值呈阶梯式变化。

③ 相同点：

A. 形状相似，结构均为 “输入小时，输出接近0（为0）；随着输入增大，输出向1靠近（变成1）”

B. 不管输入信号为何，输出信号的值都在0到1之间

C. 两者均为非线性函数

④ 不同点：

A. “平滑性”：

        sigmoid 函数：一条平滑的曲线，输出随着输入发生连续性的变化。

        阶跃函数：以0为界，输出发生急剧性的变化。

B. 返回值：

        sigmoid 函数：可返回如0.731、0.842……等实数

        阶跃函数：只能返回0或1。

（可推出：感知机中神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号）

 

（3）ReLU （Rectified Linear Unit，修正线性单元）函数

介绍：在输入大于0时，直接输出该值；在输入小于等于0时，输出0。

# 激活函数：ReLU
def relu(x):
    return np.maximum(0, x)   # maximum 函数：从输入的数值中选择较大的那个值进行输出

 

3、多维数组（张量）的运算：

import numpy as np

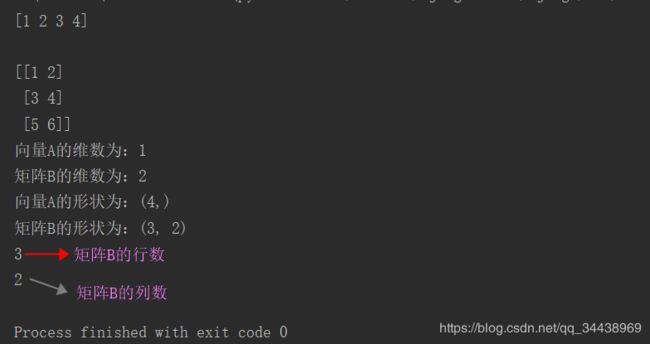
A = np.array([1, 2, 3, 4])   # 一维数组A
B = np.array([[1, 2], [3, 4], [5, 6]])   # 二维数组B（即矩阵B）

print(A)
print()
print(B)
print("向量A的维数为：", end='')
print(np.ndim(A))   # np.ndim()，获取数组的维数（dimension）
print("矩阵B的维数为：", end='')
print(np.ndim(B))

print("向量A的形状为：", end='')
print(A.shape)   # 数组的形状

print("矩阵B的形状为：", end='')
print(B.shape)
print(B.shape[0])   # row，行
print(B.shape[1])   # column，列

 

 

import numpy as np

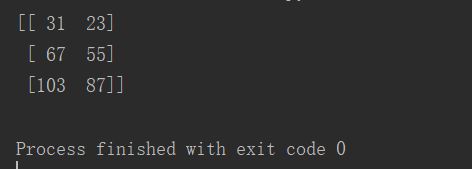
B = np.array([[1, 2], [3, 4], [5, 6]])   # 3 * 2 矩阵B
C = np.array([[5, 9], [13, 7]])   # 2 * 2 矩阵C

print(np.dot(B, C))   # np.dot()函数，计算矩阵B和矩阵C的乘积（点积）

 

4、3层神经网络的实现

import numpy as np

def init_network():   # 进行权重和偏置的初始化，并保存于字典变量network中
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])   # 权重W1
    network['b1'] = np.array([[0.1, 0.2, 0.3]])   # 偏置b1

    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])

    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def sigmoid(x):
    return 1/(1 + np.exp(-x))

def identity_function(x):   # 恒等函数，作出输出层的激活函数
    return x
# 注意：回归问题用恒等函数，分类问题用 softmax 函数

def forward(network, x):   # 封装了将输入信号转换为输出信号的处理过程
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)   # 输入层（第0层）到第1层（隐藏层）的信号传递

    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)   # 第1层到第2层（隐藏层）的信号传递

    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)   # 第2层到输出层（第3层）的信号传递

    return y

network = init_network()
x = np.array([1.0, 5.0])
y = forward(network, x)
print(y)

 5、softmax 函数

# 分类问题：数据属于哪一个类别的问题
# 注意：溢出问题，即表示数值的范围是有限的
'''
softmax 函数，输出解释为概率，其输出是 0.0 到 1.0 之间的实数，输出值的总和为1。
因使用此函数，输出值最大的神经元的位置不变，所以输出层的 softmax 函数一般会被省略
'''
def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y