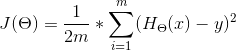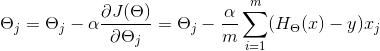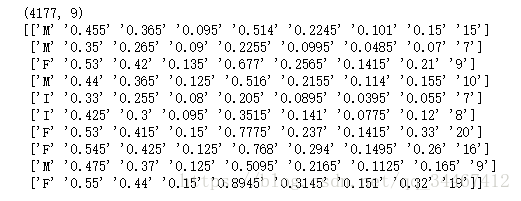吴恩达机器学习，多元线性回归数据实战

最近在学习吴恩达的机器学习课程，觉得讲得有理有据、循序渐进，很多问题豁然开朗，实践是检验真理的唯一标准，为了检验自己的所学所得，也为了更深一步地理解其原理，决定找个数据集来一波实战操作，记录于此一是为了和广大机器学习的学者们分享，其次主要还是记录自己的学习过程，以稳步前行。首次涉及数据实战，代码和思路之中有许多不足之处，还请看官指正。

一、线性回归

线性回归是吴恩达老师的机器学习课程中的第一个入门算法，算法原理简单，容易理解。假设某数据共有m个特征和1个待预测特征y，为了能够通过推测特征y的值，假设与y的函数关系如下：

                                              

函数为线性函数，且具有多个变量，顾称之为多元线性回归，为找到能够尽量贴切地描述与y之间关系的函数，只需确定参数，为了描述预测值与实际值y之间的差异，引进代价函数如下：

                                                 

是关于参数的函数，为使最大程度地接近y，即求使代价函数最小化的变量。

而中参数则由梯度下降算法决定，梯度下降算法通过不断地迭代更新值，使趋于最小化，更新规则为：

                                                    

其中为学习率，若学习率过大可能会使梯度下降算法无法正常工作，若学习率过小则会使梯度下降过慢，增加迭代次数。当随着迭代次数增加，的下降趋于平缓时，梯度下降算法完成，此时的即为所求。

补充：为了使正常地更新，在中添加一个恒为1的特征，即。

 

二、了解数据

在uci网站上找到一个符合要求的数据集Abalone Data Set，数据集链接http://archive.ics.uci.edu/ml/datasets/Abalone。其属性信息如下：

数据集中共包含9个特征，分别是{'性别','壳体最长长度','直径','高度','全重','去壳重量','内脏重量','壳体重量','环数'}，其中性别(Sex)为分类特征，共有M\F\I三种属性，环数(Rings)是我们需要预测的特征，其余特征均为数值属性，我们需要做的工作就是根据样本的前8个特征，猜测其Rings属性值，Let's do it！

 

三、数据预处理

在编写算法之前，先需要对数据进行检查，看数据中有无缺失、是否符合我们所需的规范，实际上这部分的工作是及其麻烦的，好在本数据集已经为我们删除了有缺失值得样本，甚至已经将数据归一化处理，但为了确保算法正常运行，仍需检查数据。

1.读取数据

首先读取数据，查看数据维度，输出数据集前几个样本看是否读取成功。

#读取数据
import numpy as np

abalone_data = np.loadtxt('D:/MachineLearning/鲍鱼/abalone.csv',delimiter=',',dtype='str')
print(abalone_data.shape)
print(abalone_data[:10])

输出如下，可以看出数据读取正常：

2.检查数据

根据数据集的描述，我们需检查一下三点：

①性别属性是否只包含M、F、I三种       

②数据项中是否具有非法字符，即数据中是否有代表缺失值的符号、是否是合法的浮点数     

③根据属性的物理意义，显然这些属性的值都应为大于零的数。

#检查数据
#数据含义：{'性别','壳体最长长度','直径','高度','全重','去壳重量','内脏重量','壳体重量','环数'}

#1.检查性别是否只包含'M','F','I'三种类型
print('Sex Type:',set(abalone_data[:,0]))

#2.检查其余数值项是否包含非法字符
error_number = 0
for rows in abalone_data[:,1:]:
    for sample in rows:
        try:
            float(sample)
        except:
            error_number += 1
            print(rows)
print('Error Number:',error_number)

#3.检查数值项是否符合实际意义
abalone_data_number = abalone_data[:,1:].astype(np.float)
for rows in abalone_data_number>=0.0:
    if False in rows:
        print('rows')

上述代码运行结果如下：

                   

可以确定，①Sex属性中只包括F、M、I三种值，②数据中不存在非法字符，③数据均符合其物理含义。检查数据完毕，接下来就可以使用它们了。

3.整理数据

注意到数据中sex为分类特征，在此将其简单处理，映射成整数项，即M-1，F-2，I-3。此外在上面提到的，为了使正常更新，在x中添加一个恒为1的属性列，最后，将整个数据集按4:1的比例划分为训练集和测试集，当然也可以用其他的方法。

经过运行下面的代码，我们得到了变量x的训练集X_train，预测值y的训练集Y_train，变量x的测试集X_test，预测值y的测试集Y_test。

#整理数据
#1.将sex属性转化为数值项   1-M  2-F  3-I
abalone_sex_col = abalone_data[:,0]
d = {'M':1,'F':2,'I':3}
abalone_sex_col = np.array([[d.get(x)] for x in abalone_sex_col])

#2.获取X
X = np.hstack((abalone_sex_col,abalone_data_number[:,:-1]))
x_0 = [[1]] * X.shape[0]
X = np.hstack((x_0,X))   #为每个样本添加一个恒为1的属性x_0

#3.获取Y
Y = abalone_data_number[:,-1]

#4.获取X和Y训练集测试集
sample_num = int(len(X) * 0.8)
X_train = X[:sample_num]
Y_train = Y[:sample_num]
X_test = X[sample_num:]
Y_test = Y[sample_num:]

四、算法实现

1.训练模型

接下来就简单了，根据原理里面介绍的，首先构建假设函数( 代码中为H(theta,X_row) )，然后构建代价函数（代码中为J（theta）），最后构建每次迭代时的更新函数（代码中为theta_update（alpha,theta_old））。

那么初始的和学习率该如何设置呢，由于梯度下降会不断更新值，且也会被人工调整，那就随机都设置成1好了，首先我们需要确定合适的学习率，在代码中可以这么设置：先运行较小的迭代次数如50次，观察代价函数是否随着迭代过程逐渐减小，选取能使持续减小的最大值，确定值后，适当增加迭代次数，以使梯度下降到最小值。

下面代码中的和迭代次数是多次调整后所得，在代码中绘制了随迭代次数增加的变化过程。此外还将迭代完成后的值输出，以查看函数和数据的拟合情况。

import matplotlib.pyplot as plt
#1.建立假设模型
###输入：theta向量，一个X样本
###输出：预测值
def H(theta,X_row):
    mul = map(lambda x,y:x*y, theta, X_row)
    return sum(mul)

#2.建立代价函数
###输入：theta向量
###输出：代价值
def J(theta):
    dis = 0
    for X_row,y in zip(X_train,Y_train):
        dis += (H(theta,X_row)-y)**2
    return dis/(2*len(X_train))

#3.theta向量更新函数
###输入：学习率alpha,待更新theta向量
###输出：更新后theta向量 
def theta_update(alpha,theta_old):
    theta_new = theta_old.copy()
    for i in range(len(theta_new)):
        temp = 0
        for X_row,y in zip(X_train,Y_train):
            temp += (H(theta_old,X_row) - y) * X_row[i]
        temp /= len(X_train)
        theta_new[i] = theta_old[i] - (alpha*temp)
    return theta_new

#设置初始theta向量
theta_init = [1] * X_train.shape[1]
alpha_init = 0.3
J_list = [J(theta_init)]
for i in range(1500):
    theta_new = theta_update(alpha_init,theta_init)
    J_list.append(J(theta_new))
    theta_init = theta_new
print(J_list[-1])
plt.plot(J_list)
plt.show()

上述代码运行结果如下：

                                      

可以看到在设置学习率为0.3，迭代1500次后得到的使整个训练集的代价函数减小到2.6065，到此，我们可以认为模型训练结束，即可根据此线性模型进行测试了，

2.测试

应用上一步训练得到的模型对测试集进行测试，代码如下：

forecase = []
for x in X_test:
    forecase.append(round(H(theta_init,x)))  #获取测试数据预测值，由于预测的环数为整数，故进行四舍五入处理
confidence_interval = 2  #允许的误差范围
D_value_arr = np.array(forecase) - np.array(Y_test)  #获取预测值与真实值的差值数组
right_num = 0   #正确的个数（在允许误差范围内的个数）
for D_val in D_value_arr:
    if D_val>= -confidence_interval and D_val <= confidence_interval:   #预测值在允许误差范围内
        right_num += 1
print(right_num/(len(forecase)))
      

plt.figure(figsize=(20, 10))
coor_x = [i for i in range(len(forecase))]
plt.scatter(coor_x,D_value_arr)
plt.plot(coor_x,[0]*len(forecase),linewidth=3,color='g')
plt.plot(coor_x,[confidence_interval]*len(forecase),linewidth=3,color='r')
plt.plot(coor_x,[-confidence_interval]*len(forecase),linewidth=3,color='r')
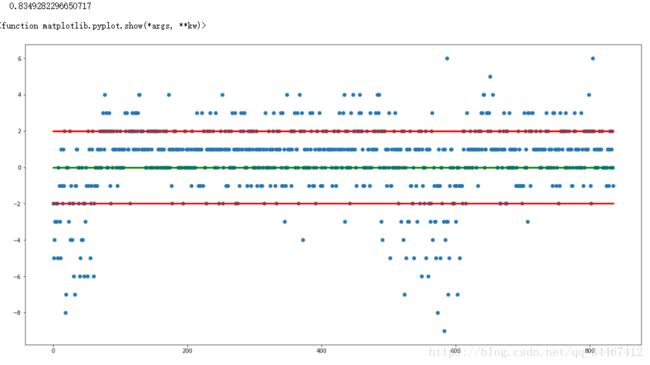
plt.show

运行结果如下：

可以看出在允许的误差范围2以内，其预测准确率达到83.5%，表明训练的模型是可用的。上图是是测试结果图，图中蓝点纵坐标表示预测值与真实值之差，横坐标为样本编号，绿色横线为Y=0的水平线，在该线上的点表示预测完全准确，遗憾的是允许误差为0的准确率仅为20.93%，上下红色横线之间代表在允许误差内预测正确的点，从该图中可以看出在数据集前端和中部有部分数据测试异常偏离，这或许可以成为该模型的改进点。

本次实战到此暂告一段落，初次撰写博文，也是初次涉及机器学习实战，必定有诸多不足甚至错误之处，还望看官指正。