python数据分析之数据离散化——等宽&等频&聚类离散
数据离散化的意义
数据离散化是指将连续的数据进行分段,使其变为一段段离散化的区间。分段的原则有基于等距离、等频率或优化的方法。
离散化的原因
1.模型限制
比如决策树、朴素贝叶斯等算法,都是基于离散型的数据展开的。如果要使用该类算法,必须将离散型的数据进行。有效的离散化能减小算法的时间和空间开销,提高系统对样本的分类聚类能力和抗噪声能力。
2. 离散化的特征更易理解
比如工资收入,月薪2000和月薪20000,从连续型特征来看高低薪的差异还要通过数值层面才能理解,但将其转换为离散型数据(底薪、高薪),则可以更加直观的表达出了我们心中所想的高薪和底薪。
3. 使模型结果更加稳定
比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问,如果按区间离散化,划分区间是非常关键的。
4. 调高计算效率
离散特征的增加和减少都很容易,易于模型的快速迭代。(离散特征的增加和减少,模型也不需要调整,重新训练是必须的,相比贝叶斯推断方法或者树模型方法迭代快)。稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展。
5. 图像处理中的二值化处理
将256个亮度等级的灰度图像通过适当的阈值选取而获得仍然可以反映图像整体和局部特征的二值化图像。这样有利于图像的进一步处理,使图像变得简单,而且数据量减小,能凸显出感兴趣的目标的轮廓。
连续数据离散化方法
- 等宽离散法:等距区间或自定义区间进行离散,有点是灵活,保持原有数据分布
- 等频离散法:根据数据的频率分布进行排序,然后按照频率进行离散,好处是数据变为均匀分布,但是会更改原有的数据结构
- 聚类离散法:使用k-means将样本进行离散处理
- 分位数法:使用四分位、五分位、十分位等进行离散
- 卡方:通过使用基于卡方的离散方法,找出数据的最佳临近区间并合并,形成较大的区间
- 二值化:数据跟阈值比较,大于阈值设置为某一固定值(例如1),小于设置为另一值(例如0),然后得到一个只拥有两个值域的二值化数据集。
注意: 卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。
具体讲解
1. 等宽法
将属性的值域从最小值到最大值分成具有相同宽度的n个区间,n由数据特点决定,往往是需要有业务经验的人进行评估。比如属性值在[0,60]之间,最小值为0,最大值为60,我们要将其分为3等分,则区间被划分为[0,20] 、[21,40] 、[41,60],每个属性值对应属于它的那个区间。
我们随机产生200个人的年龄数据,然后通过等宽离散化,并进行可视化。这里主要使用的是pandas库中的cut函数。其定义如下:
cut(x, bins, right=True, labels=None, retbins=False, precision=3,
include_lowest=False)
【案例代码】
可视化部分代码
# 可视化
def cluster_plot(d, k):
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12, 4))
for j in range(0, k):
plt.plot(data[d == j], [j for i in d[d == j]], 'o')
plt.ylim(-0.5, k - 0.5)
return plt
等宽离散化代码
data = np.random.randint(1, 100, 200)
k = 5 # 分为5个等宽区间
# 等宽离散
d1 = pd.cut(data, k, labels=range(k))
cluster_plot(d1, k).show()
data = np.random.randint(1, 100, 200)
k = 6
bins = [0, 10, 18, 30, 60, 100] # 自定义区间
d2 = pd.cut(data, bins=bins, labels=range(k-1))
cluster_plot(d2, k).show()
2.等频法
等频法是将相同数量的记录放在每个区间,保证每个区间的数量基本一致。即将属性值分为具有相同宽度的区间,区间的个数k根据实际情况来决定。比如有60个样本,我们要将其分为k=3部分,则每部分的长度为20个样本。
我们随机产生200个人的年龄数据,然后通过等宽离散化,并进行可视化。这里主要使用的是pandas库中的qcut函数。其缺点是边界易出现重复值,如果为了删除重复值可以设置 duplicates=‘drop’,但易出现于分片个数少于指定个数的问题。其函数定义如下:
qcut(x, q, labels=None, retbins=False, precision=3, duplicates='raise')
【案例代码】
data = np.random.randint(1, 100, 200)
k = 6
d3=pd.qcut(data,k)
print(d3.value_counts())
【效果】
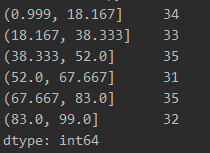
根据上面可以看出,每个区间数量大致相同,但是区间位置的意义却不清楚。
【自己实现的等频离散化】
data = np.random.randint(1, 100, 200)
data = pd.Series(data)
k = 6
# 等频率离散化
w = [1.0 * i / k for i in range(k + 1)]
w = data.describe(percentiles=w)[4:4 + k + 1]
w[0] = w[0] * (1 - 1e-10)
d4 = pd.cut(data, w, labels=range(k))
cluster_plot(d4, k).show()
3.基于聚类
一维聚类离散包括两个过程:选取聚类算法(K-Means算法)将连续属性值进行聚类;处理聚类之后的到的k个簇,得到每个簇对应的分类值(类似这个簇的标记),将在同一个簇内的属性值做为统一标记。
【案例代码】
# 聚类离散
from sklearn.cluster import KMeans
data = np.random.randint(1, 100, 200)
data = pd.Series(data)
k=5
kmodel = KMeans(n_clusters=k)
kmodel.fit(data.reshape((len(data), 1)))
c = pd.DataFrame(kmodel.cluster_centers_, columns=list('a')).sort_values(by='a')
# rolling_mean表示移动平均,即用当前值和前2个数值取平均数,
# 由于通过移动平均,会使得第一个数变为空值,因此需要使用.iloc[1:]过滤掉空值。
w = pd.rolling_mean(c, 2).iloc[1:]
w = [0] + list(w['a']) + [data.max()]
d5 = pd.cut(data, w, labels=range(k))
cluster_plot(d5, k).show()
总结
由等宽离散结果我们可以直观的看出等宽离散的缺点,其缺点在于对噪点过于敏感,倾向于不均匀的把属性值分布到各个区间,导致有些区间的数值极多,而有些区间极少,严重损坏离散化之后建立的数据模型。等频离散不会像等宽离散一样,出现某些区间极多或者极少的情况。但是根据等频离散的原理,为了保证每个区间的数据一致,很有可能将原本是相同的两个数值却被分进了不同的区间,这对最终模型的损坏程度一点都不亚于等宽离散。聚类离散当然好,但是前提是依据聚类,聚类的好坏很影响离散化,还是需要经验决定。



