大川教你彻底理解拉格朗日插值
本文部分转载自:
知乎
中文维基
有何用
板子:给出平面上n+1个点,求一条穿过这n+1个点的n次多项式,或这个多项式在另一个点处的值。
显然可以高斯消元求出每一项系数,然后输出/直接爆算。
其实拉格朗日插值有两种:朴素的,和重心拉个朗日插值。一般情况下,朴素的和高斯消元在求解第1问时复杂度没有区别,但是后者无论第几问都可以用 O ( n 2 ) O(n^2) O(n2)的复杂度爆艹高斯消元 O ( n 3 ) O(n^3) O(n3)。
以下全都介绍求多项式的方法。
直观理解
这里的是朴素插值。
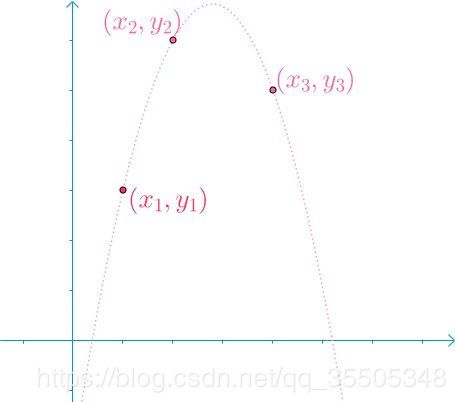
比如说,已知下面这几个点,我想找到一根穿过它们的曲线:
首先显然可以用一个n次多项式经过,不保证第n项系数是否为0。
然后高斯消元告诉我们,这应该是一个二次曲线。
y = a 0 + a 1 x + a 2 x 2 y=a_0+a_1x+a_2x^2 y=a0+a1x+a2x2
然后,显然可以解方程。
{ y 1 = a 0 + a 1 x 1 1 + a 2 x 1 2 y 2 = a 0 + a 1 x 2 1 + a 2 x 2 2 y 3 = a 0 + a 1 x 3 1 + a 2 x 3 2 \begin{cases} y_1=a_0+a_1x_1^1+a_2x_1^2 \\ y_2=a_0+a_1x_2^1+a_2x_2^2 \\ y_3=a_0+a_1x_3^1+a_2x_3^2 \end{cases} ⎩⎪⎨⎪⎧y1=a0+a1x11+a2x12y2=a0+a1x21+a2x22y3=a0+a1x31+a2x32
然而,如果不解方程呢?
拉格朗日发现,我们可以用三根二次函数相加得到我们要的函数。
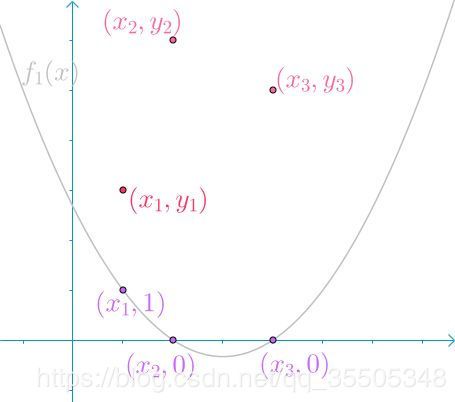
第一个函数 f 1 ( x ) f_1(x) f1(x),在 x = x 1 x=x_1 x=x1处值为1,在 x = x 2 , x 3 x=x_2,x_3 x=x2,x3处都为0。
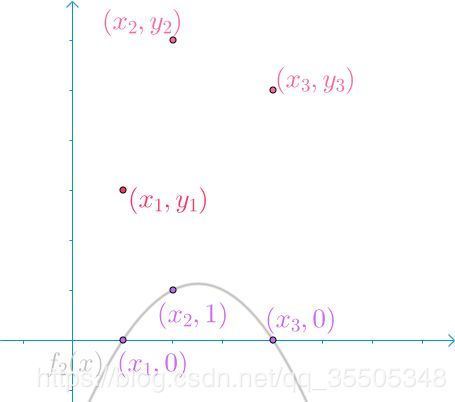
第二个函数 f 2 ( x ) f_2(x) f2(x),在 x = x 2 x=x_2 x=x2处值为1,其余两处值为0。
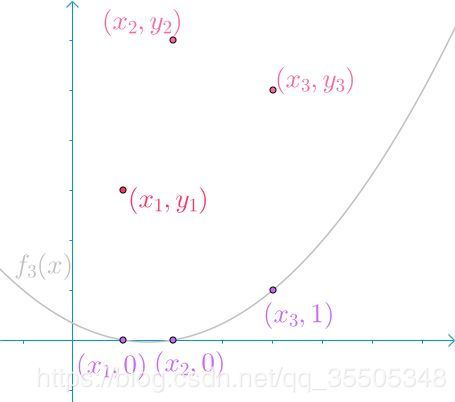
第三个函数 f 3 ( x ) f_3(x) f3(x),在 x = x 3 x=x_3 x=x3处值为1,其余两处值为0。
现在我们考察 y 1 f 1 ( x ) + y 2 f 2 ( x ) + y 3 f 3 ( x ) y_1f_1(x)+y_2f_2(x)+y_3f_3(x) y1f1(x)+y2f2(x)+y3f3(x)的性质。首先,它是一个二次函数。然后,它过这三个点。高斯消元告诉我们,这个函数就是唯一的二次函数 which(经过这三个点)。
形式化的表述
首先还是朴素插值。
假如有 n + 1 n+1 n+1个点,每个点形如 ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . (x_0,y_0),(x_1,y_1),(x_2,y_2),... (x0,y0),(x1,y1),(x2,y2),...,假设任意两个x都不相同,那么最后得到的多项式肯定是:
L ( x ) = ∑ j = 0 n ( y i ∏ i = 0 , i ≠ j n x − x i x j − x i ) L(x)=\sum_{j=0}^n(y_i\prod_{i=0,i\neq j}^n \frac{x-x_i}{x_j-x_i}) L(x)=j=0∑n(yii=0,i̸=j∏nxj−xix−xi)
显然,这个式子计算连乘部分是n^2的(直接二项打开),总复杂度 O ( n 3 ) O(n^3) O(n3)。
而且,如果在原点集的基础上加一个点,它需要比较大的复杂度取更新。
以上是傻逼做法。
正常的做法应该是,发现每一个连乘的分子乘上一个二项式能变成一个统一的多项式,所以处理的时候直接用不需要的那个二项式去除那个多项式就行(下面的常数计算)。1
为了方便增加一个点的改进(正常做法)
令拉格朗日基本多项式
l j ( x ) = ∏ i = 0 , i ≠ j n x − x i x j − x i l_j(x)=\prod_{i=0,i\neq j}^n \frac{x-x_i}{x_j-x_i} lj(x)=i=0,i̸=j∏nxj−xix−xi
再令
l ( x ) = ∏ i = 0 n x − x i l(x)=\prod_{i=0}^n x-x_i l(x)=i=0∏nx−xi
可以得到
l j ( x ) = l ( x ) x − x j 1 ∏ i = 0 , i ≠ j n ( x j − x i ) l_j(x)=\frac{l(x)}{x-x_j} \frac{1}{\prod_{i=0,i\neq j}^n(x_j-x_i)} lj(x)=x−xjl(x)∏i=0,i̸=jn(xj−xi)1
令重心权 w j w_j wj为
w j = ∏ i = 0 , i ≠ j n ( x j − x i ) w_j=\prod_{i=0,i\neq j}^n(x_j-x_i) wj=i=0,i̸=j∏n(xj−xi)
就有
l j ( x ) = l ( x ) w j x − x j l_j(x)=l(x) \frac{w_j}{x-x_j} lj(x)=l(x)x−xjwj
于是最后的多项式就是
L ( x ) = l ( x ) ∑ j = 0 n w j x − x j y j L(x)=l(x)\sum_{j=0}^n \frac{w_j}{x-x_j} y_j L(x)=l(x)j=0∑nx−xjwjyj
对于这个公式,我们可以每次插入一个点,插一个点On,又因为除的项只有两项,可以手动讨论,因此最后统计n^2,显然求出答案是 O ( n 2 ) O(n^2) O(n2)的。
只要求值
前面说过,如果只是求值,那么朴素的拉格朗日插值也能做到 O ( n 2 ) O(n^2) O(n2)。就是直接把要求的x带入上面一堆式子中的x即可。
以上四行为第一次更新所更新的内容。初读可以忽略。 ↩︎