PyTorch 深度学习实战（12）：Actor-Critic 算法与策略优化

在上一篇文章中，我们介绍了强化学习的基本概念，并使用深度 Q 网络（DQN）解决了 CartPole 问题。本文将深入探讨 Actor-Critic 算法，这是一种结合了策略梯度（Policy Gradient）和值函数（Value Function）的强化学习方法。我们将使用 PyTorch 实现 Actor-Critic 算法，并应用于经典的 CartPole 问题。

---

一、Actor-Critic 算法基础

Actor-Critic 算法是强化学习中的一种重要方法，它结合了策略梯度方法和值函数方法的优点。其核心思想是通过两个网络分别学习策略（Actor）和值函数（Critic），从而更高效地进行策略优化。

1. Actor-Critic 的核心组件

• Actor（策略网络）：

  • 负责学习策略，即在给定状态下选择动作的概率分布。

  • 目标是最大化累积奖励。

  • 通过策略梯度方法更新参数。

• Critic（值函数网络）：

  • 负责评估状态或状态-动作对的价值。

  • 目标是准确估计当前策略的价值函数。

  • 通过时序差分（Temporal Difference, TD）误差更新参数。

2. 优势与特点

• 降低方差：

  • 通过 Critic 提供的值函数估计，Actor-Critic 算法可以减少策略梯度方法的高方差问题。

• 更稳定的训练：

  • Critic 提供了更准确的反馈信号，使得策略优化更加稳定。

• 适用范围广：

  • 可以应用于连续动作空间和离散动作空间的问题。

3. 算法流程

1. Actor 根据当前策略选择动作。

2. 环境执行动作，返回奖励和下一状态。

3. Critic 计算当前状态的价值和 TD 误差。

4. 使用 TD 误差更新 Actor 和 Critic 的参数。

5. 重复上述过程，直到策略收敛。

---

二、CartPole 问题实战

我们将使用 PyTorch 实现 Actor-Critic 算法，并应用于 CartPole 问题。目标是控制小车使其上的杆子保持直立。

1. 问题描述

CartPole 环境的状态空间包括小车的位置、速度、杆子的角度和角速度。动作空间包括向左或向右移动小车。智能体每保持杆子直立一步，就会获得 +1 的奖励，当杆子倾斜超过一定角度或小车移动超出范围时，游戏结束。

2. 实现步骤

1. 安装并导入必要的库。

2. 定义 Actor 和 Critic 网络。

3. 定义经验回放缓冲区。

4. 定义 Actor-Critic 训练过程。

5. 测试模型并评估性能。

3. 代码实现

以下是完整的代码实现：

import gym
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
from torch.optim.lr_scheduler import CosineAnnealingLR
​
# 设置 Matplotlib 支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
​
env = gym.make('CartPole-v1')
​
# 固定随机种子
env.seed(42)
torch.manual_seed(42)
np.random.seed(42)
random.seed(42)
​
class Actor(nn.Module):
    def __init__(self, state_size, action_size):
        super(Actor, self).__init__()
        self.fc1 = nn.Linear(state_size, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, action_size)
        self.init_weights()
​
    def init_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                if m == self.fc3:
                    nn.init.xavier_normal_(m.weight, gain=0.01)
                else:
                    nn.init.xavier_uniform_(m.weight)
                nn.init.constant_(m.bias, 0.0)
​
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        logits = self.fc3(x)
        return logits
​
class Critic(nn.Module):
    def __init__(self, state_size):
        super(Critic, self).__init__()
        self.fc1 = nn.Linear(state_size, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, 1)
        self.init_weights()
​
    def init_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                nn.init.xavier_uniform_(m.weight)
                nn.init.constant_(m.bias, 0.0)
​
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x
​
class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = deque(maxlen=capacity)
​
    def push(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))
​
    def sample(self, batch_size):
        state, action, reward, next_state, done = zip(*random.sample(self.buffer, batch_size))
        return np.array(state), np.array(action), np.array(reward), np.array(next_state), np.array(done)
​
    def __len__(self):
        return len(self.buffer)
​
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
actor = Actor(state_size, action_size)
​
class TwinCritic(nn.Module):
    def __init__(self, state_size):
        super().__init__()
        self.critic1 = Critic(state_size)
        self.critic2 = Critic(state_size)
​
    def forward(self, x):
        return self.critic1(x), self.critic2(x)
​
# 初始化网络
critic = TwinCritic(state_size)
target_critic = TwinCritic(state_size)
target_critic.load_state_dict(critic.state_dict())
​
actor_optimizer = optim.Adam(actor.parameters(), lr=0.0005)
critic_optimizer = optim.Adam(critic.parameters(), lr=0.0005)
actor_scheduler = CosineAnnealingLR(actor_optimizer, T_max=500, eta_min=1e-5)
critic_scheduler = CosineAnnealingLR(critic_optimizer, T_max=500, eta_min=1e-5)
buffer = ReplayBuffer(10000)
​
batch_size = 128 
while len(buffer) < batch_size:
    state = env.reset()
    done = False
    while not done:
        action = env.action_space.sample()
        next_state, reward, done, _ = env.step(action)
        buffer.push(state, action, reward, next_state, done)
        state = next_state
​
def train(actor, critic, target_critic, buffer, batch_size, gamma=0.99):
    if len(buffer) < batch_size:
        return    
​
    state, action, reward, next_state, done = buffer.sample(batch_size)
    state = torch.FloatTensor(state)
    next_state = torch.FloatTensor(next_state)
    action = torch.LongTensor(action)
    reward = torch.FloatTensor(reward)
    done = torch.FloatTensor(done)
​
    # Critic 更新
    value1, value2 = critic(state)
    next_value1, next_value2 = target_critic(next_state)
    next_value = torch.min(next_value1, next_value2).detach()
    target_value = reward + gamma * next_value * (1 - done)
    critic_loss = F.mse_loss(value1, target_value) + F.mse_loss(value2, target_value)
​
    critic_optimizer.zero_grad()
    critic_loss.backward()
    torch.nn.utils.clip_grad_norm_(critic.parameters(), max_norm=1.0)
    critic_optimizer.step()
​
    # Actor 更新
    logits = actor(state)
    probs = F.softmax(logits, dim=-1)
    log_probs = F.log_softmax(logits, dim=-1)
    entropy = -(probs * log_probs).sum(dim=-1).mean()
    log_prob = log_probs.gather(1, action.unsqueeze(1)).squeeze(1)
    advantage = target_value - 0.5 * (value1.detach() + value2.detach())  # 平均优势
    actor_loss = (-log_prob * advantage).mean() - 0.1 * entropy
​
    actor_optimizer.zero_grad()
    actor_loss.backward()
    torch.nn.utils.clip_grad_norm_(actor.parameters(), max_norm=5.0)
    actor_optimizer.step()
​
    actor_scheduler.step()
    critic_scheduler.step()
​
    # 更新目标网络
    for target_param, param in zip(target_critic.parameters(), critic.parameters()):
        target_param.data.copy_(0.95 * target_param.data + 0.05 * param.data)
​
def test(env, actor, episodes=10):
    total_reward = 0
    for _ in range(episodes):
        state = env.reset()
        done = False
        while not done:
            state_tensor = torch.FloatTensor(state).unsqueeze(0)
            logits = actor(state_tensor)
            probs = F.softmax(logits, dim=-1)
            action = torch.multinomial(probs, 1).item()
            next_state, reward, done, _ = env.step(action)
            total_reward += reward
            state = next_state
    return total_reward / episodes
​
episodes = 1000
batch_size = 64
gamma = 0.99
rewards = []
​
for episode in range(episodes):
    state = env.reset()
    done = False
    total_reward = 0
​
    while not done:
        state_tensor = torch.FloatTensor(state).unsqueeze(0)
        logits = actor(state_tensor)
        probs = F.softmax(logits, dim=-1)
        action = torch.multinomial(probs, 1).item()
        next_state, reward, done, _ = env.step(action)
        buffer.push(state, action, reward, next_state, done)
        state = next_state
        total_reward += reward
​
        if len(buffer) >= batch_size:
            train(actor, critic, target_critic, buffer, batch_size, gamma)
​
    rewards.append(total_reward)
​
    if (episode + 1) % 50 == 0:
        avg_reward = test(env, actor)
        print(f"Episode: {episode + 1}, Avg Reward: {avg_reward:.2f}")
​
plt.plot(rewards)
plt.xlabel("Episode")
plt.ylabel("Total Reward")
plt.title("Actor-Critic train")
plt.show()

---

三、代码解析

1. Actor 和 Critic 网络：

   • Actor 网络输出动作的 logits（未归一化的概率），通过 F.softmax 转换为概率分布。

   • Critic 网络输出状态的价值估计。

2. 经验回放缓冲区：

   • 使用 deque 实现经验回放缓冲区，存储状态、动作、奖励等信息。

3. 训练过程：

   • 使用 Critic 计算 TD 误差，更新 Critic 网络。

   • 使用 TD 误差作为优势函数，更新 Actor 网络。

   • 使用梯度裁剪（gradient clipping）防止梯度爆炸。

4. 测试过程：

   • 在测试环境中评估模型性能，计算平均奖励。

5. 可视化：

   • 绘制训练过程中的总奖励曲线。

---

四、运行结果

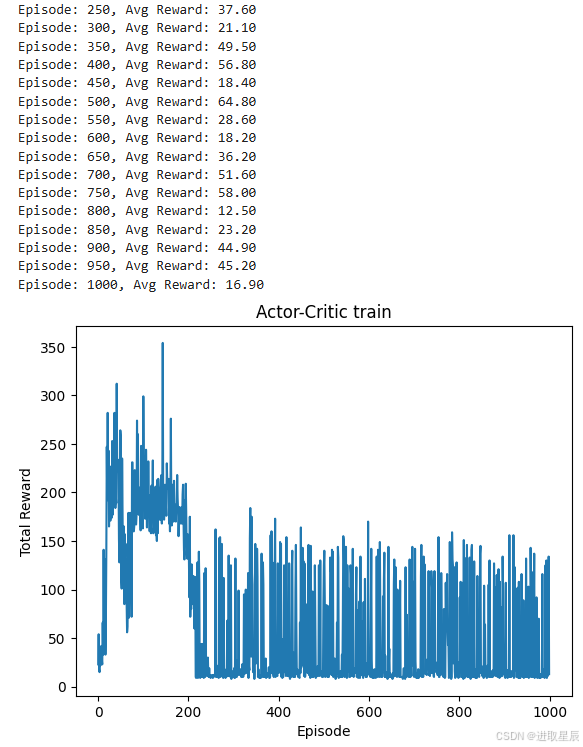
运行上述代码后，你将看到以下输出：

• 训练过程中每 50 个 episode 打印一次平均奖励。

• 训练结束后，绘制训练过程中的总奖励曲线。

---

五、总结

本文介绍了 Actor-Critic 算法的基本原理，并使用 PyTorch 实现了一个简单的 Actor-Critic 模型来解决 CartPole 问题。通过这个例子，我们学习了如何结合策略梯度和值函数方法进行强化学习。

在下一篇文章中，我们将探讨更高级的强化学习算法，如 Proximal Policy Optimization (PPO) 和 Deep Deterministic Policy Gradient (DDPG)。敬请期待！

代码实例说明：

• 本文代码可以直接在 Jupyter Notebook 或 Python 脚本中运行。

• 如果你有 GPU，可以将模型和数据移动到 GPU 上运行，例如：actor = actor.to('cuda')，state = state.to('cuda')。

希望这篇文章能帮助你更好地理解 Actor-Critic 算法！如果有任何问题，欢迎在评论区留言讨论。