树状数组的一些理解
树状数组中的 l o w b i t lowbit lowbit的一些具体意思,有一点感悟。
原理:这个百度上都有,就不说了。
假设树状数组为 c [ ] c[] c[],原数组为 a [ ] a[] a[], 1 − i 1-i 1−i的和数组为 s u m [ i ] sum[i] sum[i]。
则经过观察有:
c [ i ] = a [ i − 2 k + 1 ] + a [ i − 2 k + 2 ] + . . . + a [ i ] c[i]=a[i-2^{k}+1]+a[i-2^{k}+2]+...+a[i] c[i]=a[i−2k+1]+a[i−2k+2]+...+a[i]
s u m [ i ] = c [ i ] + c [ i − 2 k 1 ] + c [ i − 2 k 1 − 2 k 2 ] + . . . + c [ 0 ] sum[i]=c[i]+c[i-2^{k1}]+c[i-2^{k1}-2^{k2}]+...+c[0] sum[i]=c[i]+c[i−2k1]+c[i−2k1−2k2]+...+c[0]
这里的 l o w b i t ( x ) lowbit(x) lowbit(x)有两种求法:
l o w b i t ( x ) = ( x ) a n d ( − x ) lowbit(x)=(x )and( -x) lowbit(x)=(x)and(−x)
l o w b i t ( x ) = ( x ) x o r ( x − 1 ) lowbit(x)=(x)xor(x-1) lowbit(x)=(x)xor(x−1)
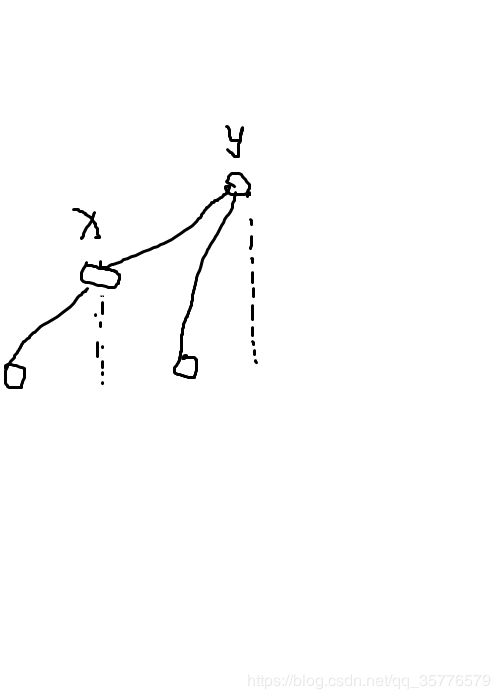
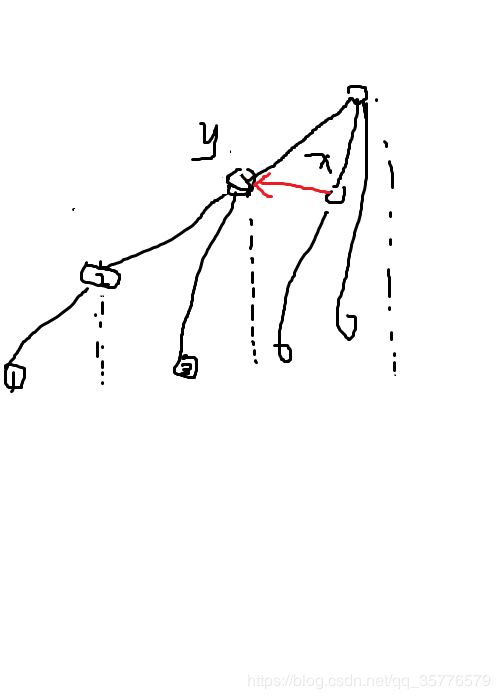
y = x + l o w b i t ( x ) y=x+lowbit(x) y=x+lowbit(x):此时的 y y y,在树状数组的图形中,就是 x x x的父亲节点,也就是 y y y包括 x x x的覆盖范围。
y = x − l o w b i t ( x ) y=x-lowbit(x) y=x−lowbit(x):此时的 y y y,在树状数组的图形中就是一个相邻的节点。
树状数组可以支持:
1.单点修改,区间查询
2.区间修改,单点查询
3.区间修改,区间查询
4.区间最值
5.二维树状数组
1.单点修改,区间查询:
树状数组的元素代表对应区间 a [ i ] a[i] a[i]的和,可能需要离散化。
2.区间修改,单点查询:
这个需要转化到差分的形式,树状数组的每个元素维护对应区间 a [ i ] − a [ i − 1 ] a[i]-a[i-1] a[i]−a[i−1]的值。
3.区间修改,区间查询:
这个就需要推导一下了。
首先,令 d [ i ] = a [ i ] − a [ i − 1 ] d[i]=a[i]-a[i-1] d[i]=a[i]−a[i−1]
∑ i = 1 n a [ i ] = ∑ k = 1 n ( ∑ i = 1 k d [ i ] + a [ 0 ] ) , a [ 0 ] = 0 \sum_{i=1}^n a[i]=\sum_{k=1}^n(\sum_{i=1}^k d[i] +a[0]),a[0]=0 ∑i=1na[i]=∑k=1n(∑i=1kd[i]+a[0]),a[0]=0
化简后为:
∑ i = 1 n a [ i ] = ∑ k = 1 n ( n − i + 1 ) ∗ d [ i ] = ( n + 1 ) ∗ ∑ i = 1 n d [ i ] − ∑ i = 1 n i ∗ d [ i ] \sum_{i=1}^na[i]\\ =\sum_{k=1}^n (n-i+1)*d[i]\\ =(n+1)*\sum_{i=1}^nd[i]-\sum_{i=1}^ni*d[i] ∑i=1na[i]=∑k=1n(n−i+1)∗d[i]=(n+1)∗∑i=1nd[i]−∑i=1ni∗d[i]
因此,维护一下 d [ i ] d[i] d[i]和 i ∗ d [ i ] i*d[i] i∗d[i]就可以了。
4.区间最值:
(HDU 1754)
这里可以考虑附上核心代码:
void update(int pos){
while(pos<=N){
t[pos]=a[pos];
int y=lowbit(pos);
for(int i=0;(1<<i)<y;++i) t[pos]=max(t[pos],t[pos-(1<<i)]);
pos+=y;
}
}
int query(int l,int r){
int ans=0;
//cout<
while(l<=r){
//cout<
if(r-lowbit(r)+1>=l) ans=max(ans,t[r]),r-=lowbit(r);
else ans=max(ans,a[r]),--r;
}
return ans;
}
解释一下核心部分,这里有两个数组 a [ ] a[] a[]表示数组中的值, t [ ] t[] t[]表示树状数组中对应的区间的最大值。
对于 u p d a t e update update中的一段:
for(int i=0;(1<<i)<y;++i) t[pos]=max(t[pos],t[pos-(1<<i)]);
这里是在枚举树状数组中某个节点的所有子节点,想象一下,这些节点 p o s − ( 1 < < i ) pos-(1<
对于 q u e r y query query中的一段:
if(r-lowbit(r)+1>=l) ans=max(ans,t[r]),r-=lowbit(r);
else ans=max(ans,a[r]),--r;
这里主要是在考虑该节点能不能完全包含在区间内,如果能就比较答案与这段区间的值,如果不能,就一个一个的枚举。
5.二维树状数组
对于 x x x的每个节点,再开一个树状数组来进行记录 y y y的信息。
可以用树套树等代替。
统计的是一个正方形方块内的和。 ( 1 − n , 1 − m ) (1-n,1-m) (1−n,1−m)
附上代码:
struct Tree_array{
LL t[maxn];
void init(){ memset(t,0,sizeof t); }
void update(int pos,int num){
while(pos<=N){
t[pos]+=num;
pos+=lowbit(pos);
}
}
LL query(int pos){
LL sum=0;
while(pos){
sum+=t[pos];
pos-=lowbit(pos);
}
return sum;
}
}T[maxn];
void update(int x,int y,int z){
while(x<=N){
T[x].update(y,z);
x+=lowbit(x);
}
}
LL query(int x,int y){
LL sum=0;
while(x){
sum+=T[x].query(y);
x-=lowbit(x);
}
return sum;
}