代换密码解密
请解密以下代换密码的密文:
JGRMQOYGHMVBJWRWQFPWHGFFDQGFPFZRKBEEBJIZQQOCIBZKLFAFGQVFZFWWE
OGWOPFGFHWOLPHLRLOLFDMFGQWBLWBWQOLKFWBYLBLYLFSFLJGRMQBOLWJVFP
FWQVHQWFFPQOQVFPQOCFPOGFWFJIGFQVHLHLROQVFGWJVFPFOLFHGQVQVFILE
OGQILHQFQGIQVVOSFAFGBWQVHQWIJVWJVFPFWHGFIWIHZZRQGBABHZQOCGFHX
首先我们要知道代换密码的定义,代换密码就是使用substitution来进行加密的算法。通过查询资料,知道攻击方法主要有:
①穷举法:在密钥空间较小的情况下,采用暴力破解方式攻击方法。
②频率统计:在密文长度足够长的时候,可使用词频分析。
③爬山法:选择性地尝试不同解密密钥,然后给每一个解密出来的明文标记上一个适应度。若解密出来的明文越接近我们的日常用的英语,它的适应度就越高;若解密出来的明文越难读懂或者越不像我们日常用的英语,则其适应度越低。
本来我已经选择用频率分析的方法去做,然后得出未解密的字母频率为:
[('F', 37), ('Q', 26), ('W', 21), ('G', 19), ('L', 17), ('O', 16), ('V', 15), ('H', 14), ('B', 12), ('P', 10), ('I', 9), ('J', 9), ('R', 7), ('Z', 7), ('M', 4), ('E', 4), ('C', 3), ('K', 3), ('A', 3), ('Y', 3), ('D', 2), ('S', 2), ('X', 1)]
解密后的字母频率为:[('E', 37), ('T', 26), ('S', 21), ('R', 19), ('N', 17), ('O', 16), ('H', 15), ('A', 14), ('I', 12), ('M', 10), ('C', 9), ('U', 9), ('Y', 7), ('L', 7), ('P', 4), ('F', 4), ('G', 3), ('B', 3), ('D', 3), ('V', 3), ('X', 2), ('W', 2), ('K', 1)]
发现跟自然语言中的26个字母出现的频率不接近,所以可以知道是适应度的问题,不能求出一个最佳的答案,故使用“爬山法”。
最后决定用爬山法完成以上代换密码的解密。有关quadgram statistics的适应度计算方法的详细介绍可点击这里。
(备注:quadgrams.txt和ngram_score.py可也在上面的链接中的文章最下方获取。其中ngram_score.py所用的函数不适用于python3.0,因为我试过T_T)
算法步骤:
①随机生成一个key,称为parentkey,用它解密得对应的明文m1,对明文计算适应度d1
②随机交换parentkey中的两个字符得到子密钥child,解密出对应的明文m2并计算适应度d2
③若d1
⑤回到①重新生成parentkey继续迭代寻找,或者由操作者终止程序
重新执行①,是为了防止②③的操作使结果陷入局部最优的困境。对于生成的明文的适应度的比较,其实可以看作是对不同解密密钥的比较,解密出来的明文的适应度越高,对应的密钥就更好。
quadgram statistics的适应度计算方法
算法思路:
因为整个密文都只是大写英文字母,所以并不需要进行字符转换操作。解密的时候,在生成了key之后,将key放入一个字典变量中,字典中每个变量都是“密文字符:明文字符”的映射对,从而对密文的字符进行一个接着一个地转换。循环嵌套有两层,外层是每次随机生成一个起始的parentkey,里层进行爬山法,每次随机交换parentkey里的两个元素以解密,最后每次外层循环都判断一次是否找到更优的密钥。
以下是main.py主程序:
# -*- coding: UTF-8 -*-
import random
from ngram_score import ngram_score
#参数初始化
ciphertext = 'JGRMQOYGHMVBJWRWQFPWHGFFDQGFPFZRKBEEBJIZQQOCIBZKLFAFGQVFZFWWEOGWOPFGFHWOLPHLRLOLFDMFGQWBLWBWQOLKFWBYLBLYLFSFLJGRMQBOLWJVFPFWQVHQWFFPQOQVFPQOCFPOGFWFJIGFQVHLHLROQVFGWJVFPFOLFHGQVQVFIEOGQILHQFQGIQVVOSFAFGBWQVHQWIJVWJVFPFWHGFIWIHZZRQGBABHZQOCGFHX'
parentkey = list('ABCDEFGHIJKLMNOPQRSTUVWXYZ')
#只是用来声明key是个字典
key = {'A':'A'}
#读取quadgram statistics
fitness = ngram_score('quadgrams.txt')
parentscore = -99e9
maxscore = -99e9
j = 0
print('---------------------------start---------------------------')
while 1:
j = j+1
#随机打乱key中的元素
random.shuffle(parentkey)
#将密钥做成字典
for i in range(len(parentkey)):
key[parentkey[i]] = chr(ord('A')+i)
#用字典一一映射解密
decipher = ciphertext
for i in range(len(decipher)):
decipher = decipher[:i] + key[decipher[i]] + decipher[i+1:]
parentscore = fitness.score(decipher)#计算适应度
#在当前密钥下随机交换两个密钥的元素从而寻找是否有更优的解
count = 0
while count < 1000:
a = random.randint(0,25)
b = random.randint(0,25)
#随机交换父密钥中的两个元素生成子密钥,并用其进行解密
child = parentkey[:]
child[a],child[b] = child[b],child[a]
childkey = {'A':'A'}
for i in range(len(child)):
childkey[child[i]] = chr(ord('A')+i)
decipher = ciphertext
for i in range(len(decipher)):
decipher = decipher[:i] + childkey[decipher[i]] + decipher[i+1:]
score = fitness.score(decipher)
#此子密钥代替其对应的父密钥,提高明文适应度
if score > parentscore:
parentscore = score
parentkey = child[:]
count = 0
count = count+1
#输出该key和明文
if parentscore > maxscore:
maxscore = parentscore
maxkey = parentkey[:]
for i in range(len(maxkey)):
key[maxkey[i]] = chr(ord('A')+i)
decipher = ciphertext
for i in range(len(decipher)):
decipher = decipher[:i] + key[decipher[i]] + decipher[i+1:]
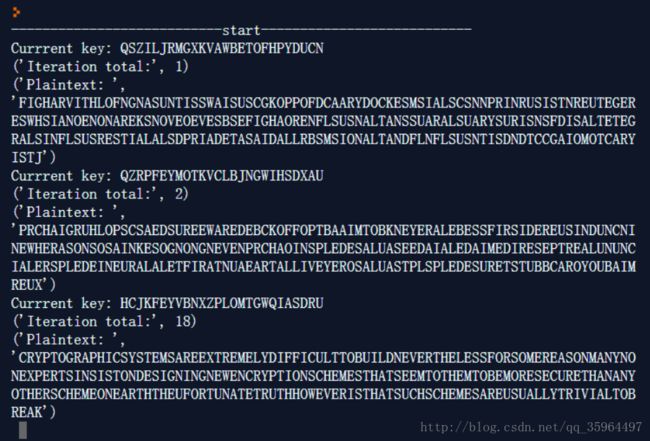
print ('Currrent key: '+''.join(maxkey))
print ('Iteration total:', j)
print ('Plaintext: ', decipher)算法结果:
可以看出,此算法效率还是比较高的,很快就可以得出比较令人满意的明文。
不过此算法还是有点可改进的地方,就是最后还得手动在单词之间和密文换行的时候添加空格,才可得出结果。
最后解得明文:
CRYPTOGRAPHIC SYSTEMS ARE EXTREMELY DIFFICULT TO BUILD NEVERTHELESS FOR SOME REASON MANY NON EXPERTS INSIST ON DESIGNING NEW ENCRYPTION SCHEMES THAT SEEM TO THEM TO BE MORE SECURE THAN ANY OTHER SCHEME ON EARTH THE UNFORTUNATE TRUTH HOWEVER IS THAT SUCH SCHEMES ARE USUALLY TRIVIAL TO BREAK