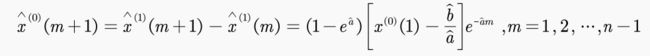预测模型——灰色预测模型及matlab代码实现
灰色预测的主要特点是模型使用的不是原始数据序列，而是生成的数据序列。其核心体系是灰色模型（Grey Model，简称GM），即对原始数据作累加生成（或其他方法生成）得到近似的指数规律再进行建模的方法。
优点是不需要很多的数据，一般只需要4个数据就够。缺点是只适合于中短期的预测，只适合指数增长的预测。
GM(1,1)预测模型1阶微分方程，只含1个变量
GM(1,1)模型预测步骤
1.数据的检验与处理
2.建立模型
3.检验预测值
（1）残差检验
（2）级比偏差检验
4.预测数据
灰色预测模型使用条件：
1.已知数据[x,y]的组合大于4组，小于10组。（已知的样本数据过小或过大可选择其他的方法预测）
2.在实际应用中，数据通常是以年份度量的非负数据（如果是月份或季度数据可用时间序列模型）
3.数据能经过准指数规律的检验（除了前两期外，后面至少90%的期数的光滑比要低于0.5）；
求解题型如下：
一、GM（1,1）模型原理
GM(1,1)模型，第一个‘1’表示微分方程是一阶的， 后面的‘1’表示只有一个变量。
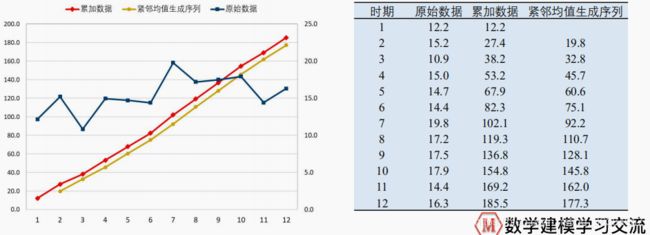
1、初始已知的非负序列设为x(0),求累加生成新的序列为x(1)，紧邻均值数列为z(1)。
三者的公式及例子如下：
对此简单解释如下：x(0)就是原始数据，x(1)是对原始数据的一次向后累加计算，z(1)是在x（1）基础上，求x(1)相邻元素平均值得到的。示例如下：
该图的左右侧的刻度不一样，原始数据使用的是右侧的刻度，累加数据和紧邻均值生成序列刻度使用的是左侧刻度。
2、求发展系数和灰作用量
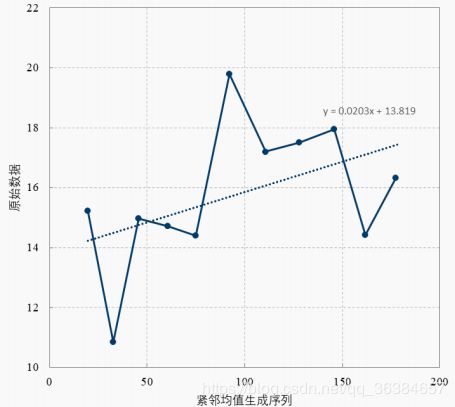
简而言之，就是让z(1)的值作为自变量x，x(0)的值作为因变量，就是根据这样一组数据点[z(1),x(0)]，求出线性回归方程（使用最小二乘法得到合适的曲线）。示例如下：
如图所示：z(1)作x轴，x(0)作y轴，通过最小二乘法求得一条直线，该直线的斜率k即为发展系数-a,截距b即为灰作用量。
3、求预测值
预测值用x(上面加个帽子^）表示，为什么还要求原始数据的预测值呢？因为我们要构建一个模型来预测后面的数据可能的情况，那么这个模型预测的结果和已知数据的差距越小越好，这个越小越好是通过残差检验和级比偏差检验判断的。
只需记住，预测值公式：
e就是普通的指数底数，-a是上一问求出的发展系数，b为灰作用量。x（0）（1）为原始序列中第一个元素，n为原始数据的长度。
4、准指数规律检验
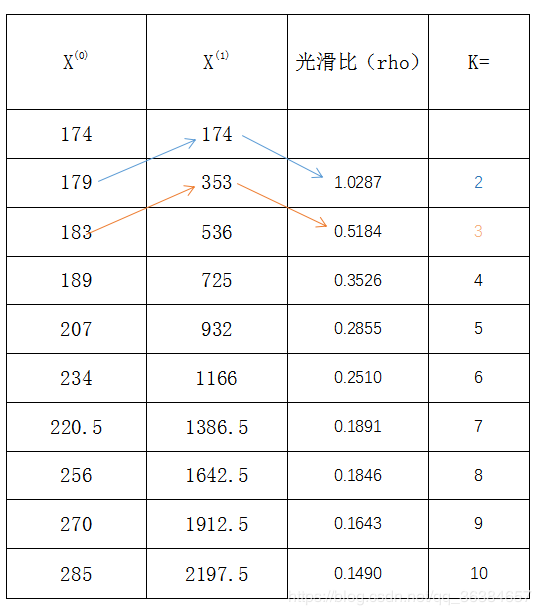
通过上式计算所有k>=2的数据的光滑比，示例如下：（假设有这样一组数据）
根据两个指标判断数据是否通过准指数规律检验：
指标1：光滑比小于0.5的数据占的比例（一般要大与60%才能通过检验）
指标2：除去前两个时期，光滑比小于0.5数据占的比例（一般要大于90%）
本示例中，光滑比小于0.5的数据占比为77.7778%（计算方法为7/9）；除去前两个时期外，光滑比小于0.5的数据占比为100%（计算方法为9/9），两种指标均通过准指数规律检验（其实就是看曲线是否光滑）
5、拟合效果检验——残差检验+级比残差检验
5.1残差检验
残差：真实值-预测值；相对残差：|真实值-预测值|/真实值；平均相对残差，对相对残差取均值
5.2级比残差检验
二、GM（1,1）拓展模型——新信息模型+新陈代谢模型
新信息模型主要是指预测的数据加入原始数据中，预测下一个数据。
新陈代谢模型是指预测的数据加入原始数据，同时，剔除原始数据首位元素。
具体见例题及代码部分。
三、灰色预测模型实例
例题依然用上述出现过的数据
（1）看到数据后先画时间序列图并简单的分析下趋势（例如时间序列分解）；
（2）将数据分为训练组和试验组，尝试使用不同的模型对训练组进行建模，并利用试验组的数据判断哪种模型的预测效果最好（比如我们可以使用SSE这个指标来挑选模型，常见的模型有指数平滑、ARIMA、灰色预测、神经网络等）。
（3）选择上一步骤中得到的预测误差最小的那个模型，并利用全部数据来重新建模，并对未来的数据进行预测。
（4）画出预测后的数据和原来数据的时序图，看看预测的未来趋势是否合理。
进入代码讲解，Let's go~
首先需要编写三个函数的m文件 ：gm11.m文件（原始的GM（1,1）模型）、new_gm11.m文件（新信息的GM（1,1）模型）、metabolism_gm11.m文件（新陈代谢GM（1,1）模型），最后是主函数main.m文件。（实验数据根据需要自己替换）
1、gm11.m文件
function [result, x0_hat, relative_residuals, eta] = gm11(x0, predict_num)
% 函数作用：使用传统的GM(1,1)模型对数据进行预测
% x0：要预测的原始数据
% predict_num： 向后预测的期数
% 输出变量 （注意，实际调用时该函数时不一定输出全部结果，就像corrcoef函数一样~，可以只输出相关系数矩阵，也可以附带输出p值矩阵）
% result：预测值
% x0_hat：对原始数据的拟合值
% relative_residuals： 对模型进行评价时计算得到的相对残差
% eta： 对模型进行评价时计算得到的级比偏差
n = length(x0); % 数据的长度
x1=cumsum(x0); % 计算一次累加值
z1 = (x1(1:end-1) + x1(2:end)) / 2; % 计算紧邻均值生成数列（长度为n-1）
% 将从第二项开始的x0当成y，z1当成x，来进行一元回归 y = kx +b
y = x0(2:end); x = z1;
% 下面的表达式就是第四讲拟合里面的哦~ 当是要注意，此时的样本数应该是n-1，少了一项哦
k = ((n-1)*sum(x.*y)-sum(x)*sum(y))/((n-1)*sum(x.*x)-sum(x)*sum(x));
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/((n-1)*sum(x.*x)-sum(x)*sum(x));
a = -k; %注意：k = -a哦
% 注意： -a就是发展系数, b就是灰作用量
disp('现在进行GM(1,1)预测的原始数据是: ')
disp(mat2str(x0')) % mat2str可以将矩阵或者向量转换为字符串显示
disp(strcat('最小二乘法拟合得到的发展系数为',num2str(-a),'，灰作用量是',num2str(b)))
disp('***************分割线***************')
x0_hat=zeros(n,1); x0_hat(1)=x0(1); % x0_hat向量用来存储对x0序列的拟合值，这里先进行初始化
for m = 1: n-1
x0_hat(m+1) = (1-exp(a))*(x0(1)-b/a)*exp(-a*m);
end
result = zeros(predict_num,1); % 初始化用来保存预测值的向量
for i = 1: predict_num
result(i) = (1-exp(a))*(x0(1)-b/a)*exp(-a*(n+i-1)); % 带入公式直接计算
end
% 计算绝对残差和相对残差
absolute_residuals = x0(2:end) - x0_hat(2:end); % 从第二项开始计算绝对残差，因为第一项是相同的
relative_residuals = abs(absolute_residuals) ./ x0(2:end); % 计算相对残差，注意分子要加绝对值，而且要使用点除
% 计算级比和级比偏差
class_ratio = x0(2:end) ./ x0(1:end-1) ; % 计算级比 sigma(k) = x0(k)/x0(k-1)
eta = abs(1-(1-0.5*a)/(1+0.5*a)*(1./class_ratio)); % 计算级比偏差
end2、new_gm11.m文件（调用了gm11函数）
function [result] = new_gm11(x0, predict_num)
% 函数作用：使用新信息的GM(1,1)模型对数据进行预测
% 输入变量
% x0：要预测的原始数据
% predict_num： 向后预测的期数
% 输出变量
% result：预测值
result = zeros(predict_num,1); % 初始化用来保存预测值的向量
for i = 1 : predict_num
result(i) = gm11(x0, 1); % 将预测一期的结果保存到result中
x0 = [x0; result(i)]; % 更新x0向量，此时x0多了新的预测信息
%根据预测值的增加序列长度不断增长，x0的长度也不断增加
end
end3、metabolism_gm11.m文件
function [result] = metabolism_gm11(x0, predict_num)
% 函数作用：使用新陈代谢的GM(1,1)模型对数据进行预测
% 输入变量
% x0：要预测的原始数据
% predict_num： 向后预测的期数
% 输出变量
% result：预测值
result = zeros(predict_num,1); % 初始化用来保存预测值的向量
for i = 1 : predict_num
result(i) = gm11(x0, 1); % 将预测一期的结果保存到result中
x0 = [x0(2:end); result(i)];
% 更新x0向量，此时x0多了新的预测信息，并且删除了最开始的那个向量，序列长度保持不变
end
end
4、main.m文件，代码内容如下：（很多都是代码提示语句，真正的执行语句不多的哦）
%% 输入原始数据并做出时间序列图
clear;clc
year =[1995:1:2004]'; % 横坐标表示年份，写成列向量的形式（加'就表示转置）
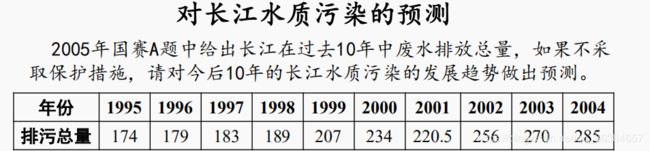
x0 = [174,179,183,189,207,234,220.5,256,270,285]'; %原始数据序列，写成列向量的形式（加'就表示转置）
n=length(x0);%计算原始数据的长度
% 画出原始数据的时间序列图
figure(1); % 因为我们的图形不止一个，因此要设置编号
plot(year,x0,'o-'); grid on; % 原式数据的时间序列图
set(gca,'xtick',year(1:1:end)) % 设置x轴横坐标的间隔为1
xlabel('年份'); ylabel('排污总量'); % 给坐标轴加上标签
%% 对一次累加后的数据进行准指数规律的检验(注意，这个检验有时候即使能通过，也不一定能保证预测结果非常，需要观察后面的趋势。
disp('准指数规律检验')
x1 = cumsum(x0); % 生成1-AGO序列，cumsum是累加函数哦~ 注意：1.0e+03 *0.1740的意思是科学计数法,即10^3*0.1740 = 174
rho = x0(2:end) ./ x1(1:end-1) ; % 计算光滑度rho(k) = x0(k)/x1(k-1)，x0从序号2开始到结束，x1从1开始到结束。（2：end)表示一个取值范围，相当于x0的取值是从下标2到最后一个下标
% 画出光滑度的图形，并画上0.5的直线，表示临界值
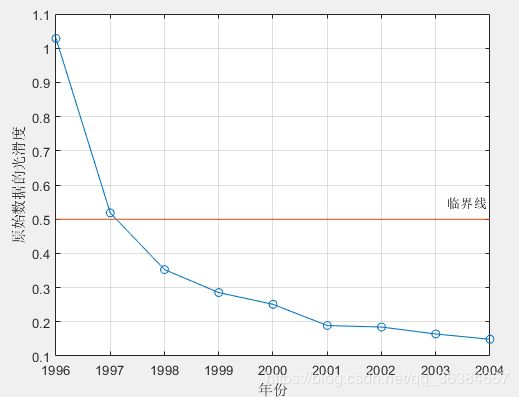
figure(2)
plot(year(2:end),rho,'o-',[year(2),year(end)],[0.5,0.5],'-'); grid on;
text(year(end-1)+0.2,0.55,'临界线') % 在坐标(year(end-1)+0.2,0.55)上添加文本
set(gca,'xtick',year(2:1:end)) % 设置x轴横坐标的间隔为1
xlabel('年份'); ylabel('原始数据的光滑度'); % 给坐标轴加上标签
disp(strcat('指标1：光滑比小于0.5的数据占比为',num2str(100*sum(rho<0.5)/(n-1)),'%'))
disp(strcat('指标2：除去前两个时期外，光滑比小于0.5的数据占比为',num2str(100*sum(rho(3:end)<0.5)/(n-3)),'%'))
Judge = input('你认为可以通过准指数规律的检验吗？可以通过请输入1，不能请输入0：');
if Judge == 0
disp('亲，灰色预测模型不适合你的数据哦~ 请考虑其他方法吧 例如ARIMA，指数平滑等')
ERROR = 1;
end
%% 当数据量大于4时，我们利用试验组来选择使用传统的GM(1,1)模型、新信息GM(1,1)模型还是新陈代谢GM(1,1)模型； 如果数据量等于4，那么我们直接对三种方法求一个平均来进行预测
if n > 4 % 数据量大于4时，将数据分为训练组和试验组(根据原数据量大小n来取，n为5-7个则取最后两年为试验组，n大于7则取最后三年为试验组)
disp('因为原数据的期数大于4，所以我们可以将数据组分为训练组和试验组') % 注意，如果试验组的个数只有1个，那么三种模型的结果完全相同，因此至少要取2个试验组
if n > 7
test_num = 3;
else
test_num = 2;
end
train_x0 = x0(1:end-test_num); % 训练数据
disp('训练数据是: ')
disp(mat2str(train_x0')) % mat2str可以将矩阵或者向量转换为字符串显示, 这里加一撇表示转置，把列向量变成行向量方便观看
test_x0 = x0(end-test_num+1:end); % 试验数据
disp('试验数据是: ')
disp(mat2str(test_x0')) % mat2str可以将矩阵或者向量转换为字符串显示
disp('------------------------------------------------------------')
% 使用三种模型对训练数据进行训练，返回的result就是往后预测test_num期的数据
disp(' ')
disp('***下面是传统的GM(1,1)模型预测的详细过程***')
result1 = gm11(train_x0, test_num); %使用传统的GM(1,1)模型对训练数据，并预测后test_num期的结果
disp(' ')
disp('***下面是进行新信息的GM(1,1)模型预测的详细过程***')
result2 = new_gm11(train_x0, test_num); %使用新信息GM(1,1)模型对训练数据，并预测后test_num期的结果
disp(' ')
disp('***下面是进行新陈代谢的GM(1,1)模型预测的详细过程***')
result3 = metabolism_gm11(train_x0, test_num); %使用新陈代谢GM(1,1)模型对训练数据，并预测后test_num期的结果
% 现在比较三种模型对于试验数据的预测结果
disp(' ')
disp('------------------------------------------------------------')
% 绘制对试验数据进行预测的图形（对于部分数据，可能三条直线预测的结果非常接近）
test_year = year(end-test_num+1:end); % 试验组对应的年份
figure(3)
plot(test_year,test_x0,'o-',test_year,result1,'*-',test_year,result2,'+-',test_year,result3,'x-'); grid on;
set(gca,'xtick',year(end-test_num+1): 1 :year(end)) % 设置x轴横坐标的间隔为1
legend('试验组的真实数据','传统GM(1,1)预测结果','新信息GM(1,1)预测结果','新陈代谢GM(1,1)预测结果') % 注意：如果lengend挡着了图形中的直线，那么lengend的位置可以自己手动拖动
xlabel('年份'); ylabel('排污总量'); % 给坐标轴加上标签
% 计算误差平方和SSE
SSE1 = sum((test_x0-result1).^2);
SSE2 = sum((test_x0-result2).^2);
SSE3 = sum((test_x0-result3).^2);
disp(strcat('传统GM(1,1)对于试验组预测的误差平方和为',num2str(SSE1)))
disp(strcat('新信息GM(1,1)对于试验组预测的误差平方和为',num2str(SSE2)))
disp(strcat('新陈代谢GM(1,1)对于试验组预测的误差平方和为',num2str(SSE3)))
if SSE15、运行结果
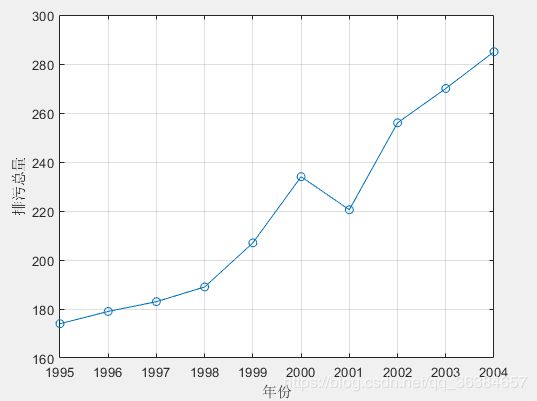图1.原始数据时间序列图
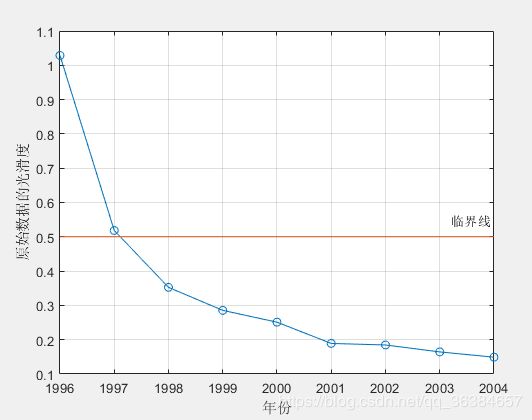图2.原始数据光滑比图
图3.测试样本的预测值与真实值曲线
图4.相对残差和级比残差走势曲线
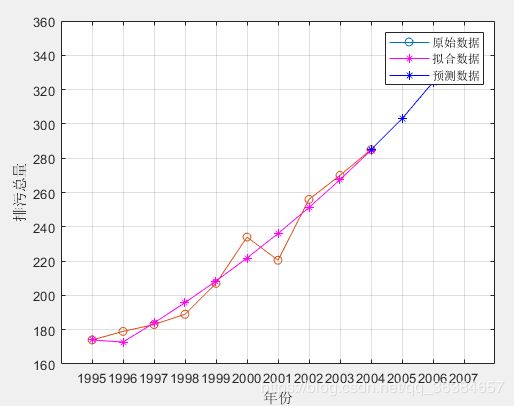图5.往后预测的三个数据与原始数据和拟合数据图
6、结果分析
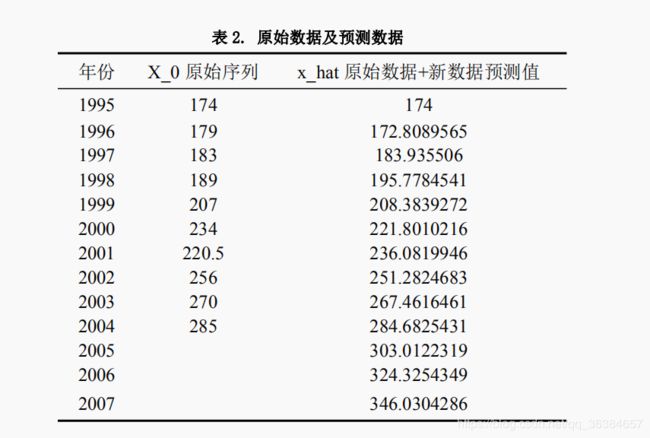
首先对上述10组数据进行了准指数规律检验，两种指标均通过检验，说明可以用灰色预测模型来进行问题求解；其次分别用了传统的GM（1,1）模型、新信息的GM(1,1)模型、新陈代谢GM（1,1）模型将10组数据分为了七个训练组合三个测试组，进行分析，因为新陈代谢模型的误差平方和最小，因此，我们选择该模型进行预测。新陈代谢GM（1,1）模型的特点是每步的原始数据是剔除一个头数据，加入一个预测的数据（这个预测的数据只是一个中间结果不作为最后的拟合值或预测值）。对该预测模型进行残差检验(<0.1)和级比偏差检验（<0.1），均通过，则灰色预测模型成功。以下是原始数据和拟合数据、预测数据的表格图。
最后的三个数据就是预测的结果了，也即题目的要求。灰色预测模型就是从少量原始数据出发，构建一个预测模型，不断的佐证其模型是可以使用的，且效果好，这样才能得到最后的预测结果。