【数学建模】灰色预测及Python实现

关键词：灰色预测、Python、pandas、numpy

一、前言

  本文的目的是用Python和类对灰色预测进行封装

二、原理简述

1.灰色预测概述

  灰色预测是用灰色模型GM(1,1)来进行定量分析的，通常分为以下几类：
    (1) 灰色时间序列预测。用等时距观测到的反映预测对象特征的一系列数量（如产量、销量、人口数量、存款数量、利率等）构造灰色预测模型，预测未来某一时刻的特征量，或者达到某特征量的时间。
    (2) 畸变预测（灾变预测）。通过模型预测异常值出现的时刻，预测异常值什么时候出现在特定时区内。
    (3) 波形预测，或称为拓扑预测，它是通过灰色模型预测事物未来变动的轨迹。
    (4) 系统预测，对系统行为特征指标建立一族相互关联的灰色预测理论模型，在预测系统整体变化的同时，预测系统各个环节的变化。
  上述灰色预测方法的共同特点是：
    （1）允许少数据预测；
    （2）允许对灰因果律事件进行预测，例如：
      灰因白果律事件：在粮食生产预测中，影响粮食生产的因子很多，多到无法枚举，故为灰因，然而粮食产量却是具体的，故为白果。粮食预测即为灰因白果律事件预测。
      白因灰果律事件：在开发项目前景预测时，开发项目的投入是具体的，为白因，而项目的效益暂时不很清楚，为灰果。项目前景预测即为灰因白果律事件预测。
    （3）具有可检验性，包括：建模可行性的级比检验（事前检验），建模精度检验（模型检验），预测的滚动检验（预测检验）。

 

2.GM(1,1)模型理论

  GM(1,1)模型适合具有较强的指数规律的数列，只能描述单调的变化过程。已知元素序列数据：

做一次累加生成（1-AGO）序列：

其中

，

令为的紧邻均值生成序列：

其中，

建立GM(1,1)的灰微分方程模型为：

其中，为发展系数，为灰色作用量。设为待估参数向量，即，则灰微分方程的最小二乘估计参数列满足

其中

再建立灰色微分方程的白化方程（也叫影子方程）：

白化方程的解（也叫时间响应函数）为

那么相应的GM(1,1)灰色微分方程的时间响应序列为：

取，

则

再做累减还原可得

即为预测方程。

注1：原始序列数据不一定要全部使用，相应建立的模型也会不同，即和不同；

注2：原始序列数据必须要等时间间隔、不间断。

3.算法步骤

(1) 数据的级比检验
  为了保证灰色预测的可行性，需要对原始序列数据进行级比检验。
  对原始数据列，

计算序列的级比：  

若所有的级比都落在可容覆盖内，则可进行灰色预测；否则需要对做平移变换，，使得满足级比要求。

(2) 建立GM(1,1)模型，计算出预测值列。

(3) 检验预测值：

① 相对残差检验，计算

  

若 ，则认为达到一般要求，若 ，则认为达到较高要求；

② 级比偏差值检验

  根据前面计算出来的级比, 和发展系数, 计算相应的级比偏差：

  

若, 则认为达到一般要求，若, 则认为达到较高要求。

(4) 利用模型进行预测。

三、程序实现

1.引入需要的包

import pandas as pd
import numpy as np

%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

  下面的matplotlib是作图用的，如果不做图可以不用引入

2.构建大致框架

  灰色建模的主体应该分为几步：
    （1）引入、整理数据
    （2）校验数据是否合格
    （3）GM(1,1)建模
    （4）将最新的预测数据当做真实值继续预测
    （5）输出结果
  因此打好的框架如下：

class GrayForecast():
#初始化
    def __init__(self, data, datacolumn=None):
        pass
#级比校验
    def level_check(self):
        pass
#GM(1,1)建模
    def GM_11_build_model(self, forecast=5):
        pass
#预测
    def forecast(self, time=5, forecast_data_len=5):
        pass
#打印日志
    def log(self):
        pass
#重置
    def reset(self):
        pass
#作图
    def plot(self):
        pass

3.__init__

  作为初始化的方法，我们希望它能将数据格式化存储，并且可使用的类型越多越好，在这里我先实现能处理三种类型：一维列表、DataFrame、Series。如果处理DataFrame可能会出现不止一维的情况，于是设定一个参数datacolumn，用于处理传入DataFrame不止一列数据到底用哪个的问题

def __init__(self, data, datacolumn=None):

    if isinstance(data, pd.core.frame.DataFrame):
        self.data=data
        try:
            self.data.columns = ['数据']
        except:
            if not datacolumn:
                raise Exception('您传入的dataframe不止一列')
            else:
                self.data = pd.DataFrame(data[datacolumn])
                self.data.columns=['数据']
    elif isinstance(data, pd.core.series.Series):
        self.data = pd.DataFrame(data, columns=['数据'])
    else:
        self.data = pd.DataFrame(data, columns=['数据'])

    self.forecast_list = self.data.copy()

    if datacolumn:
        self.datacolumn = datacolumn
    else:
        self.datacolumn = None
    #save arg:
    #        data                DataFrame    数据
    #        forecast_list       DataFrame    预测序列
    #        datacolumn          string       数据的含义

4.level_check

  按照级比校验的步骤进行，最终返回是否成功的bool类型值

def level_check(self):
    # 数据级比校验
    n = len(self.data)
    lambda_k = np.zeros(n-1)
    for i in range(n-1):
        lambda_k[i] = self.data.ix[i]["数据"]/self.data.ix[i+1]["数据"]
        if lambda_k[i] < np.exp(-2/(n+1)) or lambda_k[i] > np.exp(2/(n+2)):
            flag = False
    else:
        flag = True

    self.lambda_k = lambda_k

    if not flag:
        print("级比校验失败，请对X(0)做平移变换")
        return False
    else:
        print("级比校验成功，请继续")
        return True

#save arg:
#        lambda_k            1-d list

5.GM_11_build_model

  按照GM(1,1)的步骤进行一次预测并增长预测序列（forecast_list）
  传入的参数forecast为使用forecast_list末尾数据的数量，因为灰色预测为短期预测，过多的数据反而会导致数据精准度变差

def GM_11_build_model(self, forecast=5):
    if forecast > len(self.data):
        raise Exception('您的数据行不够')
    X_0 = np.array(self.forecast_list['数据'].tail(forecast))
#       1-AGO
    X_1 = np.zeros(X_0.shape)
    for i in range(X_0.shape[0]):
        X_1[i] = np.sum(X_0[0:i+1])
#       紧邻均值生成序列
    Z_1 = np.zeros(X_1.shape[0]-1)
    for i in range(1, X_1.shape[0]):
        Z_1[i-1] = -0.5*(X_1[i]+X_1[i-1])

    B = np.append(np.array(np.mat(Z_1).T), np.ones(Z_1.shape).reshape((Z_1.shape[0], 1)), axis=1)
    Yn = X_0[1:].reshape((X_0[1:].shape[0], 1))

    B = np.mat(B)
    Yn = np.mat(Yn)
    a_ = (B.T*B)**-1 * B.T * Yn

    a, b = np.array(a_.T)[0]

    X_ = np.zeros(X_0.shape[0])
    def f(k):
        return (X_0[0]-b/a)*(1-np.exp(a))*np.exp(-a*(k))

    self.forecast_list.loc[len(self.forecast_list)] = f(X_.shape[0])

6.forecast

  预测函数只要调用GM_11_build_model就可以，传入的参数time为向后预测的次数，forecast_data_len为每次预测所用末尾数据的条目数

def forecast(self, time=5, forecast_data_len=5):
    for i in range(time):
        self.GM_11_build_model(forecast=forecast_data_len)

7.log

  打印当前预测序列

def log(self):
    res = self.forecast_list.copy()
    if self.datacolumn:
        res.columns = [self.datacolumn]
    return res

8.reset

  初始化序列

def reset(self):
    self.forecast_list = self.data.copy()

9.plot

  作图

def plot(self):
    self.forecast_list.plot()
    if self.datacolumn:
        plt.ylabel(self.datacolumn)
        plt.legend([self.datacolumn])

四、使用

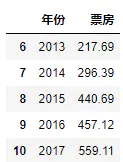
  首先读入数据，最近11年的电影票房

f = open("电影票房.csv", encoding="utf8")
df = pd.read_csv(f)
df.tail()

11条数据

 

  构建灰色预测对象，进行10年预测输出结果并作图

gf = GrayForecast(df, '票房')
gf.forecast(10)
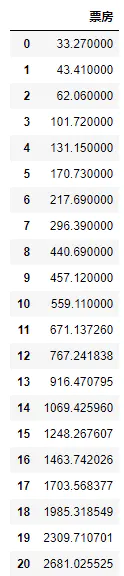
gf.log()

原来的11条数据+10条预测结果

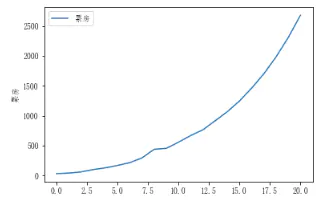
gf.plot()

全体数据作图

五、总结

  我们看数据的后面几条，高达数千万，或许10年前我们也想不到现在的电影票房是曾经原来的20倍。
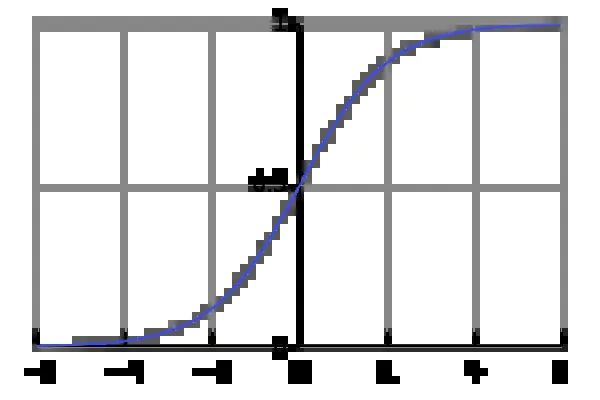
  这么快的增长已经接近指数增长了，然而它很可能就像人口一样，它并非是指数增长，而是没有达到增速减少的阈值罢了，用灰色预测很难看到如此长远的情况，或许可以将数据改为用sigmoid函数拟合，或许能达到更加准确的结果。

 

sigmoid函数

作者：crossous
链接：https://www.jianshu.com/p/a35ba96d852b
来源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。

https://blog.csdn.net/qq547276542/article/details/77865341/