如何在数组中间位置添加数组
首先提个问题,如何在数组中间位置添加数组?
<<数据结构与算法 javascript描述>>的写法:
function avaerageAdd(){
var nums = [1,2,3,4,5,6,7]
var newElements = [233,666]
nums.splice(Math.floor(nums.length / 2),0,newElements)
return nums
}
错误,实际输出//[1, 2, 3, Array[2], 4, 5, 6, 7]
它将数组作为一个元素插入,和问题不符,我们需要的是[1, 2, 3, 4, 233, 666, 5, 6, 7, 8]
因此可以修改代码如下:
function avaerageAdd(){
var nums = [1,2,3,4,5,6,7,8]
var newElements = [233,666]
nums.splice.apply(nums, [Math.floor(nums.length)/2, 0].concat(newElements))
return nums // [1, 2, 3, 4, 233, 666, 5, 6, 7, 8]
}
判定给定字符串是否回文
这涉及到堆栈。回文的意思是那么以某个字符为中心的前缀和后缀都是相同的.回文的判断非常简单,就是利用堆栈的特性,把字符串压入堆栈,然后弹出,这样顺序就和原字符串相反,再判断字符串是否和原字符串相等即可。
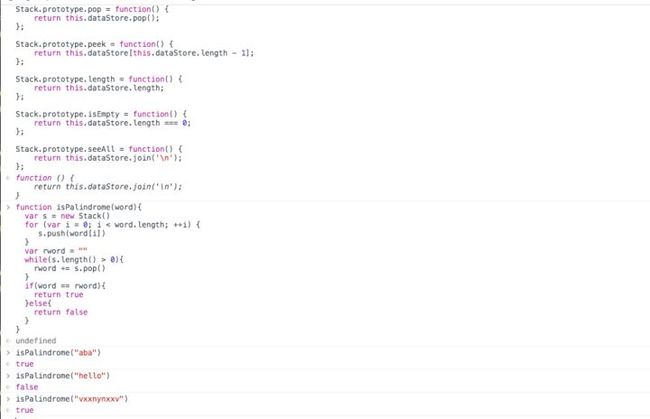
function isPalindrome(word){
var s = new Stack()
for (var i = 0; i < word.length; ++i) {
s.push(word[i])
}
var rword = ""
while(s.length() > 0){
rword += s.pop()
}
if(word == rword){
return true
}else{
return false
}
}
如何利用javascript构建Stack也很简单。将堆栈的特性用原型模式模拟出来即可。代码如下:
var Stack = function() {
this.dataStore = [];
this.top = 0;
};
Stack.prototype.push = function(element) {
this.dataStore.push(element);
};
Stack.prototype.pop = function() {
return this.dataStore.pop();
};
Stack.prototype.peek = function() {
return this.dataStore[this.dataStore.length - 1];
};
Stack.prototype.length = function() {
return this.dataStore.length;
};
Stack.prototype.isEmpty = function() {
return this.dataStore.length === 0;
};
Stack.prototype.seeAll = function() {
return this.dataStore.join('\n');
};
我们测试几个字符 aba hello vxxnynxxv
排序
冒泡排序
排序是基本功,冒泡排序更是常见,冒泡排序分两种,一种小泡泡往上吐,一种大泡泡往上吐。也就是从小到大和从大到小。
具体步骤:
冒泡排序就是从最开始的位置或结尾的位置反方向对比,如果比它大/小,就交换然后继续走,第一遍走完,最后一个位置是最大值或者最小值
根据上面我的描述很容易明白冒泡排序的时间复杂度是O(n^2),因为它是双重循环
而且它是稳定的。稳定的含义是:稳定排序算法会让原本有相等键值的纪录维持相对次序.
看代码:
function exchange(array, i, j) {
var t = array[i];
array[i] = array[j];
array[j] = t;
}
function bubbleSort(numbers) {
for (var i = 0; i < numbers.length; i++) {
for (var j = 0; j < numbers.length - i; j++) {
if (numbers[j] > numbers[j + 1]) {
exchange(numbers, j, j + 1);
}
}
console.log(numbers.toString())
}
return numbers;
}
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(bubbleSort(nums))
从代码中我们可以看到并没有对相等键值的两个元素进行处理。
对冒泡不太理解可以自己手写一下冒泡顺序然后和下面的图来对比一下:
快速排序
快速排序简称快排,基本上别人问你数据结构学过没,都会让你手写个快排看看。
快排就是一开始找个中介,然后把比它小的放左边,比它大的放右边,然后重新对中介两边的数据各自重新找个中介,如此循环。
function quickSort(arr) {
if (arr.length <= 1) { return arr }
console.log("原数组是:" + arr)
var pivotIndex = Math.floor(arr.length / 2)
var pivot = arr.splice(pivotIndex, 1)[0]
var left = []
var right = []
console.log("将中介提取出来后数组是:" + arr)
for (var i = 0 ; i < arr.length ; i++){
console.log("此刻中介是:" + pivot + "当前元素是:" + arr[i])
if (arr[i] < pivot) {
left.push(arr[i])
console.log("移动" + arr[i] + "到左边")
} else {
right.push(arr[i])
console.log("移动" + arr[i] + "到右边")
}
}
return quickSort(left).concat([pivot], quickSort(right))
}
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(quickSort(nums))
在脑中循环一下就知道用递归来写最容易理解。
快排的时间复杂度是O(nlogn),属于不稳定的排序
选择排序
找到数组中最小的那个元素,将它和数组的第一个元素交换位置,
如果第一个元素就是最小的那么就和自己交换
然后,在剩下的数组中找到最小的元素,将它和数组的第二个元素交换
循环直到排序完成。
内循环只比较大小,交换代码在内循环之外
每次交换都排定一个元素,交换的总次数为N
选择排序比较简单,看描述就能理解。
function selectionSort(numbers) {
for (var i = 0; i < numbers.length; i++) {
var min = i;
for (var j = i + 1; j < numbers.length; j++) {
if (numbers[j] < numbers[min]) {
min = j;
}
}
if (i !== min) {
exchange(numbers, i, min);
}
}
return numbers;
}
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(selectionSort(nums))
选择排序的时间复杂度是O(n²),也是不稳定的排序。
插入排序
插入排序它将数组分成“已排序”和“未排序”两部分,一开始的时候,“已排序”的部分只有一个元素,然后将它后面一个元素从“未排序”部分插入“已排序”部分,从而“已排序”部分增加一个元素,“未排序”部分减少一个元素。以此类推,完成全部排序。
function insertionSort(numbers) {
console.log("原数组:" + numbers)
for (var i = 0; i < numbers.length; i++) {
/*
* 当已排序部分的当前元素大于value,
* 就将当前元素向后移一位,再将前一位与value比较
*/
for (var j = i; j > 0 && numbers[j] < numbers[j - 1]; j--) {
// If the array is already sorted, we never enter this inner loop!
exchange(numbers, j, j - 1);
console.log("此时数组:" + numbers)
}
}
return numbers;
};
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(insertionSort(nums))
插入排序的空间复杂度是O(n²),而且它是稳定的排序
希尔排序
希尔排序属于高级排序,因为它其实是利用了多个插入排序来实现。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序
假设nums = [2,3,4,3,1,5,7,122,341,-1]
如果间隔为3,第一趟将数组下标为 0,4,8 || 1,5,9 || 2,6,10 || 3,7, 分别取出来子序列内部进行排序
然后缩小间隔再排序直到间隔为1时,全部直接插入排序
function shellsort(numbers) {
console.log("原数组:" + numbers)
var h = 1;
while (h < numbers.length / 3) {
h = (3 * h) + 1;
}
while (h >= 1) {
console.log("此时h:" + h)
for (var i = h; i < numbers.length; i++) {
for (var j = i; j >= h && numbers[j] < numbers[j - h]; j -= h) {
exchange(numbers, j, j - h);
console.log("此时数组:" + numbers)
}
}
h = --h / 3;
}
return numbers;
}
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(shellsort(nums))
希尔排序当时上课学的时候其实都用纸笔来进行笔算。这样记忆比较深刻。希尔排序的间隔是可以自己指定的,一般传统都是以3开始。
它属于不稳定的排序,时间复杂度为O(nlog^2*n)
归并算法
归并算法的原理是将所有元素拆成相邻的一对一对的,然后两两排序,再将相邻的一对元素再合并排序,四个四个排序,如此循环最后只剩两组大的已经排好序的数组再合并一起排序。
它依赖归并操作,归并操作即:将两个已经排序的序列合并成一个序列的操作。
function mergeSort(numbers) {
if (numbers.length < 2) {
return numbers;
}
var middle = Math.floor(numbers.length / 2),
left = numbers.slice(0, middle),
right = numbers.slice(middle),
params = merge(mergeSort(left), mergeSort(right));
params.unshift(0, numbers.length);
numbers.splice.apply(numbers, params);
return numbers;
function merge(left, right) {
var result = [],
il = 0,
ir = 0;
while (il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++]);
}
}
return result.concat(left.slice(il)) .concat(right.slice(ir));
}
}
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(mergeSort(nums))
归并排序的时间复杂度为O(nlogn),而且需要需要O(n)额外空间,它属于稳定的排序。
搜索
对于搜索其实一开始没必要掌握复杂的,循环,正则掌握就能应付基本的需求。
二分搜索
二分查找是基本功,而且需要注意的是,二分查找的前提是数组一开始就是有序的。
function binSearch(arr, data) {
arr = arr.sort(function(a, b) {
return a - b;
})
console.log(arr)
var upperBound = arr.length-1;
var lowerBound = 0;
while (lowerBound <= upperBound) {
var mid = Math.floor((upperBound + lowerBound) / 2);
console.log("Current midpoint: " + mid);
if (arr[mid] < data) {
lowerBound = mid + 1;
}
else if (arr[mid] > data) {
upperBound = mid - 1;
}
else {
return mid;
}
}
return -1;
}
var nums = [2,3,4,3,1,5,7,122,341,-1]
console.log(binSearch(nums,122))