【源码】移动边缘计算卸载机制MEC Offloading Python(Matlab)仿真
之前看了一个移动边缘计算的三级卸载方案,然后打算做一个仿真,论文名如下
《Energy-efficient Offloading for Mobile Edge Computing in 5G Heterogeneous Networks》
由于文中涉及的变量和公式过多,导致仿真异常难做
这里整理出几个问题和大家一起讨论
已经做好的代码见下文,历时10天(中间有大大小小的事情)
由于本文的变量较多,而且目前在度娘和github也搜不到数据集
所以,所有的数据都是我假设出来的,通过随机函数给出
分配信道的过程不好量化就省略了
本文出现的疑问将会持续更新。
1、任务是原子级的,不可进一步划分
2、MEC服务器允许多个计算任务同时进行
3、回传的功耗是忽略的,因为回传是与其他基础设施共享的
4、SBS到底经不经过MBS,文中说的不经过(用的or),但是要回传干什么
5、功率调节机制可参照参考文献【36】
6、设备所需的总信道数应该小于MBS和SBS共有的信道数
7、选择了SBS就不能选其他的,选择本地和MBS和local也是同理
8、一个迭代阶段,一个任务只能选择一个信道传输至MBS
9.每个MBS信道的发射功率相同,不同的信道不同的只能是信道增益
伪代码
#include真正的代码如下: 目前已做出来第一级卸载机制
当然目前也遇到了不少问题
问题:
1、回传机制是啥样的,为什么小基站传大基站没有能耗
2、ps gs pm gm大基站小基站传输的信道增益和信道功率未知
3、卸载机制二中,总传输速度是怎么算的
4、信道分配问题,为什么二三级卸载机制只处理待处理集,那些在第一级已经确定的设备优先选择信道吗?(并行问题)
5、第三级卸载机制中,为什么p最小的先选信道
# -*- coding: utf-8 -*-
"""
Created on Sun Dec 22 11:28:38 2019
@author: han
"""
import numpy as np
import matplotlib.pyplot as plt
from math import log
import operator
###正常情况无卸载机制###
el=np.random.randint(1,10,100) #一个cpu周期的本地的能耗
y=[]
cl=np.random.randint(1,10,100)#计算此任务所需的能力,能cpu周期规划
d =np.random.randint(300,800,100)#每个计算任务的大小
x = np.linspace(10,100,10,dtype=int)#x个移动设备
print(x)
for i in x:
print(i)
sum=0
for j in range(i):
sum = sum+(2*cl[j]*el[j])/100
# print(sum)
y.append(sum);
print(y)
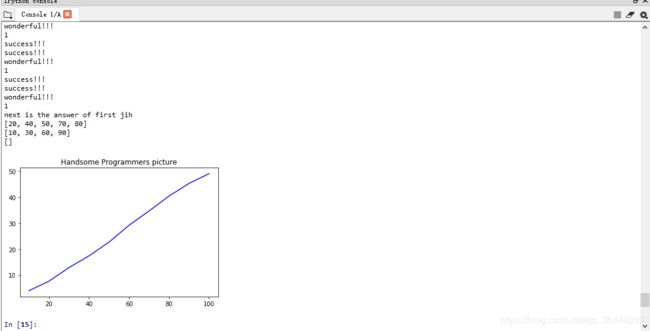
plt.plot(x,y,color='blue',linestyle='-')
plt.title('Handsome Programmers picture')
###第一级卸载机制如下###
pl=np.random.randint(1,10,100)
tl=[]#本地计算任务消耗时间
GR=[]#传给MEC服务器的设备集合
GL=[]#本地计算任务的集合
GO=[]#继续筛选的集合
le=[]#单个任务本地消耗的能耗
ns=[]#在小基站计算的设备数目
nm=[]#在大基站计算的设备数目
L=[]
def findMin(alist):
findMin = alist[0];
for i in range(1,len(alist)):
if alist[i] < findMin:
findMin = alist[i]
return findMin
tl = (cl*10.0)//pl############## deadline和tmax的精度不对
dead=np.random.randint(5,10,100)
print(x)
for k in x:
if k==100:
break;
if tl[k] > dead[k]:
print('success!!!')
GR.append(k)
elif tl[k]<=dead[k]:
le = cl*el
print('wonderful!!!')
ns=d/((dead-cl/4)*log((1+40),2))#【【大基站和小基站的传输功率未知这里统一成20W】】
nm=d/((dead-cl/4)*log((1+80),2))#【【大基站和小基站的传输功率未知这里统一成20W】】
L=[ns[k],nm[k]]
p=findMin(L)
if el[k]<p:
GL.append(k)
print('1')
else:
GO.append(k)
print('2')
print('next is the answer of first jih')
print(GR)
print(GL)
print(GO)
##第二级卸载机制##
##第三级卸载机制##
最后的结果,做出前两级机制,并没有考虑第三级信道的分配
大体图已经画出
由于信道不好量化就省略了第二级和第三级卸载机制
目前拟理解是分配信道的量化是通过速度来衡量,不同的信道速度不同
# -*- coding: utf-8 -*-
"""
Created on Sun Dec 22 11:28:38 2019
@author: han
"""
import numpy as np
import matplotlib.pyplot as plt
from math import log
###正常情况无卸载机制###
el=np.random.randint(1,10,100) #一个cpu周期的本地的能耗
y=[]
cl=np.random.randint(1,10,100)#计算此任务所需的能力,能cpu周期规划
d =np.random.randint(300,800,100)#每个计算任务的大小
x = np.linspace(10,100,10,dtype=int)#x个移动设备
print(x)
for i in x:
print(i)
sum=0
for j in range(i):
sum = sum+(2*cl[j]*el[j])/100#加了个2调整系数
# print(sum)
y.append(sum);
print(y)
plt.plot(x,y,color='blue',linestyle='-')
plt.title('Handsome Programmers picture')
###########第一级卸载机制如下###############
pl=np.random.randint(1,10,100)#扩大了10倍,使用的时候请注意,本地功率
tl=[]#本地计算任务消耗时间
GR=[]#传给MEC服务器的设备集合
GL=[]#本地计算任务的集合
GO=[]#继续筛选的集合
le=[]#单个任务本地消耗的能耗
ns=[]#在小基站计算的设备数目
nm=[]#在大基站计算的设备数目
L=[]
p={}
def findMin(alist):
findMin = alist[0];
for i in range(1,len(alist)):
if alist[i] < findMin:
findMin = alist[i]
return findMin
tl = (cl*10.0)//pl# deadline和tmax的精度不对,已修正
dead=np.random.randint(5,10,100)
print(x)
for i in range(0,99):
print('this i is=====',i)
if tl[i] > dead[i]:
print('success!!!')
GR.append(i)
elif tl[i]<=dead[i]:
le = cl*el
print('wonderful!!!')
ns=d/((dead-cl/4)*log((1+40*20/100),2))#{论文里的公式}【【大基站和小基站的传输功率未知这里统一成20W】】??背景噪声功率
nm=d/((dead-cl/4)*log((1+80*20/100),2))#{论文里的公式}【【大基站和小基站的传输功率未知这里统一成20W】】??背景噪声功率
L=[40*ns[i],80*nm[i]] #warning!40和80的单位,而且忘记乘10000
c=findMin(L)
p[i]=c/100#调整系数
if el[i]<p[i]:
GL.append(i)
print('GL!')
elif el[i]>=p[i]:
GO.append(i)
print('2')
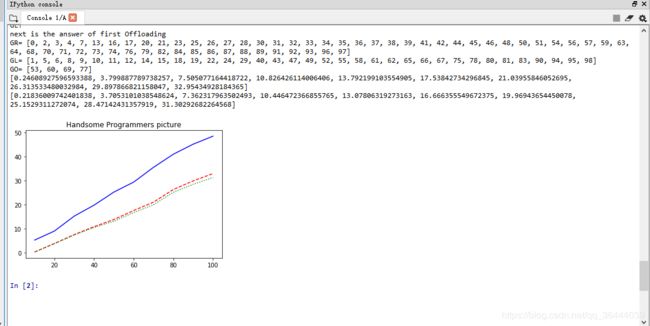
print('next is the answer of first Offloading')
print('GR=',GR)
print('GL=',GL)
print('GO=',GO)
###########第二级卸载机制############
#图中第二条线
len1=len(GR)
len2=len(GL)
len3=len(GO)
z=[]
v=[]
test=[]
sum1=0
sum2=0
for i in range(0,99):
#sum1=0
for j in range(len1):
if GR[j]==i:
r=log((1+40*20/100),2)
sum1 = sum1+(d[i]/r+cl[i]*0.0001)/1500###warning 1500准备调节
sum2 = sum2+(d[i]/r+cl[i]*0.0001)/1500###warning 1500准备调节
# print('ONE SUM',sum1)
break;
for j in range(len2):
if GL[j]==i:
r=log((1+80*20/100),2)
sum1 = sum1+(2*cl[i]*el[i])/100 #加了个调节系数的2
sum2 = sum2+(2*cl[i]*el[i])/100 #加了个调节系数的2
# sum1 = sum1+(2*d[i]/r+cl[i]*0.0001)/1000###warning 1000准备调节,2是大基站的p
#=print('TWO SUM',sum1)
break;
sum1 = sum1+(d[i]/r+cl[i]*0.0001)/800###warning 1500准备调节
rm=log((1+80*20/100),2)
rs=log((1+40*20/100),2)
tm = d/rm+c/4
ts = d/rs+d*0.0001+c/4
if tm[i] < ts[i]:
sum2 = sum2+(2*d[i]/rm+cl[i]*0.0001)/1500###warning 1000准备调节,2是大基站比小基站多的
else:
sum2 = sum2+(d[i]/rs+cl[i]*0.0001)/1500###warning 1000准备调节
# print('THREE SUM',sum1)
#print(sum)
if i==0 or (i+1)%10==0:
z.append(sum1);
v.append(sum2);
print(z)
print(v)
plt.plot(x,z,color='red',linestyle='--')
plt.plot(x,v,color='green',linestyle=':')
###########第二级卸载机制############
###因为不知道信道怎么根据任务大小而分配,难道和信道增益有关?
##分配好了之后,再怎么量化考虑?
###########信道数未考虑##########
#rm=[]#速率
#rs=[]#速率
#leng=len(GO)
#rm[i]=log((1+40),2)
#ct=2**(d[i]/dead[i]-rm[i])-1
#snr=#信噪比
##第三级卸载机制##
###########第三级卸载机制############
########第三条线#########