AD(阿尔茨海默病)诊断初解
本篇博文主要参考来源于太原理工大学硕士研究生秦嘉玮的硕士学位论文《MRI 结构特征选择方法及 AD 早期诊断的应用研究》,也是博主的AD第一篇学习论文。在本文中主要介绍AD诊断的背景及其特征选择方法。
- AD诊断的背景
- 特征选择的基础理论
- 启发式搜索特征选择模型
- MRI数据预处理
写了这篇论文笔记之后我再也不会写学位论文笔记了,简直是太长了,要写就写他对应的学术论文的笔记了,这样创新点比较容易get,只用写结构和它的创新点就行了!不然还得分析一大堆!
AD的背景及其研究现状
阿尔茨海默病(Alzheimer’s Disease,AD),又称老年痴呆症,这种疾病会影响患者的记忆力、理解力、认知能力等等,给家庭和社会带来很大负担,而且病因和发病机制还不明确,目前没有有效的治疗方法。轻度认知障碍(Mild Cognitive Impairment,MCI)是 AD 的早期过程。有研究发现对 MCI 患者或者早期 AD 患者进行药物干预,可以改善症状、缓解病情。因此,对 MCI、AD 患者的早期诊断显得尤为重要。
核磁共振成像是常用的一种 MCI、AD 诊断技术,但受到技术限制,MCI、AD 的MRI 图像目前还主要依靠医生经验人工判断,尚未实现自动诊断。如何实现 MCI、AD的自动诊断是计算机、人工智能、医学影像等相关领域的研究热点之一。通过对 MRI图像的深入研究,挖掘其包含的有用信息,可以得到灰质体积、白质容积、脑脊液容积等大量的脑结构信息。那么,如何将这些特征运用到 MCI、AD 的分类研究中就成了提高其诊断准确率的关键。
由于脑部结构比较复杂,对于需要的特征进行选择这是研究的重点,也是难点。特征有“无关特征”(与当前学习任务无关)和“冗余特征”(所包含的信息可以从其他特征推演出来)!对于已知类型的样本进行特征选择无外乎以下几种:基于错误率进行选择,根据分类器的错误率从原始特征中选择数目固定的特征子集,错误率最小的特征即为最优特征子集;基于维度进行特征选择,即规定一个分类器的错误率,从原始特征中选择维度最小的特征子集;在二者之间做一个折中,考虑错误率和特征维度两方面因素。
近年来,特征选择算法的研究飞速发展,其关键在于研究特征选择与特征提取相融合的特征选择算法、筛选出分类效果最优的特征子集以及研究如何将 Filter 过滤式模型和 Wrapper 封装式模型(下一节介绍这2个模型)更好融合这三方面。
神经影像学检查已经广泛地应用于 MCI、AD 的辅助诊断,其中主要包含结构影像学检查和功能影像学检查。MRI 图像通过磁共振成像技术生成,扫描时间较短,而且图像包含了人体的很多信息,对这些信息进行探索和研究是准确诊断 MCI、AD 患者的关键。
人脑结构是错综复杂的,正常衰老也会伴随着脑结构的萎缩,MCI、AD 患者也存在脑区萎缩的现象,这就给临床诊断带来了许多困难:到底哪些脑区的萎缩是患病造成的,哪些脑区的萎缩只是正常衰老。正确判断脑结构的变化能有效地诊断出 MCI、AD患者,但是现在对于 MCI、AD 的诊断主要还是依靠阅片医生的主观判断,这样的方法耗时耗力,而且还存在一定的主观性,会影响疾病的诊断准确性。如何自动准确的诊断MCI、AD 成为了现阶段研究的热点,该论文提出 HS-EJ (启发式搜索特征选择模型)特征选择模型,对脑图像中大量的信息进行筛选,提取有用的信息,用于 MCI、AD 的自动诊断。
该论文采集了NC、MCI、AD的MRI数据,提取所有的被试的灰质,白质,和脑脊液体积进行特征选择并分类,评估特征选择方法的优劣。

特征选择的基础理论
该论文的创新就在于特征选择模型的融合这一块,在这节主要介绍几个基础理论,这也是博主的小小理解,已经学习过的也可以看一下,不足之处请多多指教!
Dash 等人分析了大量特征选择方法之后,提出了一种如下图 所示的通用的特征选择过程,包括子集生成、子集评价、停止条件以及结果验证四部分!
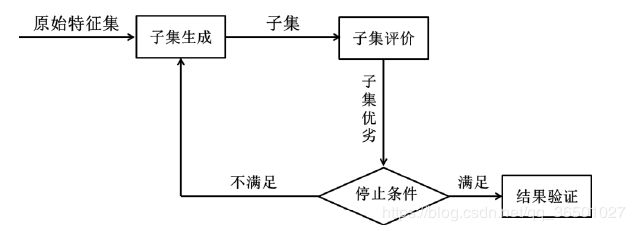
特征选择的一般过程:首先是对原始的特征进行子集选择,将原始特征分为多个子集,为下一步的子集评价做准备;然后进入子集评价环节,将多个特征子集依次进行子集评价,然后输出结果,根据停止条件选择出最优特征子集;最后将这组特征进行实际检测。
- 子集生成
特征子集主要由特征子集搜索方向决定的,常见的搜索方向有以下几种:
前向搜索:初始化特征子集,依次将特征加入循环当中进行子集评价,直到选择出满足条件的特征子集,这就是最优特征子集。
后向搜索:将原始特征依次减少特征加入循环,直到满足条件为止,得到最优特征子集。
双向搜索:结合前向和后向搜索的思想,从两个方向同时进行搜索,得到最优特征子集。相比较前向和后向搜索,双向搜索用时较短。
随机搜索:随机选择初始特征子集,然后随机选出特征进入循环,得到最优特征子集。但这样的方法可能会陷入局部最优中,而且多次运行得到的特征子集可能存在较大差异。 - 子集评价
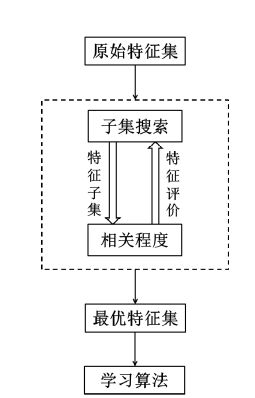
子集评价是特征选择过程中最关键的一环,主要作用是评价产生过程中所提供的特征子集的好坏,按照其工作原理可以分为 Filter 过滤式模型和 Wrapper 封装式模型。
Filter 过滤式模型
Filter 过滤式模型的评估算法与后续的学习算法分开的,也就是说是直接由数据求的,不依赖学习算法。这种模型只依赖数据本身,运用特征的相关程度进行特征选择,特征相关度较大的特征认为有较好分类效果的特征。
该模型的通用性强,可用于不同的特征集,而且算法简单,易于操作,适用于数据量较大的特征集。但是其忽略了后续的学习算法,选出的特征可能对于学习算法不是最优的特征集,因此得到的分类效果可能不是最优的。
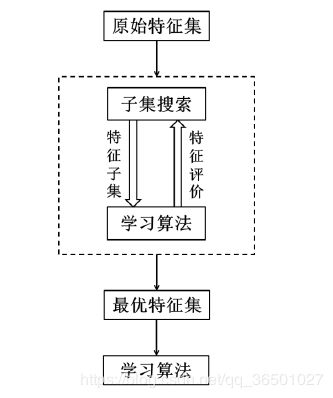
Wrapper 封装式模型
Wrapper 封装式模型的评估算法是考虑后续的学习算法,以学习算法的性能作为评价标准,一般为分类准确率。通过后续学习算法选择出的最优特征集,不仅得到特征子集,而且考虑了学习算法对特征的影响
这样的模型得到的最优特征子集能显著提高学习算法的性能,但是每一次子集评价时都需要
学习算法的参与,时间复杂度较高。
-
评价标准
Filter 过滤式特征选择模型一般基于以下四种评价标准进行特征选择:相关性、距离、信息增益以及一致性度量标准,Wrapper 封装特征选择模型以学习算法的性能作为评价标准,因此多运用分类准确率作为度量指标。直接运用分类准确率作为特征选择的评价标准有利于提升后续学习算法的性能,准确性极高。 -
停止条件与结果验证
特征选择过程是一个循环过程,如果没有停止的话,这个循环将无穷无尽的循环下去,因此需要一个停止条件。当循环满足这一条件时,特征子集搜索过程停止,输出最优特征子集。一般停止条件的设置遵循以下几条规定:达到一定的分类准确率的特征集;特征数增加或者减少时不会改变原有的结果时得到的特征集。结果验证就是验证最优特征子集的有效性,具体方法一般是运用分类算法验证其是否能提高分类准确率。因此,如果能保留两种模型的优点,去除其缺点,可能提高特征选择模型的性能。
启发式搜索特征选择模型
- 显著性分析
“显著性检验”实际上是英文significance test的汉语译名。在统计学中,显著性检验是“统计假设检验”(Statistical hypothesis testing)的一种,显著性检验是用于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。实际上,了解显著性检验的“宗门背景”(统计假设检验)更有助于一个科研新手理解显著性检验。“统计假设检验”这一正名实际上指出了“显著性检验”的前提条件是“统计假设”,换言之“无假设,不检验”。任何人在使用显著性检验之前必须在心里明白自己的科研假设是什么,否则显著性检验就是“水中月,镜中花”,可望而不可即。用更通俗的话来说就是要先对科研数据做一个假设,然后用检验来检查假设对不对。一般而言,把要检验的假设称之为原假设,记为H0;把与H0相对应(相反)的假设称之为备择假设,记为H1。
如果原假设为真,而检验的结论却劝你放弃原假设。此时,我们把这种错误称之为第一类错误。通常把第一类错误出现的概率记为α
如果原假设不真,而检验的结论却劝你不放弃原假设。此时,我们把这种错误称之为第二类错误。通常把第二类错误出现的概率记为β
通常只限定犯第一类错误的最大概率α, 不考虑犯第二类错误的概率β。我们把这样的假设检验称为显著性检验,概率α称为显著性水平。显著性水平是数学界约定俗成的,一般有α =0.05,0.025.0.01这三种情况。代表着显著性检验的结论错误率必须低于5%或2.5%或1%(统计学中,通常把在现实世界中发生几率小于5%的事件称之为“不可能事件”)。(以上这一段话实际上讲授了显著性检验与统计假设检验的关系)。
有过机器学习基础的同学可以把“元”和“因素”分别理解成机器学习中的“特征个数”和“标签个数”。拥有多个特征便是“多元”,而拥有多个标签便是“多因素”。
通过显著分析法,可以得到两组之间引起差异的特征,从而简化特征!
- Logistic 回归分析
线性回归用来预测,逻辑回归用来分类。
线性回归是拟合函数,逻辑回归是预测函数
线性回归的参数计算方法是最小二乘法,逻辑回归的参数计算方法是梯度下降
Logistic 回归分析的系数是由最大似然估计法得到的,这样就保证了在某一特定特异度下可获得最大灵敏度,或在某一特定灵敏度下可获得最大特异度,从而能得到最大的分类准确率。通过这样的方法进行特征选择可有效地降低特征间的冗余,对特征间的交互关系深入分析,从而起到去伪存真的效果。Logistic 回归被广泛地应用于医学领域。
- 多元线性回归模型
多元线性回归是反映一种现象或事物的数量依赖多种现象或事物的数量的变动而相应地变动的规律,建立多个变量之间线性数学模型数量关系式的统计方法。在实际问题中,影响一个事物的因素往往不止一个,而是很多个,也就是说因变量对应着多个自变量。在多元回归分析没有普及的时候,遇到这种问题往往只能考虑各个自变量单独对因变量的影响。如果用多元回归处理这样的问题时,可以将所有的自变量加入回归模型,综合分析自变量与因变量之间的相互作用。 - ROC曲线
二分类问题在机器学习中是一个很常见的问题,经常会用到。ROC (Receiver Operating Characteristic) 曲线和 AUC (Area Under the Curve) 值常被用来评价一个二值分类器 (binary classifier) 的优劣,也就是研究学习器的泛化能力的强弱。
ROC 曲线将灵敏度和特异度结合在一起得出准确率,可准确反映某一特征对于两类的分类能力。
但是,由于 ROC 曲线基于两类变量进行分类,所以该方法只适用于二分类,无法实现多分类的研究。 - 基于经验判断的启发式搜索特征选择模型
基本原理是结合Filter过滤式模型和Wrapper封装式模型进行特征选择。根据经验判断可知,显著性水平越高的特征,分类效果就越好;反之,显著性水平越低的特征,分类效果就越差。通过这样的方法过滤掉分类效果较差的
特征,然后运用SVM封装式模型进行进一步的特征选择,使用SVM分类器的分类准确率作为评价指标,得到最优特征子集。
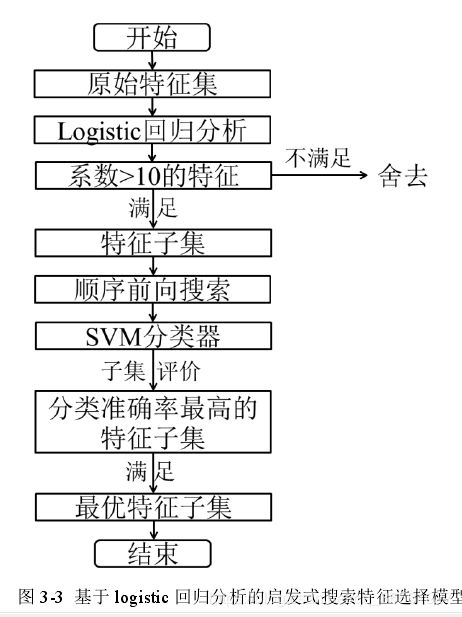
根据经验判断可知,logistic 回归分析系数越高的特征,分类效果就越好;反之,logistic 回归分析系数越低的特征,分类效果就越差。将 logistic 回归分析过滤模型代替显著性分析过滤模型,过滤掉分类效果较差的特征,然后运用 SVM 封装式模型,使用SVM 分类器的分类准确率作为评价指标,得到最优特征子集。