【ICLR2019】DARTS代码解读
DARTS:DIFFERENTIABLE ARCHITECTURE SEARCH
- 推荐阅读
- cnn (for cifar10)
- architect.py
- genotypes.py
- model_search.py
- train_search.py
- utils.py
推荐阅读
Source Code
解读参考
公式推导
cnn (for cifar10)
主要对影响理解的代码做以解释
architect.py
该函数是为了求alpha的导数而设置。
class Architect(object):
#计算alpha的梯度
def __init__(self, model, args):
self.network_momentum = args.momentum
self.network_weight_decay = args.weight_decay
self.model = model
self.optimizer = torch.optim.Adam(self.model.arch_parameters(), #训练路径参数alpha
lr=args.arch_learning_rate, betas=(0.5, 0.999), weight_decay=args.arch_weight_decay)
def _compute_unrolled_model(self, input, target, eta, network_optimizer):
loss = self.model._loss(input, target) #首先计算一下前向损失
theta = _concat(self.model.parameters()).data #将所有权重copy一下
try:#替代了optimizer.step() 从而不改变网络权重
moment = _concat(network_optimizer.state[v]['momentum_buffer'] for v in self.model.parameters()).mul_(self.network_momentum)
except:
moment = torch.zeros_like(theta)
'''
带权重衰减和动量的sgd optimizer.step()会使momentum变化
network_optimizer.state[v]['momentum_buffer'] 会变成计算之后的moment
v_{t+1} = mu * v_{t} + g_{t+1} + weight_decay * w 其中weight_decay*w是正则项
w_{t+1} = w_{t} - lr * v_{t+1}
所以:
moment = mu * v_{t}
dw = g_{t+1} + weight_decay * w
v_{t+1} = moment + dw
w'= w - lr * v_{t+1}
'''
dtheta = _concat(torch.autograd.grad(loss, self.model.parameters())).data + self.network_weight_decay*theta
unrolled_model = self._construct_model_from_theta(theta.sub(eta, moment+dtheta))#求w‘
return unrolled_model
def step(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer, unrolled):
# eta是网络的学习率
self.optimizer.zero_grad() #将该batch的alpha的梯度设置为0
if unrolled:#展开要求w‘
self._backward_step_unrolled(input_train, target_train, input_valid, target_valid, eta, network_optimizer)
else: #不展开的话首先将valid计算一次前向传播,再计算损失
self._backward_step(input_valid, target_valid)
self.optimizer.step() #alpha梯度更新
def _backward_step(self, input_valid, target_valid):
loss = self.model._loss(input_valid, target_valid)
loss.backward()
def _backward_step_unrolled(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer):
unrolled_model = self._compute_unrolled_model(input_train, target_train, eta, network_optimizer) #w‘
unrolled_loss = unrolled_model._loss(input_valid, target_valid) #L_val(w')
unrolled_loss.backward() #得到了新的权重
dalpha = [v.grad for v in unrolled_model.arch_parameters()] #dalpha{L_val(w', alpha)}
vector = [v.grad.data for v in unrolled_model.parameters()] #dw'{L_val(w', alpha)}
implicit_grads = self._hessian_vector_product(vector, input_train, target_train)
#更新最后的梯度gradient = dalpha - lr*hessian
for g, ig in zip(dalpha, implicit_grads):
g.data.sub_(eta, ig.data)
for v, g in zip(self.model.arch_parameters(), dalpha):
if v.grad is None:
v.grad = Variable(g.data)
else:
v.grad.data.copy_(g.data)
def _construct_model_from_theta(self, theta):#theta=w'
model_new = self.model.new()
model_dict = self.model.state_dict()
params, offset = {}, 0
for k, v in self.model.named_parameters():
v_length = np.prod(v.size())
params[k] = theta[offset: offset+v_length].view(v.size())
offset += v_length
assert offset == len(theta)
model_dict.update(params)
model_new.load_state_dict(model_dict)
return model_new.cuda()
def _hessian_vector_product(self, vector, input, target, r=1e-2):
R = r / _concat(vector).norm()
# w+ = w + eps*dw'
for p, v in zip(self.model.parameters(), vector):
p.data.add_(R, v)
loss = self.model._loss(input, target)
grads_p = torch.autograd.grad(loss, self.model.arch_parameters())
# w- = w - eps*dw'
for p, v in zip(self.model.parameters(), vector):
p.data.sub_(2*R, v)
loss = self.model._loss(input, target)
grads_n = torch.autograd.grad(loss, self.model.arch_parameters())
for p, v in zip(self.model.parameters(), vector):
p.data.add_(R, v)
return [(x-y).div_(2*R) for x, y in zip(grads_p, grads_n)]
genotypes.py
该函数中只有PRIMITIVES暂时有用,其他的设置可以先不用管。其他的变量是NASNet、AmoebaNet以及DARTS搜索出来的cell结构。
Genotype = namedtuple('Genotype', 'normal normal_concat reduce reduce_concat')
PRIMITIVES = [
'none',
'max_pool_3x3',
'avg_pool_3x3',
'skip_connect',
'sep_conv_3x3',
'sep_conv_5x5',
'dil_conv_3x3',
'dil_conv_5x5'
]
DARTS_V1 = Genotype(normal=[('sep_conv_3x3', 1), ('sep_conv_3x3', 0), ('skip_connect', 0), ('sep_conv_3x3', 1), ('skip_connect', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 0), ('skip_connect', 2)], normal_concat=[2, 3, 4, 5], reduce=[('max_pool_3x3', 0), ('max_pool_3x3', 1), ('skip_connect', 2), ('max_pool_3x3', 0), ('max_pool_3x3', 0), ('skip_connect', 2), ('skip_connect', 2), ('avg_pool_3x3', 0)], reduce_concat=[2, 3, 4, 5])
DARTS_V2 = Genotype(normal=[('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 1), ('skip_connect', 0), ('skip_connect', 0), ('dil_conv_3x3', 2)], normal_concat=[2, 3, 4, 5], reduce=[('max_pool_3x3', 0), ('max_pool_3x3', 1), ('skip_connect', 2), ('max_pool_3x3', 1), ('max_pool_3x3', 0), ('skip_connect', 2), ('skip_connect', 2), ('max_pool_3x3', 1)], reduce_concat=[2, 3, 4, 5])
DARTS = DARTS_V2
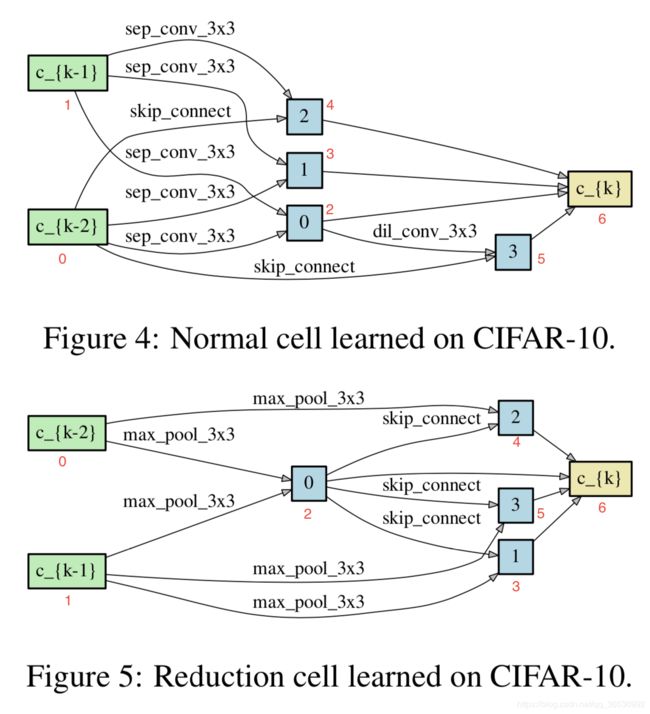
拿DARTS_V2举例来说,nomal代表的是normal cell,reduction代表的是reduction cell(即feature map减小,通道加倍),(‘sep_conv_3x3’, 1)中1代表的上图标红的1,即说明该节点与1相连并且操作是 3 × 3 3\times 3 3×3的深度可分离卷积。
model_search.py
MixedOp
将两节点各种操作实现并加入列表,其中若是pooling,则在后面接上BN
输出则是对各操作的加权相加,所以输入输出维度一样
class MixedOp(nn.Module):
def __init__(self, C, stride):
super(MixedOp, self).__init__()
self._ops = nn.ModuleList()
for primitive in PRIMITIVES:
op = OPS[primitive](C, stride, False)
if 'pool' in primitive:
op = nn.Sequential(op, nn.BatchNorm2d(C, affine=False))
self._ops.append(op)
def forward(self, x, weights):
#weights就是alpha 输出是对各操作的加权相加
return sum(w * op(x) for w, op in zip(weights, self._ops))
Cell
class Cell(nn.Module):
def __init__(self, steps, multiplier, C_prev_prev, C_prev, C, reduction, reduction_prev):
super(Cell, self).__init__()
self.reduction = reduction
if reduction_prev:
self.preprocess0 = FactorizedReduce(C_prev_prev, C, affine=False)
else:
self.preprocess0 = ReLUConvBN(C_prev_prev, C, 1, 1, 0, affine=False)
self.preprocess1 = ReLUConvBN(C_prev, C, 1, 1, 0, affine=False)
self._steps = steps
self._multiplier = multiplier
self._ops = nn.ModuleList()
self._bns = nn.ModuleList()
for i in range(self._steps): # i = 0,1,2,3
for j in range(2+i): # j = 2,3,4,5 因为每处理一个节点,该节点就变为下一个节点的前继
stride = 2 if reduction and j < 2 else 1
op = MixedOp(C, stride) #初始化得到一个节点到另一个节点的操作集合
self._ops.append(op) # len = 14
'''
self._ops[0,1]代表的是内部节点0的前继操作
self._ops[2,3,4]代表的是内部节点1的前继操作
self._ops[5,6,7,8]代表的是内部节点2的前继操作
self._ops[9,10,11,12,13]代表的是内部节点3的前继操作
'''
def forward(self, s0, s1, weights):
s0 = self.preprocess0(s0)
s1 = self.preprocess1(s1)
states = [s0, s1]
offset = 0
for i in range(self._steps):
#因为先将该节点到另一个节点各操作后的输出相加,再把该节点与所有前继节点的操作相加 所以输出维度不变
s = sum(self._ops[offset+j](h, weights[offset+j]) for j, h in enumerate(states))
offset += len(states)
states.append(s)
'''
i=1: s2 = self._ops[0](s0,weights[0]) + self._ops[1](s1,weights[1])即内部节点0
i=2: s3 = self._ops[2](s0,weights[2]) + self._ops[3](s1,weights[3]) + self._ops[4](s2,weights[4])即内部节点1
i=3、4依次计算得到s4,s5
由此可知len(weights)也等于14,因为有8个操作,所以weight[i]有8个值
'''
return torch.cat(states[-self._multiplier:], dim=1) #将后4个节点的输出按channel拼接 channel变为4倍
# eg:(10,3,2,2)+(10,3,2,2)-->(10,6,2,2)
Network(只解析了初始化部分以及genotype部分)
class Network(nn.Module):
def __init__(self, C, num_classes, layers, criterion, steps=4, multiplier=4, stem_multiplier=3):
# c =16 num_class = 10,layers = 8 ,criterion = nn.CrossEntropyLoss().cuda()
super(Network, self).__init__()
self._C = C
self._num_classes = num_classes
self._layers = layers
self._criterion = criterion
self._steps = steps # 4
self._multiplier = multiplier # 4 通道数乘数因子 因为有4个中间节点 代表通道数要扩大4倍
C_curr = stem_multiplier*C # 48
self.stem = nn.Sequential(
nn.Conv2d(3, C_curr, 3, padding=1, bias=False),
nn.BatchNorm2d(C_curr)
)
# 对于第一个cell来说,stem即是s0,也是s1
# C_prev_prev, C_prev是输出channel 48
# C_curr 现在是输入channel 16
C_prev_prev, C_prev, C_curr = C_curr, C_curr, C
self.cells = nn.ModuleList()
reduction_prev = False
for i in range(layers):
# 在 1/3 和 2/3 层减小特征size并且加倍通道.
if i in [layers//3, 2*layers//3]:
C_curr *= 2
reduction = True
else:
reduction = False
cell = Cell(steps, multiplier, C_prev_prev, C_prev, C_curr, reduction, reduction_prev)
reduction_prev = reduction
self.cells += [cell]
C_prev_prev, C_prev = C_prev, multiplier*C_curr
'''
layers = 8, 第2和5个cell是reduction_cell
cells[0]: cell = Cell(4, 4, 48, 48, 16, false, false) 输出[N,16*4,h,w]
cells[1]: cell = Cell(4, 4, 48, 64, 16, false, false) 输出[N,16*4,h,w]
cells[2]: cell = Cell(4, 4, 64, 64, 32, True, false) 输出[N,32*4,h/2,w/2]
cells[3]: cell = Cell(4, 4, 64, 128, 32, false, false) 输出[N,32*4,h/2,w/2]
cells[4]: cell = Cell(4, 4, 128, 128, 32, false, false) 输出[N,32*4,h/2,w/2]
cells[5]: cell = Cell(4, 4, 128, 128, 64, True, false) 输出[N,64*4,h/4,w/4]
cells[6]: cell = Cell(4, 4, 128, 256, 64, false, false) 输出[N,64*4,h/4,w/4]
cells[7]: cell = Cell(4, 4, 256, 256, 64, false, false) 输出[N,64*4,h/4,w/4]
'''
self.global_pooling = nn.AdaptiveAvgPool2d(1)
self.classifier = nn.Linear(C_prev, num_classes)
self._initialize_alphas()
def genotype(self):
def _parse(weights):
# weights [14,8]
gene = []
n = 2
start = 0
for i in range(self._steps):#[0,1,2,3] 代表了中间节点
end = start + n
W = weights[start:end].copy() #获取当前中间节点至前继节点的权重
#sorted返回按alpha降序排列的前继节点的索引
edges = sorted(range(i + 2), key=lambda x: -max(W[x][k] for k in range(len(W[x])) if k != PRIMITIVES.index('none')))[:2]
for j in edges:
k_best = None
for k in range(len(W[j])):# [0~7]
if k != PRIMITIVES.index('none'):
if k_best is None or W[j][k] > W[j][k_best]:
k_best = k #找出与前继节点不包含none的操作中alpha值最大的操作索引
gene.append((PRIMITIVES[k_best], j))
start = end
n += 1
return gene
gene_normal = _parse(F.softmax(self.alphas_normal, dim=-1).data.cpu().numpy()) #按行进行softmax
gene_reduce = _parse(F.softmax(self.alphas_reduce, dim=-1).data.cpu().numpy())
concat = range(2+self._steps-self._multiplier, self._steps+2) # [2,3,4,5]
genotype = Genotype(
normal=gene_normal, normal_concat=concat,
reduce=gene_reduce, reduce_concat=concat
)
return genotype
这里对于为什么要除去none操作,文中给了两点解释

对于第一点比较好理解,但是对于第二点我不是很理解,为什么BN的存在不会影响分类结果以及none操作如何影响节点的结果表示?
train_search.py
def train(train_queue, valid_queue, model, architect, criterion, optimizer, lr):
objs = utils.AvgrageMeter()
top1 = utils.AvgrageMeter()
top5 = utils.AvgrageMeter()
for step, (input, target) in enumerate(train_queue):
model.train()
n = input.size(0)
input = Variable(input, requires_grad=False).cuda()
target = Variable(target, requires_grad=False).cuda(async=True)
# get a random minibatch from the search queue with replacement
input_search, target_search = next(iter(valid_queue))
input_search = Variable(input_search, requires_grad=False).cuda()
target_search = Variable(target_search, requires_grad=False).cuda(async=True)
# 计算并更新alpha的梯度
architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)
optimizer.zero_grad()
logits = model(input)
loss = criterion(logits, target)
loss.backward()
nn.utils.clip_grad_norm(model.parameters(), args.grad_clip) #默认是先求L2正则 控制权重变化不那么大
optimizer.step() #更新网络内部的权重
prec1, prec5 = utils.accuracy(logits, target, topk=(1, 5))
objs.update(loss.data[0], n)
top1.update(prec1.data[0], n)
top5.update(prec5.data[0], n)
if step % args.report_freq == 0:
logging.info('train %03d %e %f %f', step, objs.avg, top1.avg, top5.avg)
return top1.avg, objs.avg
utils.py
drop_path
是dropout的拓展,将运算单元drop的方法应用到路径上,会随机的丢弃一些路径来实现正则化,但是至少保证有一条路径是连接输入和输出的,方法源自于分形网络:
Larsson, Gustav, Michael Maire, and Gregory Shakhnarovich. “Fractalnet: Ultra-deep neural networks without residuals.” arXiv preprint arXiv:1605.07648 (2016).
def drop_path(x, drop_prob):
# 假设x已经是cuda向量
if drop_prob > 0.:
keep_prob = 1.-drop_prob
# bernoulli以keep_prob的概率生成1
# 例如当keep_prob=0.3时,生成的10个数中可能有3个为1
mask = Variable(torch.cuda.FloatTensor(x.size(0), 1, 1, 1).bernoulli_(keep_prob))
# 除以keep_prob是为了让输出预期相同
x.div_(keep_prob)
x.mul_(mask)
return x
关于输出预期相同 cs231n中对dropout做了详细解说,这里简单说明一下,在训练阶段,我们drop了一些神经元,但是在测试阶段,所有神经元都处于活动状态。假设我们以 p p p的概率去保留一些神经元,在训练阶段,一个神经元被丢失后,该神经元预期的输出变为 p ∗ x + ( 1 − p ) ∗ 0 p*x+(1-p)*0 p∗x+(1−p)∗0,因为该神经元的输出有 1 − p 1-p 1−p的概率变为0,所以该神经元的输出预期化简为 p ∗ x p*x p∗x。而测试阶段,所有神经元都处于活动状态,所以该神经元的输出预期就是 x x x,为了让测试阶段和训练阶段输出预期一致,所以在训练阶段,输出必须除以 p p p。