个人项目-数独(Python实现)——从解数独到写游戏
0.项目
项目地址:https://github.com/John-zjm/suduku
GUI地址:https://github.com/John-zjm/sudoku_Gui
1.需求分析
需求分析
1.生成终局 格式:sudoku.exe -c n
1)不重复
2)1<=n<=1000000,能处理非法参数
4)n在1000以内时,要求程序在 60 s 内给出结果
5)输出生成的数独终盘至sudoku.txt
2. 求解数独 格式:sudoku.exe -s path
1)从指定文件读取,每读81个数字视作一道数独题,忽略其他字符
2)要求文件内的数独题目是合法的
3)文件内数独个数在1000以内时,要求程序在 60 s 内给出结果
4)输出已读入数独的答案至sudoku.txt。若存在未满81个的数字,在已解出的答案后输出“存在错误格式!”
2.解题思路
- 我主要把项目分为三部分:
- 输入部分
- 生成数独终局
- 解数独
在写界面的时,只要稍作修改就可以使用后两部分。
详细描述一下这三个部分:
输入略过,有Python的异常处理很好写
生成数独终局用的是行列变换法。数独中间的九宫格经过行列变换可以变换为2!×3!×3!×2!×3!×3!=5184(因为固定左上角为5)。这样我需要生成1000000/5184=192个九宫格就够了,而正中九宫格有8!=40320个足够满足要求。
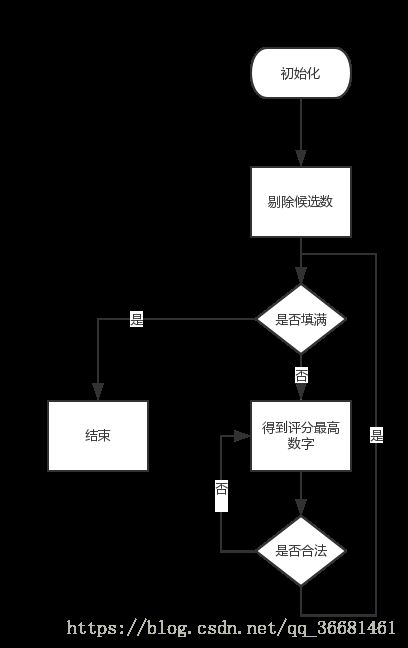
解数独我主要参考了《数独求解的候选数优化算法设计》这篇论文,运用了显性候选数规则、隐性候选数规则、九宫格交叉排除规则。Python的numpy可以很好的对数组进行计算。在进行dfs时,我对候选数进行了估值,具体是(10-候选个数) + 同行确定数字个数 + 同列确实数字个数
3.设计实现
- 输入处理类:
根据参数调用下列函数进行相应处理(包括参数合法性判断) - 终盘生成类:
种子生成函数、交换组合函数、行列交换函数、转换输出函数 - 数独求解类:
初始化函数、记录函数函数、检错函数、恢复函数、深度优先遍历函数、评价函数、减少候选数函数。
sudoku.exe -c 20
sudoku.exe -c 1000000
sudoku.exe -s C:\Users\0\OneDrive\1.txt
sudoku.exe -s C:\
sudoku.exe -p asd“错误数独”
sudo=[[1,2,3,4,5,6,7,8,9]for row in range(9)]
sudo=[[0 for col in range(9)]for row in range(9)]
sudo =[[8,0,0, 0,0,0, 0,0,0]
[0,0,3, 6,0,0, 0,0,0]
[0,7,0, 0,9,0, 2,0,0]
[0,5,0, 0,0,7, 0,0,0]
[0,0,0, 0,4,5, 7,0,0]
[0,0,0, 1,0,0, 0,3,0]
[0,0,1, 0,0,0, 0,6,8]
[0,0,8, 5,0,0, 0,1,0]
[0,9,0, 0,0,0, 4,0,0]]4.性能改进
- 把输出改为一次输出,输入改为一次读入,多次处理。
- 在回溯时,用估值函数,让价值大的候选数先进循环
- 在界面中,把检测数独从全部检测,改为对修改数的所在行,所在列,所在九宫格进行检测。
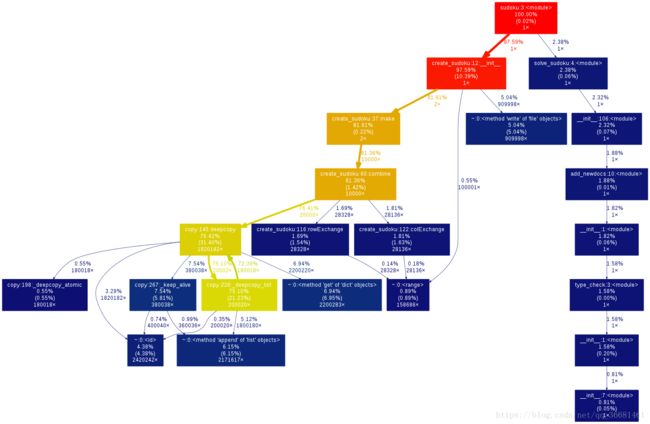

由图可以看出combine()和check_one_possible()消耗较大
def combine(self, c1, c2, c3, r1, r2, r3):
self.table = deepcopy(self.temp)
if (c1 == 1):
self.colExchange(1, 2)
if (c2 == 1):
self.colExchange(4, 5)
if (c2 == 2):
self.colExchange(3, 4)
if (c2 == 3):
self.colExchange(3, 4)
self.colExchange(4, 5)
if (c2 == 4):
self.colExchange(3, 5)
self.colExchange(4, 5)
if (c2 == 5):
self.colExchange(3, 5)
if (c3 == 1):
self.colExchange(7, 8)
if (c3 == 2):
self.colExchange(6, 7)
if (c3 == 3):
self.colExchange(6, 7)
self.colExchange(7, 8)
if (c3 == 4):
self.colExchange(6, 8)
self.colExchange(7, 8)
if (c3 == 5):
self.colExchange(6, 8)
if (r1 == 1):
self.rowExchange(1, 2)
if (r2 == 1):
self.rowExchange(4, 5)
if (r2 == 2):
self.rowExchange(3, 4)
if (r2 == 3):
self.rowExchange(3, 4)
self.rowExchange(4, 5)
if (r2 == 4):
self.rowExchange(3, 5)
self.rowExchange(4, 5)
if (r2 == 5):
self.rowExchange(3, 5)
if (r3 == 1):
self.rowExchange(7, 8)
if (r3 == 2):
self.rowExchange(6, 7)
if (r3 == 3):
self.rowExchange(6, 7)
self.rowExchange(7, 8)
if (r3 == 4):
self.rowExchange(6, 8)
self.rowExchange(7, 8)
if (r3 == 5):
self.rowExchange(6, 8)
self.sudoku_map.append(deepcopy(self.table))# 显性候选数
def _check_one_possbile(self):
# 同一行只有一个数字的情况
for r in range(0, 9):
values = filter(lambda x: isinstance(x, list), self.value[r])
for c, item in enumerate(self.value[r]):
if isinstance(item, list):
for value in item:
if sum(map(lambda x: x.count(value), values)) == 1:
self.value[r, c] = value
self.new_points.put((r, c))
return True
# 同一列只有一个数字的情况
for c in range(0, 9):
values = filter(lambda x: isinstance(x, list), self.value[:, c])
for r, item in enumerate(self.value[:, c]):
if isinstance(item, list):
for value in item:
if sum(map(lambda x: x.count(value), values)) == 1:
self.value[r, c] = value
self.new_points.put((r, c))
return True
# 九宫格内的单元格只有一个数字的情况
for r, c in self.base_points:
values = filter(lambda x: isinstance(x, list),
self.value[r:r+3, c:c+3].reshape(1, -1)[0])
for m_r, row in enumerate(self.value[r:r+3, c:c+3]):
for m_c, item in enumerate(row):
if isinstance(item, list):
for value in item:
if sum(map(lambda x: x.count(value), values)) == 1:
self.value[r+m_r, c+m_c] = value
self.new_points.put((r+m_r, c+m_c))
return True5.代码说明
# 找到下一个全排列
i = len(sudo_num)-2
while i >= 0 and sudo_num[i] >= sudo_num[i+1]:
i -= 1
j = i + 1
k = len(sudo_num) - 1
while sudo_num[i] >= sudo_num[k]:
k -= 1
(sudo_num[i], sudo_num[k]) = (sudo_num[k], sudo_num[i])
sudo_num[j:] = sudo_num[:j-1:-1]这部分属于生成数独,主要对九宫格进行变换,生成下一个非递增的全排列,以实现变换中心九宫格。
# 九宫格交叉排除规则
def _check_same_num(self):
for b_r, b_c in self.base_points:
block = self.value[b_r:b_r+3, b_c:b_c+3]
# 判断数字1~9在该九宫格的分布情况
data = block.reshape(1, -1)[0]
for i in range(1, 10):
result = map(lambda x: 0 if not isinstance(
x[1], list) else x[0] + 1 if x[1].count(i) else 0, enumerate(data))
result = filter(lambda x: x > 0, result)
r_count = len(result)
if r_count in [2, 3]:
# 2或3个元素才有可能同一行或同一列
rows = map(lambda x: (x-1) / 3, result)
cols = map(lambda x: (x-1) % 3, result)
if len(set(rows)) == 1:
# 同一行,去掉其他行的数字
result = map(lambda x: b_c + (x-1) % 3, result)
row = b_r + rows[0]
for col in range(0, 9):
if col not in result:
item = self.value[row, col]
if isinstance(item, list):
if item.count(i):
item.remove(i)
# 判断移除后,是否剩下一个元素
if len(item) == 1:
self.new_points.put((row, col))
self.value[row, col] = item[0]
return True
elif len(set(cols)) == 1:
# 同一列
result = map(lambda x: b_r + (x-1)/3, result)
col = b_c + cols[0]
for row in range(0, 9):
if row not in result:
item = self.value[row, col]
if isinstance(item, list):
if item.count(i):
item.remove(i)
# 判断移除后,是否剩下一个元素
if len(item) == 1:
self.new_points.put((row, col))
self.value[row, col] = item[0]
return True这部分属于解决数独。为九宫格交叉排除规则。(九宫格交叉排除规则) 若同一个九 宫格里,某个数字 x 仅出现在格子 d1, d2,…, dn (2 ≤n ≤ 3) 的候选数集合 ω1, ω2,…, ωn 中,且 d1, d2,…, dn 是在同一行(或列),那么同一行(或列) 的其他未填入数字格子d1, d2,…, dm(1 ≤ m ≤9 - n) 候选数集合 ω’1, ω’ 2,…, ω’m可以将数字x排除。
如图
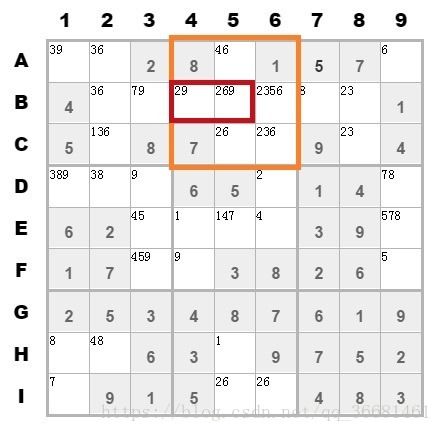
在图中,第二个九宫格中的B行出现了2,9两次。则B8可以排除2,B3可以排除9。
while True:
self.dig_hole()
if (self.hoels > 30):
if (self.lev > level*30): # 猜测次数0~30位简单,30~60为中等,60~无穷为困难
break
if self.hoels > 30+level*10: # 30~40空为简单 40~50为中等 50~60为困难
break这部分属于生成数独游戏,根据解数独的猜测次数来判断,如果猜测次数小于30或空为40个,则为简单。以此类推。
def check_value(self, row, col):
b_r = int(row/3)*3
b_c = int(col/3)*3
# 行
for i in range(1, 10):
sum = 0
record = -1
for j in range(9):
if self.map[row][j] == i:
sum = sum + 1
if sum == 1:
record = j # 有一个
elif sum == 2: # 有两个重复数字
if self.isyuan[row][record] != 1: # 是否为题目数字
self.heng_base[row][record] = 1
self.show_num[row][record].setStyleSheet(
"background-color: red;")
record = -1
if self.isyuan[row][j] != 1:
self.heng_base[row][j] = 1
self.show_num[row][j].setStyleSheet(
"background-color: red;")
elif sum > 2: # 有更多
if self.isyuan[row][j] != 1:
self.heng_base[row][j] = 1
self.show_num[row][j].setStyleSheet(
"background-color: red;")
if (record != -1): # 无重复
self.heng_base[row][record] = 0
# 在其他方面没有错误
if (self.shu_base[row][record] == 0) & (self.kuai_base[row][record] == 0):
if self.isyuan[row][record] != 1:
self.show_num[row][record].setStyleSheet(
"background-color: green;")
# 列
for i in range(1, 10):
sum = 0
record = -1
for j in range(9):
if self.map[j][col] == i:
sum = sum + 1
if sum == 1:
record = j
elif sum == 2:
if self.isyuan[record][col] != 1:
self.shu_base[record][col] = 1
self.show_num[record][col].setStyleSheet(
"background-color: red;")
record = -1
if self.isyuan[j][col] != 1:
self.shu_base[j][col] = 1
self.show_num[j][col].setStyleSheet(
"background-color: red;")
elif sum > 2:
if self.isyuan[j][col] != 1:
self.shu_base[j][col] = 1
self.show_num[j][col].setStyleSheet(
"background-color: red;")
if (record != -1):
self.shu_base[record][col] = 0
if (self.heng_base[record][col] == 0) & (self.kuai_base[record][col] == 0):
if self.isyuan[record][col] != 1:
self.show_num[record][col].setStyleSheet(
"background-color: green;")
# 九宫格
for i in range(1, 10):
sum = 0
record = [-1, -1]
for jrow in range(3):
for jcol in range(3):
if self.map[jrow+b_r][jcol+b_c] == i:
sum = sum + 1
if sum == 1:
record = [jrow+b_r, jcol+b_c]
elif sum == 2:
if self.isyuan[record[0]][record[1]] != 1:
self.kuai_base[record[0]][record[1]] = 1
self.show_num[record[0]][record[1]].setStyleSheet(
"background-color: red;")
record = [-1, -1]
if self.isyuan[jrow+b_r][jcol + b_c] != 1:
self.kuai_base[jrow+b_r][jcol + b_c] = 1
self.show_num[jrow+b_r][jcol +
b_c].setStyleSheet("background-color: red;")
elif sum > 2:
if self.isyuan[jrow+b_r][jcol + b_c] != 1:
self.kuai_base[jrow + b_r][jcol + b_c] = 1
self.show_num[jrow+b_r][jcol +
b_c].setStyleSheet("background-color: red;")
if (record[0] != -1):
self.kuai_base[record[0]][record[1]] = 0
if(self.heng_base[record[0]][record[1]] == 0) & (self.shu_base[record[0]][record[1]] == 0):
if self.isyuan[record[0]][record[1]] != 1:
self.show_num[record[0]][record[1]].setStyleSheet(
"background-color: green;")这部分为界面部分。主要为动态的显示填入数字的对错。如果是对的则是绿色,如果是错的,则是红色。



6.总结
这次的项目,第一部分完成的较快,没有出现太大的问题。但在附加题部分,我因为对qt的信号不熟练,导致出了很多Bug,耽误了很多时间。总体来说,这个项目使我的python有了一个提高。