Gabor变换过程详细推导
写在前面
强烈建议阅读博文 matlab学习:图像频域分析之Gabor滤波,该篇博文写的非常好,由浅入深,对于Gabor滤波的由来及优点等叙述的非常完善。在本篇中,将集中于公式的推导。
一维情况
在传统的傅里叶变换中:
F ( j ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t \ F(j\omega)=\int_{ - \infty }^\infty f (t){e^{ - j\omega t}}dt\, F(jω)=∫−∞∞f(t)e−jωtdt
相应的逆变换为:
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e j ω t d ω \ f(t) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty F (\omega){e^{j\omega t}}d\omega\, f(t)=2π1∫−∞∞F(ω)ejωtdω
傅里叶变换只能反映整体的频率特性,无法获得某一时刻的频率响应,我们无法将时域频域结合起来进行分析。为此,我们可以对原始函数加窗,即为窗口傅里叶变换,也为Gabor变换。
一维Gabor核
令原始函数 f ∈ L 2 ( R ) f \in {L^2}(R) f∈L2(R),则加窗傅里叶变换为:
G f ( a ; b , ω ) = ∫ − ∞ ∞ f ( t ) g a ( t − b ) e − j ω t d t \ {G_f}(a;b,\omega ) = \int_{ - \infty }^\infty f (t)g_a^{}(t - b){e^{ - j\omega t}}dt\, Gf(a;b,ω)=∫−∞∞f(t)ga(t−b)e−jωtdt
其中, g a ( t ) = 1 2 π a exp ( − t 2 4 a ) \ {g_a}(t) = \frac{1}{{2\sqrt {\pi a} }}\exp \left( { - \frac{{{t^2}}}{{4a}}} \right) ga(t)=2πa1exp(−4at2)为高斯窗函数,其中 a > 0 , b > 0 a>0,b>0 a>0,b>0,参数 b b b用于平行移动窗口,以便于覆盖整个时域。
在上式中, G f ( a ; b , ω ) {G_f}(a;b,\omega ) Gf(a;b,ω)也可看做 f ( t ) f(t) f(t)和 h ( t ) = g a ( t − b ) e j ω t h(t)=g_a^{}(t - b){e^{ j\omega t}} h(t)=ga(t−b)ejωt的卷积,即
G f ( a ; b , ω ) = Γ ( f ( t ) ∗ h ( t ) ) {G_f}(a;b,\omega )= \Gamma(f(t)*h(t)) Gf(a;b,ω)=Γ(f(t)∗h(t))
此时,假设 b = 0 b=0 b=0, g a ( t ) = 1 2 π a exp ( − t 2 4 a ) {g_a}(t) = \frac{1}{{2\sqrt {\pi a} }}\exp \left( { - \frac{{{t^2}}}{{4a}}} \right) ga(t)=2πa1exp(−4at2),为了便于计算,令 T = 4 a T=4a T=4a,当 , ω = ω 0 ,\omega=\omega _0 ,ω=ω0时,
h ( t ) = 1 π T e − t 2 T e j ω 0 t h(t) =\frac{1}{{\sqrt {\pi T} }}{e^{ - \frac{{{t^2}}}{T}}}{e^{j{\omega _0}t}}\, h(t)=πT1e−Tt2ejω0t
其傅里叶变换为:
H ( ω ) = 1 T e − T ( ω − ω 0 ) 2 / 4 \ H(\omega ) = \frac{1}{T}{e^{ - T{{(\omega - {\omega _0})}^2}/4}}\, H(ω)=T1e−T(ω−ω0)2/4
公式中可以看出,其中心频率为 ω 0 \omega_0 ω0,带宽为 4 / T \sqrt{4/T} 4/T.并且可以看出,时域窗口固定时,频域 H ( ω ) H(\omega ) H(ω)的带宽是不变的。在实际应用中,频率越高,带宽应该越小。这也是Gabor变换的一个局限。
二维Gabor核
我们可以将滤波核的维度从一维拓展到二维,同理二维中
h ( x , y ) = g ( x ′ , y ′ ) exp [ 2 π j ( U x + V y ) ] \ h(x,y) = g\left( {{x^\prime },{y^\prime }} \right)\exp [2\pi j(Ux + Vy)]\, h(x,y)=g(x′,y′)exp[2πj(Ux+Vy)]
式中 ( U , V ) (U,V) (U,V)表示特定的空间频率, g ( x ′ , y ′ ) g\left( {{x^\prime },{y^\prime }} \right) g(x′,y′)为下式所示的高斯函数。
g ( x ′ , y ′ ) = 1 2 π σ 2 exp [ − x ′ 2 + y ′ 2 2 σ 2 ] \ g\left( {{x^\prime },{y^\prime }} \right) = \frac{1}{{2\pi {\sigma ^2}}}\exp \left[ { - \frac{{{x^\prime }^2 + {y^\prime }^2}}{{2{\sigma ^2}}}} \right]\, g(x′,y′)=2πσ21exp[−2σ2x′2+y′2]
( x ′ , y ′ ) = ( x cos ( θ ) + y sin ( θ ) , − x sin ( θ ) + y cos ( θ ) ) \ \left( {{x^\prime },{y^\prime }} \right) = (x\cos (\theta ) + y\sin (\theta ), - x\sin (\theta ) + y\cos (\theta ))\, (x′,y′)=(xcos(θ)+ysin(θ),−xsin(θ)+ycos(θ))
h ( x , y ) h(x,y) h(x,y)的傅里叶变换为
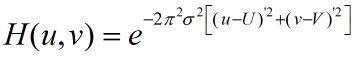
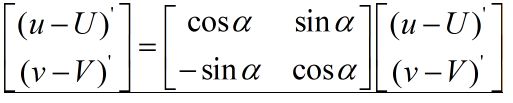
当然,在实际的应用中,考虑的因素更多,这里大家可以参考 Gabor滤波器学习。
[1]:https://www.cnblogs.com/yingying0907/archive/2012/11/22/2781945.html
[2]: https://blog.csdn.net/jinshengtao/article/details/17797641
[3]: 贾朱植, 董立文, 董勃, 谢元旦, JIA Zhu-zhi, DONG Li-wen, DONG Bo, XIE Yuan-dan - 《鞍山科技大学学报》 2005年1期