Codeforces Round #514 (Div. 2)

A了两道题，第三题没看懂，第五题没看完，第四题还没来得及看。 

Codeforces Round #514 (Div. 2)

A. Cashier 

#include
#include
using namespace std;

int main(){
	int n,L,a,pre=0,t,l;
	int cnt=0;
	scanf("%d%d%d",&n,&L,&a);
	while(n--){
		scanf("%d%d",&t,&l);
		cnt+=(t-pre)/a;
		pre=t+l;
	}
	cnt+=(L-pre)/a;
	printf("%d\n",cnt);
	return 0;
} 

 

B. Forgery 

姑且就把这题理解成盖印章，问印章能否印出下面的图案？枚举中心点，判断其合理性。合理的话给八个方向的'#'做上标记，说明能够盖出这8个'#'。最后枚举所有的'#'，看这些’#‘是否都能盖出。

#include
#include
#include
using namespace std;

const int maxn=1010;
char mp[maxn][maxn];
bool flag[maxn][maxn];
int dir[8][2]={-1,-1,-1,0,-1,1,0,-1,0,1,1,-1,1,0,1,1};
int n,m;

bool check(int x,int y){      //枚举可能是中心点的点，判断这个点是中心点是否合理
	for(int i=0;i<8;i++){
		int fx=x+dir[i][0],fy=y+dir[i][1];
		if(mp[fx][fy]=='.') return false;
	}
	return true;
}

void change(int x,int y){   //合理的话，修改周边'#'的标记，说明这个'#'能被写出
	for(int i=0;i<8;i++){
		int fx=x+dir[i][0],fy=y+dir[i][1];
		flag[fx][fy]=true;
	}
}

bool work(){   //枚举所有点，如果有'#'没被写出，说明这个图形不合法，不能伪造出来
	for(int i=0;i

 

 C. Sequence Transformation

题目大意：给你一个集合A，元素是1-n，找出集合A中所有元素的最大公约数x。将x放进集合B中，从集合A中移除一个元素（这个元素是任意的）；继续重复这个过程，直到集合A为空。输出依次放入集合B的这n个数——输出序列。问输出序列字典序的最大值。也就是如何移除数，才能使得最大公约数增大？

题解：尽快得使最大公约数增大，也就是消去1，3，5，7，9……（还剩2,4,6,8,10……）这时最大公约数为2

消去2，6，10……（还剩4,8……） 这时最大公约数为4

每次都是从剩下的序列中隔一个消一个，如果序列还剩三个数的话，肯定能提取成t*（1,2,3）这种形式---->t*(1,1,3).

1.递推写法

#include
#include
using namespace std;

int main() {
	int n;
    scanf("%d",&n);
    int res=1,cnt=n,len;
    for(int i=0;(1<

2.递归写法 

#include
#include
#include
using namespace std;

void func(int s, int t)
{
	if(s==0) return;
	if(s==3)
	{
		printf("%d %d %d",t,t,3*t);
		return;
	}
	int cnt = 0;
	for(int i=1;i<=s;i+=2) cnt++,printf("%d ",t);
	func(s-cnt,t*2);
}

int main(){
	int a;
	scanf("%d",&a);
	func(a,1);
	return 0;
}

 

D. Nature Reserve 

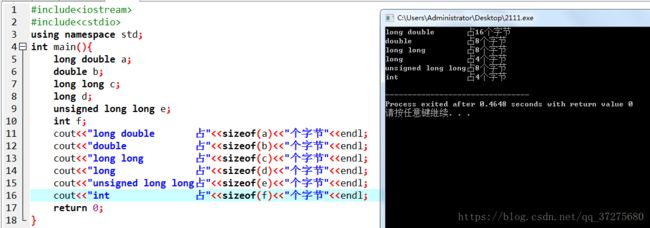
题解：long double 的范围要比double的广，因此使用long double 精度要更高些。

一些常用数据类型的长度入下

涉及的代码：

#include
#include
using namespace std;
int main(){
	long double a;
	double b;
	long long c;
	long d;
	unsigned long long e;
	int f;
	cout<<"long double       占"<

 

---

 

 E. Split the Tree

题解：有一个以1为根节点的树，问你将树至少分成几部分，才能使得每部分的节点个数不超过L个，并且权值之和不超过S?（每部分都是一条路径，后一节点是前个节点的父亲，A vertical path is a sequence of vertices v1,v2,…,vk where vi (i≥2) is the parent of vi−1.）

我的做法就是自下向上找父亲，如果满足这条路径上节点不超过L个，权值之和不超过S，继续往上找。知道找到不满足条件的，它可能需要开辟一条新的路径。

#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
ll w[maxn];
ll fa[maxn];
bool flag[maxn];

int main(){
	ll n,L;
	ll S;
	scanf("%lld%lld%lld",&n,&L,&S);
	bool tag=true;
	for(ll i=1;i<=n;i++){
		scanf("%lld",&w[i]);
		if(w[i]>S) tag=false;
	}
	
	for(ll i=2;i<=n;i++){
		scanf("%lld",&fa[i]);
	}
	
	if(!tag){
		printf("-1\n");
		return 0;
	}
	ll ans=0,tl,ts,tmp;
	for(ll i=n;i>=1;i--){
		if(!flag[i]){
			ans++;
			tl=L;
			ts=S;
			tmp=i;
			while(ts>=w[tmp]&&tl&&tmp){
				tl--;
				ts=ts-w[tmp];
				flag[tmp]=true;
				tmp=fa[tmp];
			}
		}
	}
	printf("%lld\n",ans);
	return 0;
}