神经网络训练加速、增加稀疏性操作（Dropout、GN、BN、LRN）

增加稀疏性（降低过拟合风险）----Dropout、LRN

Dropout

        Dropout是怎么做到防止过拟合的呢？首先，想象我们现在只训练一个特定的网络，当迭代次数增多的时候，可能出现网络对训练集拟合的很好，但是对验证集的拟合程度很差的情况。所以，我们有了这样的想法：可不可以让每迭代随机的去更新网络参数，引入这样的随机性就可以增加网络generalize 的能力。所以就有了dropout 。

        Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征，如图所示。

                                                             

Dropout工作流程：

假设我们要训练这样一个神经网络，如左侧图所示。然后，输入是x输出是y，正常的流程是：我们首先把x通过网络前向传播，然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后，过程变成如下：

(1) 首先随机（临时）删掉网络中一半的隐藏神经元，输入输出神经元保持不变（右侧图中虚线为部分临时被删除的神经元）

(2) 然后把输入x通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）。

(3) 然后继续重复这一过程：恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）。从隐藏层神经元中随机选择一个一半大小的子集临时删除掉（备份被删除神经元的参数）对一小批训练样本，先前向传播然后反向传播损失并根据随机梯度下降法更新参数（w，b）。

                                                            

局部响应归一化（Local Response Normalization，LRN）

        LRN层模仿了生物神经系统的“侧抑制”机制，LRN层对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。LRN函数类似DROPOUT和数据增强，通常作为relu激励之后防止数据过拟合而提出的一种处理方法。这个函数很少使用，基本上被类似DROPOUT这样的方法取代，见最早的出处AlexNet论文对它的定义, 《ImageNet Classification with Deep Convolutional Neural Networks》

        LRN对于ReLU这种没有上限边界的激活函数会比较有用，因为它会从附近的多个卷积核的响应中挑选比较大的反馈，但不适合Sigmoid之中有固定边界并且能抑制过大值的激活函数。 其公式如下：

                                                             

        ai表示第i个核在位置（x,y）运用激活函数ReLU后的输出，n是同一位置上临近的kernal map的数目（由此看出该方法是按照通道维度进行计算的），N是kernal的总数。参数K,n,alpha，belta都是超参数，一般设置k=2,n=5,aloha=1*e-4,beta=0.75。b为归一化结果。

       总的来说，上述公式是输入除以一个系数来达到归一化的目的，公式的核心在于该系数的计算，该系数的意义是不同通道（feature map）的累加平方和。（n、N、α、β为已知参数）

神经网络训练加速----BN、GN

Batch  Normalization

        BN是有启发来源的：之前的研究表明如果在图像处理中对输入图像进行白化（Whiten）操作的话——所谓白化，就是对输入数据分布变换到0均值，单位方差的正态分布——那么神经网络会较快收敛，那么BN作者就开始推论了：图像是深度神经网络的输入层，做白化能加快收敛，那么其实对于深度网络来说，其中某个隐层的神经元是下一层的输入，意思是其实深度神经网络的每一个隐层都是输入层，不过是相对下一层来说而已，那么能不能对每个隐层都做白化呢？这就是启发BN产生的原初想法，而BN也确实就是这么做的，可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作。

        BN的基本思想其实相当直观：因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

Group Normalization

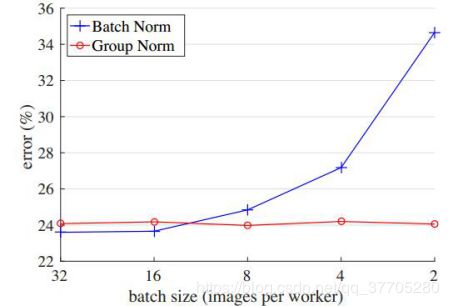
       Group Normalization（GN）是针对Batch Normalization（BN）在batch size较小时错误率较高而提出的改进算法，因为BN层的计算结果依赖当前batch的数据，当batch size较小时（比如2、4这样），该batch数据的均值和方差的代表性较差，因此对最后的结果影响也较大。从下图中我们可以看出BN与GN的性能对比，随着Batch减小，GN显现出优势。

                                        

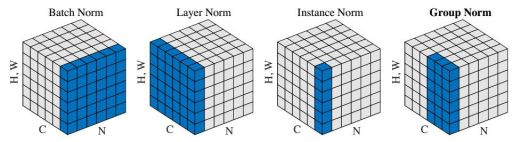
各种正则化之间的区别，如下图所示：

                            

上图中N代表Batch维度，C代表通道维度，（H，W）可以看作是一张feature map展成的一维数据。

      （1） BatchNorm：在batch方向做归一化（即不同图片的相同通道之间做归一化），计算N*H*W的均值  

      （2）GroupNorm：将channel方向分group，然后每个group内做归一化，算(C//G)*H*W的均值，下面的两种都可以看作是GN的而特殊情况（一个G为c，一个G为1）

      （3）LayerNorm：在channel方向做归一化（也就是卷积的某一个层），算C*H*W的均值

      （4）InstanceNorm：一个channel内做归一化，算H*W的均值

GN工作原理：

        在深度学习没有火起来之前，提取特征通常是使用SIFT，HOG和GIST特征，这些特征有一个共性，都具有按group表示的特性，每一个group由相同种类直方图的构建而成，这些特征通常是对在每个直方图（histogram）或每个方向（orientation）上进行组归一化（group-wise norm）而得到。而更高维的特征比如VLAD和Fisher Vectors(FV)也可以看作是group-wise feature，此处的group可以被认为是每个聚类（cluster）下的子向量sub-vector。

        从深度学习上来讲，完全可以认为卷积提取的特征是一种非结构化的特征或者向量，拿网络的第一层卷积为例，卷积层中的的卷积核filter1和此卷积核的其他经过transform过的版本filter2（transform可以是horizontal flipping等），在同一张图像上学习到的特征应该是具有相同的分布，那么，具有相同的特征可以被分到同一个group中，按照个人理解，每一层有很多的卷积核，这些核学习到的特征并不完全是独立的，某些特征具有相同的分布，因此可以被group。

       导致分组（group）的因素有很多，比如频率、形状、亮度和纹理等，HOG特征根据orientation分组，而对神经网络来讲，其提取特征的机制更加复杂，也更加难以描述，变得不那么直观。另在神经科学领域，一种被广泛接受的计算模型是对cell的响应做归一化，此现象存在于浅层视觉皮层和整个视觉系统。

       作者基于此，提出了组归一化（Group Normalization）的方式，且效果表明，显著优于BN、LN、IN等。GN的归一化方式避开了batch size对模型的影响，特征的group归一化同样可以解决Internal Covariate Shift 的问题，并取得较好的效果。

 

参考文章：

GN：

https://zhuanlan.zhihu.com/p/55739361

https://www.cnblogs.com/yumoye/p/11358624.html