算法:最短路算法

计算最短路的三大算法

常见计算最短路的题型模板:输入n代表结点数，输入m代表边数，接下来m行，每行三个数，分别输入n1,n2,k代表结点n1到结点n2的单向路径长度为k

1. Floyd算法模板
   基于动态规划思想，核心在于，为了计算两个结点i,j之间的最短路，需要引入中转结点k进行进一步比较，来对领接矩阵进行进一步更新,状态转移方程为map[i][j]=min(map[i][k]+map[k][j],map[i][j])
   

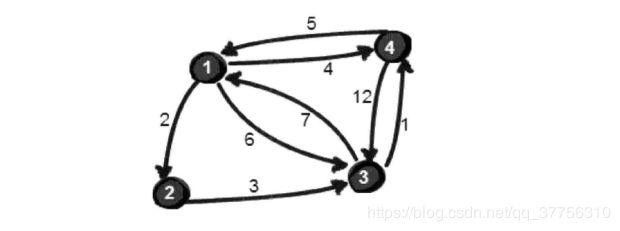
//我们假设结点的范围为1~n
//领接矩阵map[i][j]代表结点i到j的初始距离
for(i in (1 to n))
	for(j in (1 to n))
		map[i][j] = min(map[i][1],map[1][j];
		//此处尝试以第1个结点进行中转结点进行更新		

for(i in (1 to n))
	for(j in (1 to n))
		map[i][j] = min(map[i][2],map[2][j];
		//此处尝试以第2个结点进行中转结点进行更新		

for(i in (1 to n))
	for(j in (1 to n))
		map[i][j] = min(map[i][3],map[3][j];
		//此处尝试以第3个结点进行中转结点进行更新	
.....
以下略过
.....			
for(i in (1 to n))
	for(j in (1 to n))
		map[i][j] = min(map[i][n],map[n][j];
		//此处尝试以第n个结点进行中转结点进行更新	

不难看出，我们要引入n次中转结点，整个算法时间复杂度是O(n^3),效率有点低，适合数据量不大的情况下快速使用，java代码如下

	static void foyed(int[][] map) {
	//加载领接矩阵
		int len = map.length;
		for(int k = 1;k

2. Dijikstra算法模板
   同样是基于动态规划思想，相比于floyd算法，Dijikstra算法就相对效率高些，此算法可以计算出某个结点分别到其他所有结点之间的最短路径，我们只需要额外建两个数组，数组1假设名字为dis[]，用来存储初始结点到其他结点之间的距离，数组2，假设名字为book[]，用来判断结点是否已经被访问，在一步步迭代中，只需要对这个标记数组进行更新，最终就可以求出初始点到其他结点之间的最短距离
   
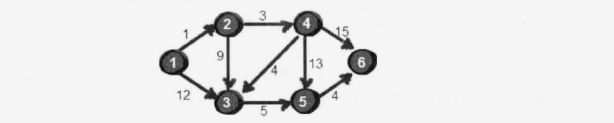
   例如，求结点1到分别到其他所有结点之间的最短距离的整个过程 1.加载领接矩阵map 2.新建一个dis[]数组，长度为结点的数量，初始化dis数组元素，使得dis中下标为i的元素值为结点1到结点i的距离 3.新建一个book[]数组，除第一项初始化为1之外(因为第一项是起点，初始时已经默认开始加入访问状态集合)，其他都初始化为0(其他结点还没有开始访问) 4.开始更新dis[]数组 5.dis[]数组更新完毕
   上code

//Dijikstra算法
	//需要两个数组dis和book,dis用来更新初始结点到其他结点之间的距离，book结点用来标记结点是否已经访问
	static void Dijkstra(int[][] map,int[] book,int begin) {//加载领接矩阵，book数组，初始结点
		int[] dis = new int[map.length];
		int len = map.length;
		//初始化dis数组
		for(int i=1;i

3. BF算法模板
   dijistra算法优化后虽然强大，但是他对于决负权边的存在就无计可施了，下面这个BF算法就很牛逼了，既能解决floyd的时间复杂度问题，还可以解决负权边存在的问题，并且经过队列的优化，可以进一步提升算法的健壮性，这里我简单总结一下过程

如上图所示，在这里依然要使用一个dis数组，存储初始结点到其余各个结点的初始距离，以上图为例，dis[]数组第一步就将初始化为dis[] = {0,-3,N,N,5} (N表示无穷大)，接下来，对于结点1与结点2，与它们之间的路径长度这三种变量，我们要分别使用三个数组存储，分别是begin[],end[]和distance[]数组，使用一个循环依次遍历每一行输入的数据，分别将它们存储到着三个数组中去，接下来我们分成每一步进行计算
第一步时的dis数组已经初始化完成，为[0,-3,N,N,5]
第二步，我们开始第一轮遍历，对于每一行的三个数据begin[i],end[i],distance[i],我们看看dis[end[i]]是否要大于dis[begin[i]]+distance[i],如果大于，则需要更新，状态转移方程为dis[end[i]] = min(dis[end[i]],dis[begin[i]]+distance[i])，第一轮过后的数组更新情况为[0,-3,-1,2,5]
第三步，我们进行第二轮遍历，此时dis更新为[0,-3,-1,2,4]
…
由于在一个含有n个顶点的图中，任何两个结点之间的最短路径数都是n-1所以，我们只需要遍历n-1次即可
最终代码如下:

import java.util.Arrays;
import java.util.Scanner;

public class Bellman算法 {
	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		int city = in.nextInt();//城市数目
		int num = in.nextInt();//边的数目
		int[] dis = new int[city+1];
		for(int i=1;i<=city;i++) {
			dis[i] = 100000;//初始化一个极大值，注意不要过大
		}
		dis[1] = 0;
		int[] begin = new int[num+1];
		int[] end = new int[num+1];
		int distance[] = new int[num+1];
		for(int i=1;i<=num;i++) {
			begin[i] = in.nextInt();//起点
			end[i] = in.nextInt();//终点
			distance[i] = in.nextInt();//起点到终点的距离
		}
		int[] ans = getMiniPath(dis, begin, end, distance);
		for(int i=1;i<=city;i++) {
			System.out.println(dis[i]);//输出dis
		}
	}
	
	static int[] getMiniPath(int[] dis,int[] begin,int[] end,int[] distance) {
		int city = dis.length-1;
		int path = distance.length-1;
		int[] dis_ = dis;
		for(int i=1;i

任重而道远～