洛谷题解(持续更新)
洛谷题解(持续更新)
文章目录
- 洛谷题解(持续更新)
- P1067 多项式输出
- P1540 机器翻译
- P1563 玩具谜题
- P1031均分纸牌
- P1098 字符串的展开
P1067 多项式输出

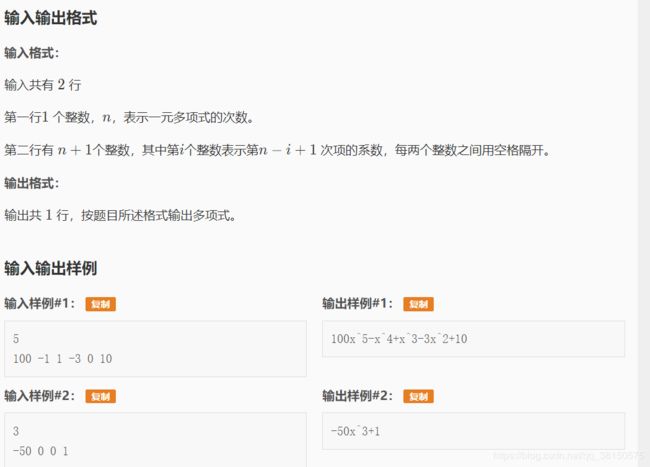
思路:本题没有难度系数,但是需要把所有情况考虑到。我是按照指数分类,再对系数的不同情况进行讨论。基本分为 -1, 0, 1 三个点段。
1.指数为 0 :根据是否为第一个出现的项决定+,其余情况只输出系数。
2.指数为1:根据是否为第一个出现的项决定+,其余情况根据系数是否为1输出X或系数和X的组合。
3.指数大于1:根据是否为第一个出现的项决定+,其余情况根据系数是否为1输出X^ 的i次组合或系数和X^的i次组合。
#include
#include
using namespace std;
int main()
{
int number[113], n, flag =1;
cin>>n;
for(int i = n; i>=0; i--)
{
cin>>number[ i ];
}
for(int i = n; i>=0; i--)
{
if(i == 0)
{
if(number[i]>0&&!flag)
cout<<"+"<1 && flag) ||number[i]<-1 )
{
cout<1 && !flag)
{
cout<<"+"<1 && flag) ||number[i]<-1 )
{
cout<1 && !flag)
{
cout<<"+"< P1540 机器翻译
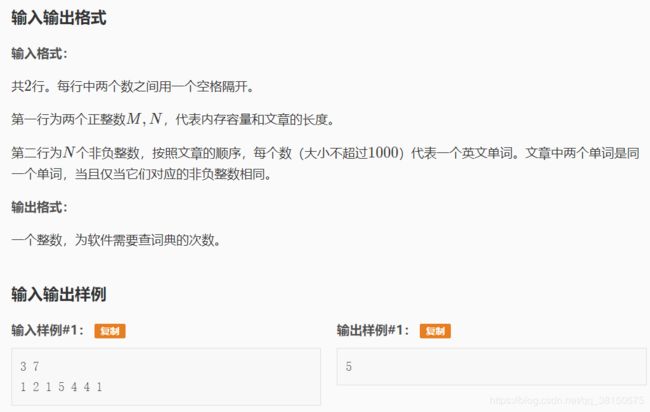
思路:本题考察的是先进先出的思想,可以使用队列链表等数据结构解出。这个也是成FIFO内存置换算法的思想。由于数据量不大,我采用的是数组形式。
1.定义内存数组和数据数组。
2.每次遍历读入数据,比较是否在内存中。通过first变量的变换确定每一次置换的位置。记录置换次数
3.输出结果。
#include
#include
#include
#define Max_size 1100
using namespace std ;
int main()
{
int array[ Max_size ], store[120], number = 0;
int M, N, flag = 1, first = 0; //flag表示是否找到这个数据
cin>>M>>N;
for(int i = 0; i <= N; i++) array[i] = -1;
for(int i = 0; i <= M; i++) store[i] = -1;
for( int i = 0; i < N ; i++)
{
cin>>array[i];
for(int j = 0; j< M; j++)
{
if(store[ j ] == array[ i ])
flag = 0;
}
if(flag == 1)
{
store[first] = array[i];
first = (first + 1)%M;
number ++;
}
flag = 1;
}
cout< P1563 玩具谜题


思路:本题考察的是一种方向转换问题。可以使用双链表,数组或者结构体等数据结构。考虑到测试数据的大小和链表操作的繁琐性。本题使用了结构体数组,根据题目操作进行编码。本题关键是仔细画图,确定每次数组下标的加减,把逆时针模拟为反向顺时针,类似补码的思想。
1.定义结构体数组。
2.遍历读入玩具数据,读入操作指令。
3.根据玩具朝向和指令方向通过取模方式模拟玩具圈内的循环过程。
4.指令输入结束,输出结果。
#include
using namespace std;
typedef struct toy{
int a;
char name[11];
}Toy;
int main()
{
Toy toys[100010];
int n, m, derect,number;
cin>>n>>m;
for(int i = 0; i>toys[i].a>>toys[i].name;
int j = 0;
while(m > 0)
{
cin>>derect>>number;
if(derect == 0)
{
if(toys[j].a==1)
j = (j+number)%n;
else
j = (j+n-number)%n;
}
else
{
if(toys[j].a==0)
j = (j+number)%n;
else
j = (j+n-number)%n;
}
m--;
}
cout< P1031均分纸牌
思路:本题考察的是一种算法思路。想明白总体的思想,即可通过。(该思路借鉴了洛谷题解的大佬!)
1.定义变量。
2.计算均值。
3.计算纸牌数值与均值的差值。
4.遍历找到均分不为0移动次数即可加一。input[i+1] += input[i]
#include
#include
using namespace std;
int main ()
{
int number, ave, tot= 0, ans = 0;
int input[102];
cin>>number;
for(int i = 0;i >input[i];
tot += input[i];
}
ave = tot/number;
for(int i = 0; i P1098 字符串的展开
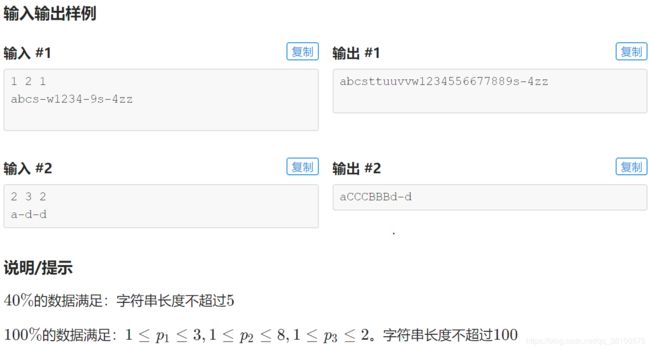
思路:这道题做了很久,后来发现是自己的思考方向不对,做这样的体型应该遵照题意。
1.根据数据规格定义好变量和参数。此处我使用字符串存储,灵活度较低,可以优化。使用字符串要预先计算长度,比如伸展的最大范围:a~z,p2=8的时候就是25* 8* 100 = 20000,即答案的范围。
2.读题,分割条件。同为字母或者数字且分隔符左小于右才会发生字符串的展开。
3.分割小条件控制好输出。
代码:
#include
#include
using namespace std;
char word[102];
char ans[20002];
char change(int p, char x)
{
if(p==1)
{
if('A'<=x&&'Z'>=x)
return x+32;
else
return x;
}
else if(p==2)
{
if('a'<=x&&x<='z')
return x-32;
else
return x;
}
else
return '*';
}
int main()
{
int p1, p2, p3;
cin>>p1>>p2>>p3;
cin>>word;
int i=0,num=0;
char ch;
while(word[i]!='\0')
{
if(i!=0&&word[i]=='-')
{
if(((isdigit(word[i-1])&&isdigit(word[i+1]))||(isalpha(word[i-1])&&isalpha(word[i+1])) )&&(word[i-1]