sEMG信号小波阈值去噪

1.sEMG信号简介

表面肌电信号是从皮肤表面获取的关于肌肉活动的微弱生物电信息，能够为肌肉活动状态分析、神经肌肉功能分析及病理分析等研究提供有效的帮助。由于受到检测仪器、环境和肌肉自身生理特性等多种因素的影响，sEMG信号在采集过程中势必会引入干扰噪声，使得难以直接对其进行分析研究，因而需要对采集到的sEMG信号进行降噪处理，以提高信号质量。

2.小波阈值去噪

2.1小波阈值去噪原理

设$N$点离散含噪信号为
$$f\left(t\right)=s\left(t\right)+n\left(t\right)$$
式中 $s\left(t\right)$ 为原始信号，$n\left(t\right)$ 为服从 $N\left(0,{\sigma }^2\right)$ 的高斯白噪声。
小波阈值法对含噪信号 $f\left(t\right)$ 消噪主要有以下三个步骤：
$\left(1\right)$ 先对含噪信号进行 $j$ 尺度的正交小波变换，得到一组小波系数 ${\omega }_{j,k}$ ；
$\left(2\right)$ 再对 ${\omega }_{j,k}$ 进行阈值处理，确定小波系数的估计值 ${\hat{\omega }}_{j,k}$ ；
$\left(3\right)$ 利用 ${\hat{\omega }}_{j,k}$ 进行小波重构，得到估计信号 $\hat{f}\left(t\right)$ 即为去噪之后的信号。

2.2估计小波系数的方法

$\left(1\right)$ 硬阈值估计法，其定义为
$${\hat{\omega }}_{j,k}=\{\begin{array}{c}{\omega }_{j,k},\left|\begin{array}{c}{\omega }_{j,k}\end{array}\right|⩾\lambda \\ 0,\left|\begin{array}{c}{\omega }_{j,k}\end{array}\right|<\lambda \end{array}$$
$\left(2\right)$ 软阈值估计法，其定义为
$${\hat{\omega }}_{j,k}=\{\begin{array}{c}sgn\left({\omega }_{j,k}\right)\cdot \left(\left|\begin{array}{c}{\omega }_{j,k}\end{array}\right|-\lambda \right),\left|\begin{array}{c}{\omega }_{j,k}\end{array}\right|⩾\lambda \\ 0,\left|\begin{array}{c}{\omega }_{j,k}\end{array}\right|<\lambda \end{array}$$

2.3小波阈值选取

$\left(1\right)$ 全局阈值
$$\lambda =\sigma \sqrt{2lnN}$$
$\left(2\right)$ SUREShrink阈值
使用斯坦因的无偏风险估计(SURE)原理进行自适应阈值选择
$\left(3\right)$ Minimax阈值​​

3小波基函数和分解层数选择

3.1小波基函数选择

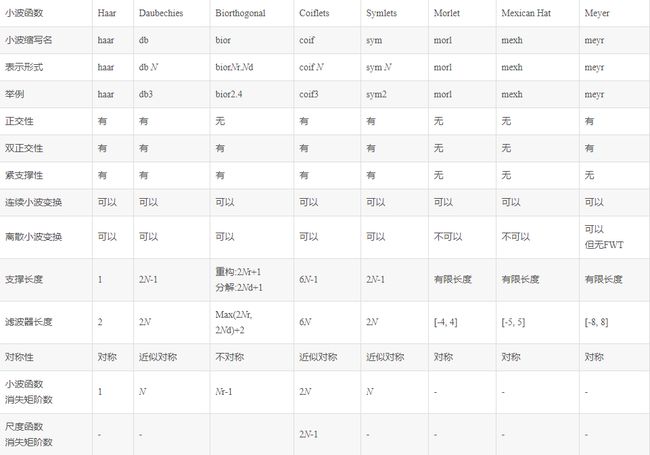
对含噪的sEMG信号进行小波分解，更具Mallat最优小波基的选择准则，综合考虑小波基的对称性、正交性、消失矩及紧支性等数学特征最终选择Sym8小波基，因为它的尺度函数波形与sEMG信号波形近似，小波函数的对称性较好。下图为常见小波的数学特征：

3.2分解层数选择

分解层数对于消噪效果的影响很大，分解层数过多信号失真也会越大，还会导致运算量增大，处理变慢。分解层数过少则消噪效果不理想。
实验所使用的sEMG信号的采样频率为1000Hz,，根据奈奎斯特采样定理可知，信号的最高频率可为500Hz。如果进行4层小波分解，对应的每层频带范围如下图所示，其中$a_i$表示近似系数，$d_i$表示细节系数。
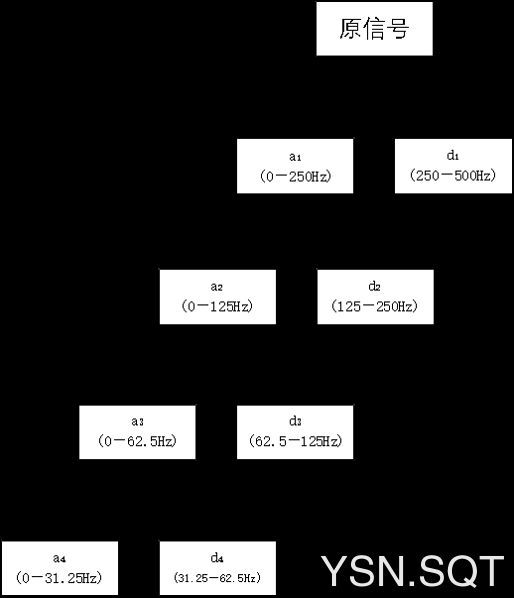观察表面肌电信号的频域情况，发现能量在300Hz以下的部分占全部能量的80%，主要集中在50至220Hz之间。由此可得，分解次数选择4层。

4小波阈值去噪matlab实现

4.1wavelet signal denoiser

wavelet signal denoiser是matlab用于可视化去噪一维信号并比较去噪效果的交互式工具，可以轻松调整默认参数并应用不同的降噪技术。
打开方式：
$\cdot$ Toolstrip：在工具栏中，选择应用程序，找到信号处理和通信下的wavelet signal denoiser，单击选择打开。
$\cdot$ 命令提示符：在命令窗口，输入 waveletSignalDenoiser，并运行。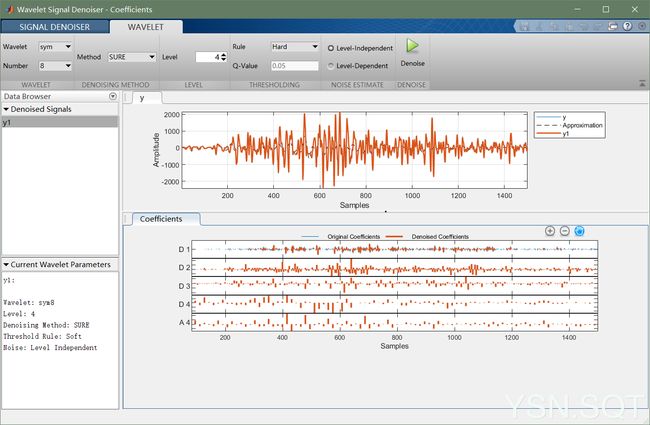

4.2matlab批处理文件

实验所采集的数据很多，通常都是同类型的数据，处理方式等大都相同，采用文件批处理可以大大减少操作步骤，提高效率。
matlab代码：

list=dir('E:\sEMG_data\*.mat');
k=length(list);
for i=1:k
    load(list(i).name)
    for j=1:4
        Y=data{:,j};
        Y = wdenoise(Y,4, ...
            'Wavelet', 'sym8', ...
            'DenoisingMethod', 'SURE', ...
            'ThresholdRule', 'Hard', ...
            'NoiseEstimate', 'LevelIndependent');
    end
end

MATLAB中小波去噪: https://www.mathworks.com/help/wavelet/ref/wdenoise.html.
wavelet signal denoiser: https://www.mathworks.com/help/wavelet/ref/waveletsignaldenoiser-app.html.
参考文献: http://www.cnki.com.cn/Article/CJFDTotal-XXYK201102003.htm.