软件工程项目 数独
软件工程项目 数独
项目的Github地址
PSP表格
| PSP2.1 | Personal Software Process Stages | 预计耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| ·Estimate | 估计这个任务需要多少时间 | 20 | 40 |
| Development | 开发 | ||
| ·Analysis | 需求分析(包括学习新技术) | 480 | 600 |
| ·Design Spec | 生成设计文档 | 120 | |
| ·Design Review | 设计复审(和通识审核设计文档) | —— | —— |
| ·Codeing Standard | 代码规范(为目前的开发设定合适的规范) | 30 | 30 |
| ·Design | 具体设计 | 120 | 200 |
| ·Coding | 具体编码 | 300 | 500 |
| ·CodeReview | 代码复审 | ||
| ·Test | 测试(自我测试,修改代码,提交修改) | 120 | 600 |
| Reporting | 报告 | ||
| ·Test Report | 测试报告 | 120 | 150 |
| ·Size Measurement | 计算工作量 | 30 | 20 |
| ·Postmortem & Process Improvement Plan | 事后总结,提出过程的改进计划 | 60 | |
| 合计 | 1460 | 2200 |
解题思路
这次的软件工程项目与之前所接触的代码作业都不太相同,写代码只占了其中的一小部分。有很多的要求都需要做新的学习,比如git的使用,文档的编写,代码的分析等。
对此次作业的任务进行分解:
- 数独生成与解决的算法
- 对于代码的完善和各种测试
- 文档和博客的编写,项目的管理
之中有很多没有使用和了解过的东西,估计学习过程够呛。
工欲善其事必先利其器,首先是各种前置技能的学习。大致的了解过后,对于项目需不断在GitHub上更新进展,所以本地不断更改一气呵成再完成其它工作的方式是不行的了。
教程和相关知识的搜寻就通过搜索引擎搜索就好。
先对github的操作进行学习,这里引用一个教程
https://blog.csdn.net/qq_35246620/article/details/66973794
对基础工具了解之后,开始学习数独的生成于求解。
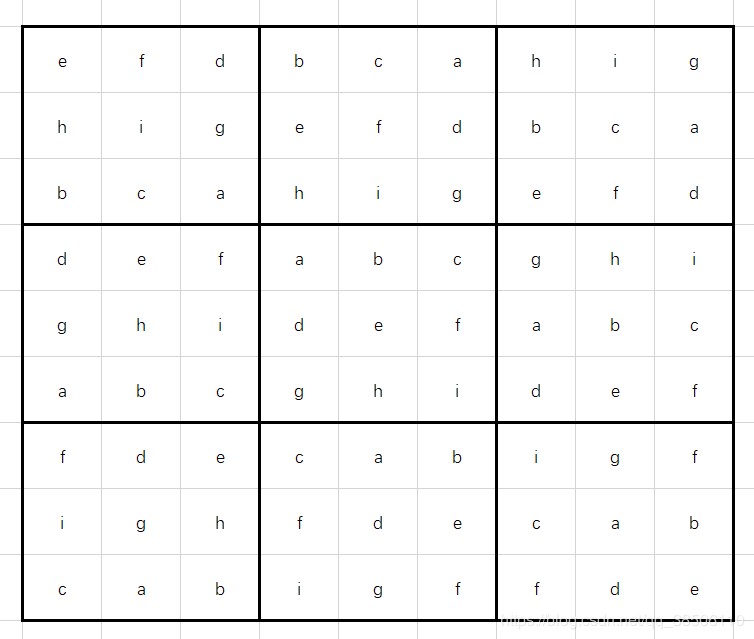
生成看似是个简单的回溯问题,但直接暴力求解肯定是无法满足性能上的要求的,参考网上一个思路,将数独的第五宫作为种子,就能生存其余八个宫。
由一个宫生成其余八个宫,自己写了写就发现其中规律如此明显。对一个块进行行列的平移就完全能实现了。
种子有 8 ! 8! 8! 种情况,每个种子经过平移生成的数独棋局又有 2 ! ∗ 3 ! ∗ 3 ! ∗ 2 ! ∗ 3 ! ∗ 3 ! 2!* 3!*3!*2!*3!*3! 2!∗3!∗3!∗2!∗3!∗3! 种变换。其总和超过了任务所需的1000000个,此方案可行。
对于各种全排列,打算采用递归的方式实现,在最后生成终局的时候采取一些映射的小技巧来减少时间。
仔细想了想上述的全排列,发现很明显其中有重复的结果。行列变换后的结果会与全排列产生的序列重合。根据我的构建方法,只要第一宫产生了相同的状况那就一定会出现重复的情况。想明白错误产生原因之后就很好处理了。对行列变换时不对第一宫进行变换,能够产生的结果数为 8 ! ∗ 3 ! ∗ 3 ! ∗ 3 ! ∗ 3 ! = 52 , 254 , 720 8!*3!*3!*3!*3!=52,254,720 8!∗3!∗3!∗3!∗3!=52,254,720,总数依然超过题目要求的一百万。
数独的求解,参考dancinglinks 算法进行高效的求解,最开始因考虑到整个全覆盖可能是稀疏矩阵于是直接采用链表的方式来实现。但是考虑到若是大量的数独求解每次新数独的初始构造和结束后的释放会占用大量的时间。所以更换利用数组实现。
设计实现过程
类的实现
设计时将整个程序分为三个类。由main函数来分别调用这三个类。三个类之间不存在相互的依赖关系。
Check 类用来实现对于命令行参数的检查,包括参数的个数,参数是否正确,如果不正确则返回错误信息。 在参数正确的情况下,为main函数提供反馈信息,告知其是求解还是生成。main函数根据结果调用相应的类进行处理。
SolveSudoku类用来对数独进行求解。为了实现其功能独立,设立一个public的方法startSolve后所有的求解与输出过程均在类的内部进行。
在解决数独问题的过程中,因为需要进行回溯的操作,需要将回溯单独写在一个函数中。
CreateSudoku类用来生成数独的终局,也是一个public方法调用后其余部分均在内部完成。
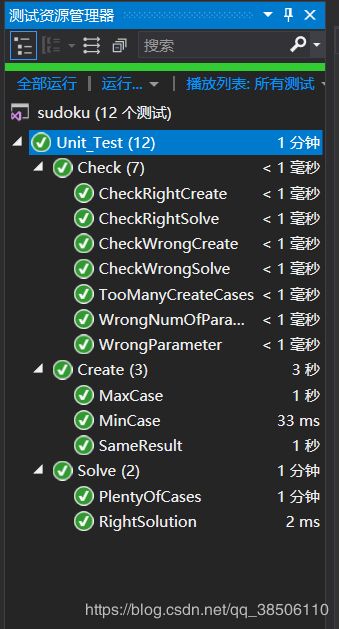
单元测试
c++以类为对象进行单元测试。
Check类设计了单元测试来测试不同的命令行参数的结果
CreateSudoku对于生成的数独进行了重复性检测,生成1000000数独对其进行重复性检查。因为电脑性能的问题,检测前100000个便花费了两小时后终止了测试,但其中没有发生重复。之后测试考虑可行性的问题对其10000以内进行测试。
同时也对1个数独的生成,1000000的生成进行了检查。
SolveSudoku对求解的所有的结果都进行了合法性检查,分别为高难度的数组和大量(1000000)的普通数独求解后分别计算了其解是否合法。
性能分析
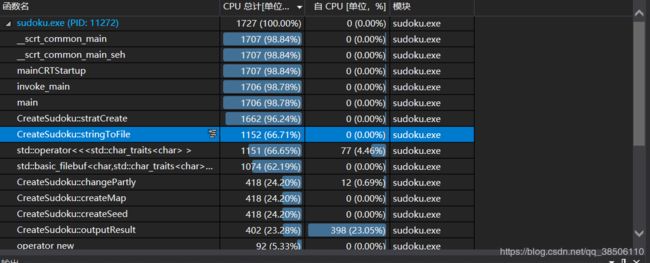
首先针对数独终局的生成进行性能测试。生成了1000000个数独,耗时2秒以内,还算较为理想的结果。
针对20个难解数独进行运行分析性能。
首先是利用链表来实现dancinglink,但是在实现过程中发现new与delete会占据大量的时间,所以利用数组来实现dancinglink的算法。
第一次性能分析结果如下
花费了大量的时间在回溯上,采取解决的措施。每次选择可能性最小的位置进行填写。
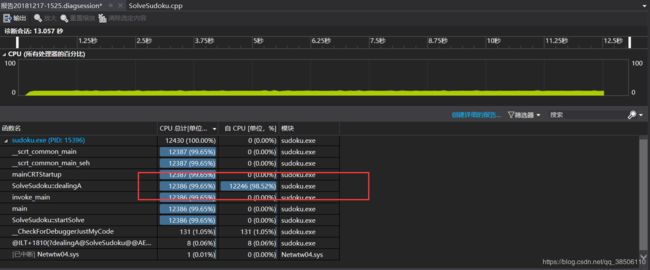
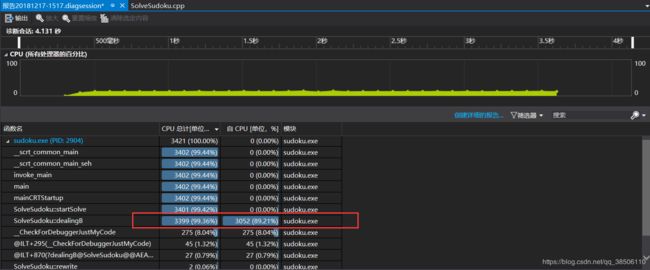
更改之后的性能分析,时间大部分花费在了链表的移除和恢复上。
在之后,为了确认dancinglink的速度和传统数独解法之间的差异,又再次实现了传统的数独解法。
两个解法相比较耗时的部分各有差异。dancinglink有大部分的耗时是在链表的移除和恢复操作中。而传统的回溯解法反而是浪费了大量的时间在回溯上。但性能还是优于dancinglink。
代码说明
对于生成数独的部分,为了节约内存和减少各种赋值的时间,没有直接对数独进行行列变换。而是直接对其坐标进行了全排列。相当于引入了一个映射。
bool CreateSudoku::createMap() //利用3*3的第一宫平移获得整个数独
{
int i, j, k, l, m;
for (i = 0, k = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
sudoku[i][j] = seed[k++];
for (l = 0; l < 3; l++) {
for (m = 0; m < 3; m++) {
sudoku[(i + m) % 3 + 3 * l][(j + l) % 3 + m * 3] = sudoku[i][j];
}
}
}
}
changeMap();
return true;
}
void CreateSudoku::changePartly(int * a, int start, int end) //将坐标映射进入一维数组分段进行全排列
{
int i;
if (start == end) { //分段进行全排列,完成后直接获取结果
if (end == 5) {
changePartly(a, 6, 8);
}
else if (end == 8) {
changePartly(a, 12, 14);
}
else if (end == 14) {
changePartly(a, 15, 17);
}
else {
getResult();
}
}
else {
for (i = start; i <= end; i++) {
swap(a, start, i);
changePartly(a, start + 1, end);
if (nowNumber == goalNumber) break; //满足需要的数独个数后立即终止全排列
swap(a, start, i);
}
}
return;
}
求解的时候设置了判断变量,分别分析行、列、宫填入一个数字是否满足,为了提高速度运用了bitmap的方法采取了int型利用位运算来快速判断。
求解部分花费时间最长的代码如下:
bool SolveSudoku::dealingB(int* criterion, int i, int j)
{
int k;
bool state = false;
for (; i < 9; i++) {
for (; j < 9; j++) {
if (map[i][j] == 0) {
state = true;
break;
}
}
if (state) {
break;
}
j = 0;
}
if (!state) {
return true;
}
int value;
state = false;
for (k = 0; k < 9; k++) {
value = k + 1;
if (!fill(i + 1, j + 1, value, criterion)) {
continue;
}
map[i][j] = value;
removeA(criterion, i + 1, j + 1, value);
state = dealingB(criterion, i, j);
if (state) {
break;
}
recoverA(criterion, i + 1, j + 1, value);
map[i][j] = 0;
}
return state;
}
收获
之前也做过许多的项目,但是大部分也是只要最后上传到网教结果成功了即可,并没有做太多的性能上的要求。
本次项目,不仅要求代码的成功运行,还有许多额外需要完成的东西。
github也是一个自己一直想尝试但总因为各种各样的理由推脱没有落实的。这次算是完成了一个学习目标。
除此之外,还接触了单元测试,代码覆盖率等之前没有了解到的知识点。
最后是网上资料的查询,对于所有的资料,可能会包含一些错误,在自己落实的过程中又需要有自己的思考来完成错误的修正。当自己实践之后才知道理论的对错。