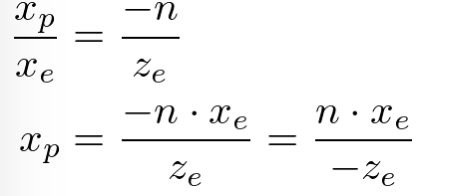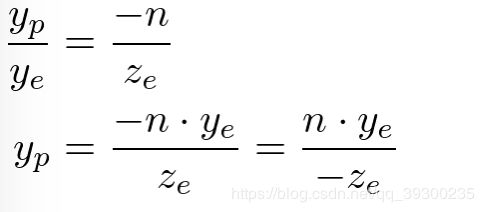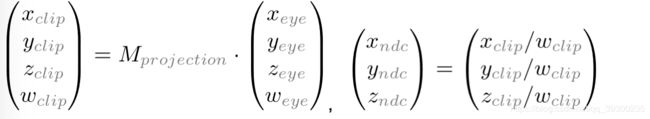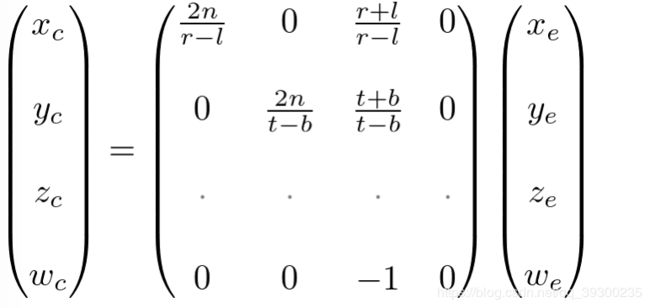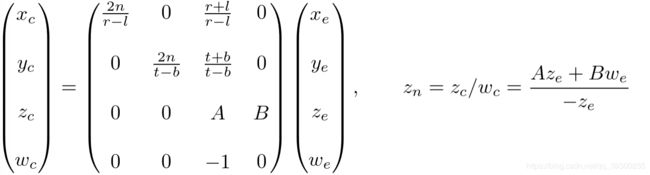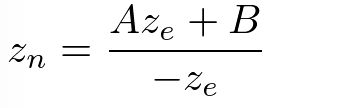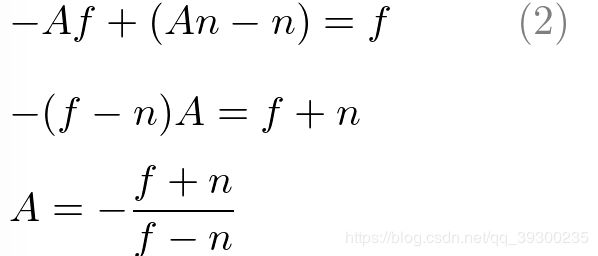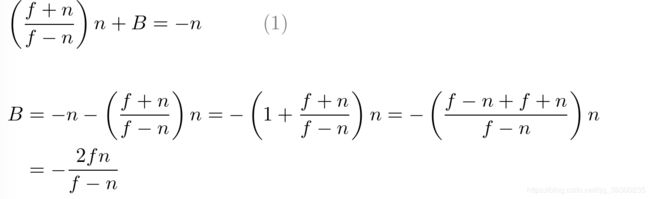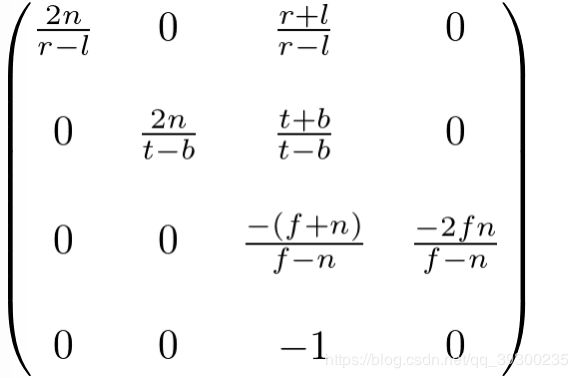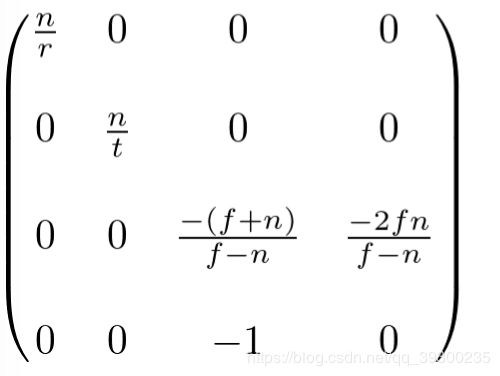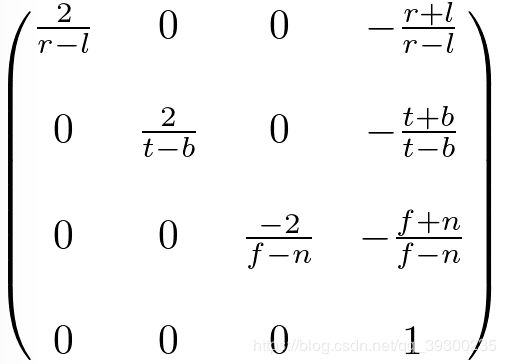OpenGL中投影矩阵(Projection Matrix)详解

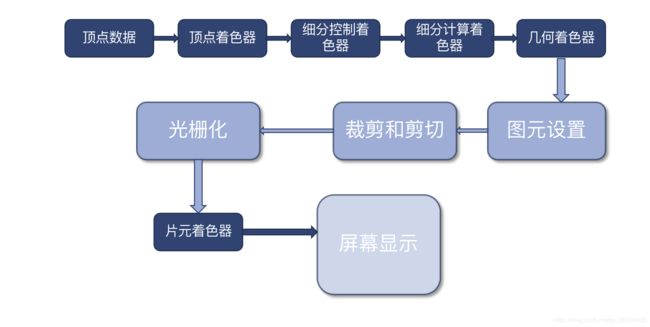
在游戏开发中，一个物体模型从它自身的坐标系转换至我们在屏幕上所见的样子，需要进行一系列的坐标变换以及其他的操作。该过程称为渲染管线。以OpenGL为例：

该过程在以前是被封装的，不能访问。但是现在我们可以对该过程进行更改，所以该过程现在也称为OpenGL的可编程渲染管线。

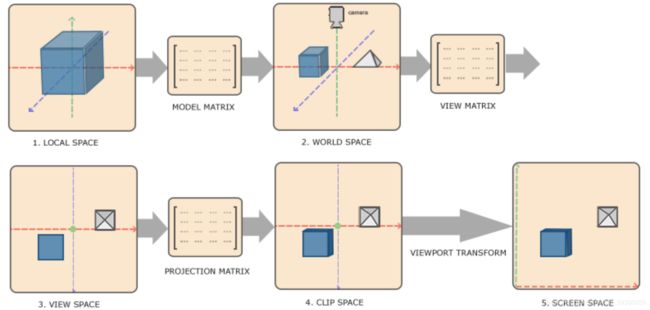
而我们把顶点数据发送给我们的顶点缓冲后，在顶点着色器中，我们需要完成一个从模型本地坐标变换到投影坐标到变换。

如图所示，我们首先需要将本地空间，通过使用模型矩阵将其转换至世界空间。再通过视口矩阵，将其转换为视口空间。之后再乘上投影矩阵，就将视口空间转换为裁剪空间。最后进行裁剪等操作使裁剪空间转换为屏幕空间。

 

投影矩阵

改文章重点讲解使用投影矩阵的原因，以及投影矩阵的数学原理。计算机的显示屏是一个2D平面。一个3D的场景需要通过投影矩阵渲染在2D图像中。投影矩阵使用了投影变换。首先，它将所有的视口坐标转换至剪切坐标。然后这些裁剪坐标还会通过除以裁剪坐标的w分量来转换成标准设备坐标(NDC). 投影矩阵分为透视(Perspective)投影和正交(Orthographic)投影。

        

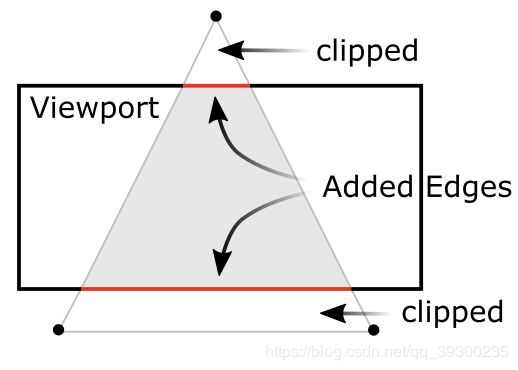
接下来将会阐述如何通过6个约束参数：left, right, bottom, top, near and far 来建立投影矩阵。我们要先注意平截头体的裁剪是在裁剪空间进行的，仅仅在除以Wc之前。在裁剪坐标中，Xc，Yc，Zc都要和Wc进行对比，若裁剪坐标小于-Wc或者大于Wc，则被裁减。保留：。当被裁减过后，OpenGL会自动生成被裁减的边缘。

透视投影

 

 

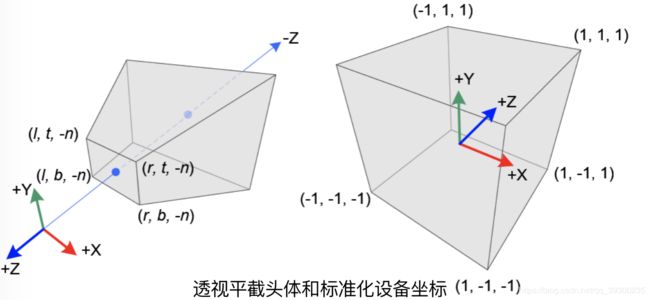
在透视投影中，截断的锥体平截头体（视口坐标）中的3D点被映射到立方体（NDC）; 从[l，r]到[-1,1]的x坐标范围，从[b，t]到[-1,1]的y坐标和来自[-n，-f]的z坐标 到[-1,1]。

请注意，视口坐标是在右手坐标系中定义的，但NDC使用左手坐标系。 也就是说，原点处的相机沿着视口空间中的-Z轴看，但它在NDC中沿着+ Z轴看。                   

在OpenGL中，视口空间中的3D点被投影到近平面（投影平面）上。 下图显示了视口空间中的点（Xe，Ye，Ze）如何投射到近平面上的（Xp，Yp，Zp）。

从平截头体的顶视图，视口空间的X坐标，Xe被映射到Xp，其通过使用相似三角形的比率来计算;

然后通过相似的方法计算平截头体的左视图中的Yp；

注意Xp和Yp都取决于Ze; 它们与-Ze相反。 换句话说，它们都被-Ze除。 这是构建投影矩阵的第一个线索。 在通过乘以投影矩阵变换适口坐标空间（view space）之后，裁减坐标仍然是齐次坐标。 它最终通过除以剪辑坐标的W分量变为标准设备坐标（NDC）。 

因此，我们可以将裁减坐标的w分量设置为-Ze。 并且，投影矩阵的第4行变为（0, 0,-1, 0）。

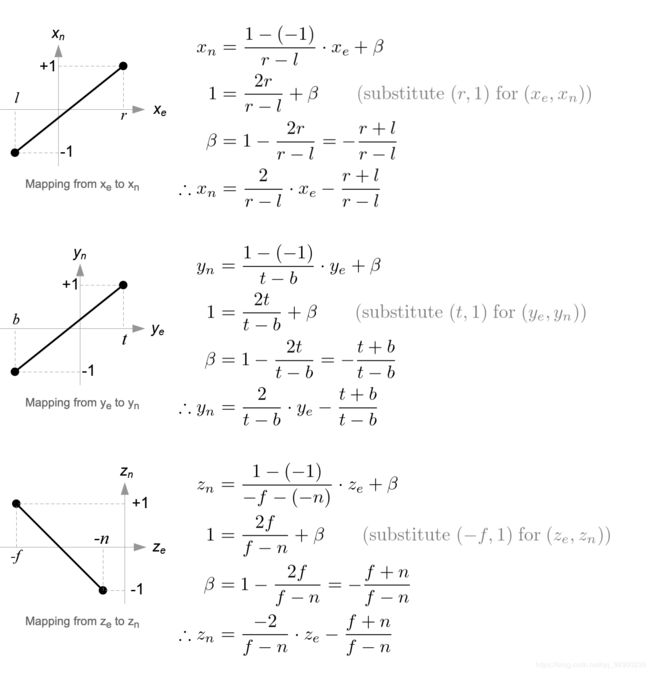
接下来，我们将Xp和Yp映射到具有线性关系的NDC的Xn和Yn; [l，r]⇒[-1,1]和[b，t]⇒[-1,1]。

然后，我们将Xp和Yp替换为上述等式。

请注意，我们使每个方程的两个项都被-Ze整除为透视除法（Xc / Wc，Yc / Wc）。 我们将Wc设置为-Ze，括号内的术语变为剪辑坐标的Xc和Yc。

从这些方程式中，我们可以找到投影矩阵的第1行和第2行。

现在，我们只有第3行的投影矩阵需要解决。 寻找Zn与其他的略有不同，因为视口空间中的Ze总是被投射到近平面上的-n。 但是我们需要用于裁减和深度测试的唯一Z值。 另外，我们应该能够取消投影（即逆变换）它。 因为我们知道Z不依赖于X或Y值，所以我们借用W分量来找到Zn和Ze之间的关系。 因此，我们可以像这样指定投影矩阵的第3行。

在视口空间中，We等于1。因此，等式变为:

为了找到系数A和B，我们使用（Ze，Zn）关系; 如（-n，-1）和（-f，1），并将它们放入上面的等式中。

为了求解A和B的等式，重写B的等式（1）;

将方程（1'）代入方程（2）中的B，然后求解A;

将A代入方程（1）中以算出B;

我们得到了A和B。因此Ze和Zn之间的关系变成了:

最后，我们找到了投影矩阵的所有信息。 完整的投影矩阵是:

该投影矩阵用于一般的截头体。 如果观察体积是对称的，那么它就是,，并且可以简化为:

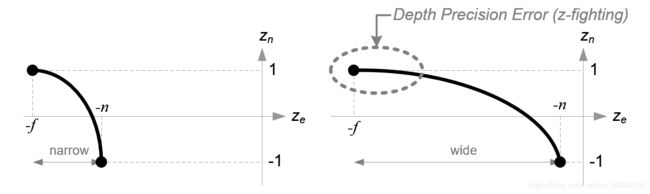
在我们继续之前，请再次看一下Ze和Zn，eq.(3）之间的关系。 您注意到它是一个有理函数，并且是Ze和Zn之间的非线性关系。 这意味着近平面的精度非常高，但远平面的精度非常低。 如果范围[-n，-f]越来越大，则会导致深度精度问题（z-fighting）; 远处平面周围的小的Ze变化不会影响Zn值。可以使 n和f之间的距离应尽可能短，以最小化深度缓冲精度问题。

这个非线性的特点在游戏中会有非常大的优点，因为我们在进行深度测试的时候，距离摄像机近的点在深度测试具有非常高的精度，而远处的点在深度测试的时候会有较低的精度。而这正是我们需要的。

 

正交投影

构造用于正投影的投影矩阵比透视模式简单得多。                                                                                                          

视口空间中的所有Xe，Ye和Ze分量线性映射到NDC。 我们只需要将矩形体积缩放到立方体，然后将其移动到原点。 让我们使用线性关系找出投影矩阵的元素。

由于正交投影不需要W分量，因此投影矩阵的第4行保持为（0,0,0,1）。 因此，正交投影的完整投影矩阵是：

如果观察体积是对称的，，，则可以进一步简化。