Graph Convolutional Network (图卷积GCN)
直觉上想要找到构图结点的特征,一定是与其相关的结点、连接的边有关。那么就直接把每个顶点比如1号结点相邻的结点找出来,虽然相邻的个数可能不一样,设个最大值,不够的就补0,然后类似onehot一下,变成统一维度来做不就ok了?但是这样做的缺点在于,必须每个顶点都处理,而且而且而且效果一般。
但是我们有图论,甚至还有拓扑学!
卷积与图卷积
既然思路是从某点与其点的周围,这属于局部信息。而对每个点进行操作,每个点的周围会有重复,叠加。这不就是卷积?(某一个东西和另一个东西在某种度上如时间或空间的“叠加”作用,实现局部加权平均,以信号增强),可是CNN是图像,是结构化的数据,和非结构的图有共通点吗?
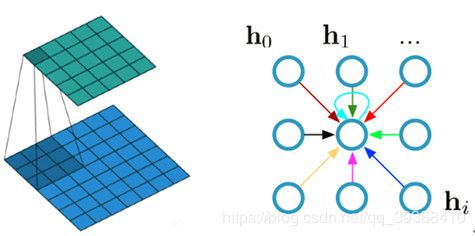
实际上CNN可以看成是GCN的某特殊形式。那么按照CNN的思路,首先构造一个规整的结构化矩阵。但是由于图的顶点数,度数会不一样,所以产生了频域方法,它的本质动机就是把顶点域的卷积转化为频域里的乘积再求逆傅里叶变换。在频域中,非euclidean的事物就变得euclidean了。
首先对于图,自然使用邻接矩阵:

对于一个图G=(V,E),上面三个的三个矩阵分别是度矩阵D,邻接矩阵A和拉普拉斯(Laplacian)矩阵,其中拉普拉斯矩阵的定义是L=D-A。
对照CNN是局部局域和卷积核进行乘积,GCN也就能直接得到一个节点的原始特征X与邻接矩阵A相乘后,再有个权重W进行调整滤波,最后再激活函数:
f ( X , A ) = σ ( A X W ) f(X,A) =\sigma(AXW) f(X,A)=σ(AXW)
这样就可以理解为对每个节点整合了邻居节点的特征向量,同时考虑到CNN中是的那个中心点是有自环的(如上上图),即有自己的信息,那么对于邻接矩阵需要加上一个一个单位矩阵I,同时对这个式子归一化防止数值不稳定和梯度爆炸(因为A并不是归一化的,形态会类是椭圆)就得到了一个简单却有效的式子:
f ( X , A ) = σ ( I + D − 1 / 2 A D − 1 / 2 X W ) = σ ( D ‾ − 1 / 2 ( A + I ) D ‾ − 1 / 2 X W ) f(X,A) =\sigma(I+D^{-1/2}AD^{-1/2}XW)=\sigma(\overline{D}^{-1/2}(A+I)\overline{D}^{-1/2}XW) f(X,A)=σ(I+D−1/2AD−1/2XW)=σ(D−1/2(A+I)D−1/2XW)
D ‾ − 1 / 2 \overline{D}^{-1/2} D−1/2的原因是在矩阵中,左乘和右乘是不一样的,需要归一得矩阵需要两边各自1/2。
编码直接利用这个式子就可以了,其中 X ∈ R N × C 和 A ∈ R N × N 和 D ∈ R N × C X \in R^{N \times C} 和 A \in R^{N \times N} 和 D \in R^{N \times C} X∈RN×C和A∈RN×N和D∈RN×C
class GraphConvolution(nn.Module):
def __init__(self, in_features, out_features, bias=False):
super(GraphConvolution, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.Tensor(in_features, out_features))
if bias:
self.bias = Parameter(torch.Tensor(1, 1, out_features))
else:
self.register_parameter('bias', None)
def forward(self, input, adj):
support = torch.matmul(input, self.weight)
output = torch.matmul(adj, support) #adj矩阵会提前计算
if self.bias is not None:
return output + self.bias
else:
return output
完整的细节源代码逐行中文注释:https://github.com/nakaizura/Source-Code-Notebook/tree/master/GCN
其实上面的式子只是一个直观的猜想,即图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。还需要有图论背后的支持:GCN的paper:https://arxiv.org/abs/1609.02907. 网络上的各自解析很复杂但也很必要,比如知乎高赞回答https://www.zhihu.com/question/54504471/answer/153095639 。
下面是博主自己理解的思路。
节点归一化
单个节点运算来说,做归一化就是除以它节点的度,这样每一条邻接边信息传递的值就被规范化了!所以使GCN能够直接处理一个矩阵,不用关心每个节点的邻居数都是不一样而权重数目就不一样。这也是为什么非要搬出拉普拉斯,傅里叶,切比雪夫三座大山的核心,我们需要聚合。
滤波器应该滤什么?
如果要开始卷积的话,应该是对信号X做卷积核或者也称滤波器 g θ = d i a g ( θ ) g_\theta=diag(\theta) gθ=diag(θ)的处理,那么对于“滤波”到底需要滤出什么?对于每个图结点,相乘的矩阵应该是最能代表这个结点周边关系的局部特征,但是我们只有邻接矩阵。
不过对于N个结点的图来说,邻接矩阵也会是N维的,会有N个特征值,特征值代表了该特征在空间内的放缩程度,而特征向量是它的指向。那么如果能对矩阵进行分解,得到能够代表局部特征的矩阵就太好了。(按照频率的观点:即会有n个频率,那么按照频率分解,得到的就是每个节点的特征表达了,这里实际上就将图这种非欧结构通过傅里叶转换成了欧式空间)
为了方便分解,不直接使用邻接矩阵而是利用拉普拉斯矩阵。
为什么拉普拉斯
对矩阵的特征分解,绕不开的就是谱分解,其实谱分解的“谱”,就是矩阵的相异特征值,即按照特征值进行分解。
话不多说,先做一题线代。
问:求矩阵A=[[1 2 2],[2 1 2],[2 2 1]]的谱分解。
- 先得到特征多项式 ∣ λ E − A ∣ = ( λ − 1 ) 2 ( λ − 5 ) |\lambda E-A|=(\lambda-1)^2(\lambda-5) ∣λE−A∣=(λ−1)2(λ−5),可得特征值为-1和5,特征向量为 x 1 x_1 x1=[1 -1 0]^T , x 2 x_2 x2=[1 0 -1]^T, x 3 x_3 x3=[1 1 1]^T.
- 再设 λ \lambda λ对应的左特征向量为 y 1 T , y 2 T , y 3 T y_1^T,y_2^T,y_3^T y1T,y2T,y3T,由特征分解定理,如果X是线性无关右向量,Y是线性无关左向量有, X Y T = E XY^T=E XYT=E(因为对角化 A = P Λ P − 1 = Λ X Y T = Λ E ) A=P\Lambda P^{-1}=\Lambda XY^T=\Lambda E) A=PΛP−1=ΛXYT=ΛE)。
- 那么求出 P − 1 = [ 1 / 3 − 2 / 3 1 / 3 1 / 3 1 / 3 − 2 / 3 1 / 3 1 / 3 1 / 3 ] P^{-1}=\left[ \begin{matrix} 1/3 & -2/3 & 1/3 \\ 1/3 & 1/3 & -2/3\\ 1/3 & 1/3 & 1/3 \end{matrix} \right] P−1=⎣⎡1/31/31/3−2/31/31/31/3−2/31/3⎦⎤
- 那么就得到了线性无关左向量Y, y 1 T y_1^T y1T=[1/3 -2/3 1/3], y 2 T y_2^T y2T=[1/3 1/3 -2/3], y 3 T y_3^T y3T=[1/3 1/3 1/3]。
- 则 E 1 = [ x 1 x 2 ] [ y 1 y 2 ] T = [ 1 1 − 1 0 0 − 1 ] ∗ [ 1 / 3 − 2 / 3 1 / 3 1 / 3 1 / 3 − 2 / 3 ] E_1=[x_1 x_2][y_1 y_2]^T=\left[ \begin{matrix} 1 & 1 \\ -1 & 0 \\ 0 & -1 \end{matrix} \right]*\left[ \begin{matrix} 1/3 & -2/3 & 1/3 \\ 1/3 & 1/3 & -2/3 \end{matrix} \right] E1=[x1x2][y1y2]T=⎣⎡1−1010−1⎦⎤∗[1/31/3−2/31/31/3−2/3]
- E 2 = x 3 y 3 T E_2=x_3y_3^T E2=x3y3T=…
- 从而 A = − E 1 + 5 E 2 A=-E_1+5E_2 A=−E1+5E2
就是可以根据特征向量,找出两个矩阵来表示原矩阵。所以不仅能分解,分解之后的矩阵还有各种性质,十分方便。但是只有对角化矩阵才能够谱分解(即需要A有n个线性无关的特征向量)。所以拉普拉斯矩阵多厉害:
- n个线性无关的特征向量
- 半正定
- 对称矩阵特征向量正交
一定可以谱分解不说,因为特征向量正交,分解后比上面的题目结果还漂亮, L = U λ U − 1 = U λ U T L=U\lambda U^{-1}=U\lambda U^T L=UλU−1=UλUT,因为正交,连矩阵逆都不用求,知道特征值与特征向量就完成了。
为什么傅里叶?
因为用傅里叶变化做基,特征值都不用算。
任何可积的函数都可以用傅里叶来做逼近,而特征值本身也代表着这种不变的频率,所以做傅里叶变换相当于对特征积分
f ′ ( i ) = ∑ i N f ( i ) u i ∗ ( i ) f'(i)=\sum_i^N f(i)u_i^*(i) f′(i)=i∑Nf(i)ui∗(i)即和 u i ∗ ( i ) u_i^*(i) ui∗(i)特征向量的第i个分量,做内积。所以如果对卷积做傅里叶变换,卷积可以表示成:
g θ ∗ X = U g θ U T X g_{\theta}*X=Ug_{\theta}U^TX gθ∗X=UgθUTX对比 L = U λ U − 1 = U λ U T L=U\lambda U^{-1}=U\lambda U^T L=UλU−1=UλUT,滤波操作 g θ g_{\theta} gθ其实就可以理解成是L的特征值函数,就完成了我们想要把对应特征分解的初衷,且不需要特意计算特征值,有滤波器就好。
为什么切比雪夫
然而矩阵相乘的非常昂贵( O ( N 2 ) O(N^2) O(N2)),切比雪夫逼近 之后,矩阵将不需要再分解,而且可以得到任意阶的展开。
g θ ′ ≈ ∑ k = 0 k θ k ′ T k g_{\theta'} \approx \sum_{k=0}^k \theta_k' T_k gθ′≈k=0∑kθk′Tk即用切比雪夫多项式来近似 g θ g_{\theta} gθ, T k = 2 X T k − 1 − T k − 2 , T 0 = 1 , T 1 = X T_k=2XT_{k-1}-T_{k-2},T_0=1,T_1=X Tk=2XTk−1−Tk−2,T0=1,T1=X,相当于选用一个好的卷积核后,可以抵消掉计算U,也就不需要分解了,直接拿拉普拉斯矩阵算切比雪夫k阶(相邻到k个邻居)近似就ok,也就是那个直观的式子:
f ( X , A ) = σ ( I + D − 1 / 2 A D − 1 / 2 X W ) = σ ( D ‾ − 1 / 2 ( A + I ) D ‾ − 1 / 2 X W ) f(X,A) =\sigma(I+D^{-1/2}AD^{-1/2}XW)=\sigma(\overline{D}^{-1/2}(A+I)\overline{D}^{-1/2}XW) f(X,A)=σ(I+D−1/2AD−1/2XW)=σ(D−1/2(A+I)D−1/2XW)
拉普拉斯的意义?
拉普拉斯来源于拉普拉斯算子,它是n维欧式空间的二阶微分算子,当它退化到离散的二维图像空间,可以变成边缘检测算子[[0 1 0][1 -4 1][0 1 0]],即它描述了中心像素与局部上下左右邻居的像素差异。
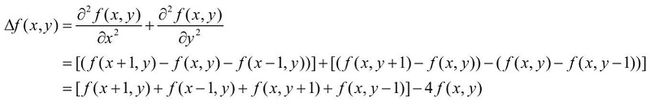
所以,拉普拉斯矩阵可以看成是一个反映图信号局部平滑度的算子,进一步它可以定义一个很重要的二次型: x T L x = ∑ v i ∑ N ( v i ) x i ( x i − x j ) = ∑ e i j ∈ E ( x i − x j ) 2 x^TLx=\sum_{v_{i}}\sum_{N(v_i)}x_i(x_i-x_j)=\sum_{e_{ij} \in E}(x_i-x_j)^2 xTLx=vi∑N(vi)∑xi(xi−xj)=eij∈E∑(xi−xj)2简直不要太酷了,可以理解为边信号的差值加和,刻画整体信号的平滑度。
multi-layer
所以本质上对比普通的NN,GCN只是在特征上做了一个变换,而这个变换的实质就是特征通过拓扑结构进行了传播,是自身和其邻居节点的特征加权求和。所以当GCN也按照NN的思路进行多层抽象的时候,由于后面层中的每个节点是更新过的节点,即变化后的特征,可以理解为每个节点接收到了2-hop的信息,感受域进一步增加。
semi-GCN
GCN的提出是为了做这种半监督的分类任务。传统方法是假设“相连节点应该相似,具有相同标签”,但很明显节点之间应该既有共性也有个性,这个假设太严格了,极大限制模型能力。但是图结构反映了节点之间的相似性或者存在关系这一点没有异议,那么利用部分有标签的数据做监督,或者说是加入很多未标记的样本,反而是能够提升“泛化”,提升模型效果的。
GCN的缺点
- over-fitting。如果数据量很少的情况下容易发生。
- vanishing gradient。这也是NN的老问题梯度消失。
- over-Smoothing。由于堆叠多层GCN ,节点考虑的邻居阶数也会越多,本身它就是个普通的拉普拉斯平滑,会慢慢导致最终所有节点的表示会趋向于一致,同质化。【一旦层数加起来,GCN的衰退真是超级明显,所以一般不做其他处理,最多搭到三层的浅层模型】
GCN的局限性
- 无法inductive(处理动态图)。inductive任务是指:训练阶段与测试阶段需要处理的graph不同。通常是训练阶段只是在子图上进行,测试阶段需要处理未知的顶点。
- 无法处理有向图,不容易实现分配不同的学习权重给不同的neighbor。
- 如何在大图上也做有效的训练。
于是就有了GraphSAGE,GAT等解决方案。