纹理特征一:GLCM---灰度共生矩阵
纹理特征一:GLCM 灰度共生矩阵
1. GLCM 的解释与计算
假设: GLCM(Gray-level co-occurence matrix,灰度共生矩阵)是20世纪70年代初由R.Haralick等人提出的。该方法基于的假设是:图像纹理的变化和色素的空间分布有关。
计算: 设图上一点 ( x , y ) (x,y) (x,y)与一个距离固定的点 ( x + d , y + l ) (x+d,y+l) (x+d,y+l),两点的灰度值分别(g1, g2),之后移动 ( x , y ) (x,y) (x,y),将得到不同的(g1, g2)。如果该图的灰度等级为k,则不同的(g1, g2)的值种类最多为 k 2 k^2 k2个。灰度共生矩阵就是对这些不同的(g1, g2) 值的个数统计。
这里的d和l可以取不同的值。
- d = 1,l = 0:水平方向的GLCM;
- d = 0,l = 1:垂直方向上的GLCM;
- d = 1,l = 1: 4 5 。 45^。 45。上的GLCM;
- d = -1,l = 1: 13 5 。 135^。 135。上的GLCM。
举例解释: 如下图,图(a) 是一个图像的像素值,图(b)是GLCM中各元素对应的(g1,g2)。图©、图(d)、图(e)、图(f)分别是沿水平方向、垂直方向、 13 5 。 135^。 135。、 4 5 。 45^。 45。方向上计算的GLCM。因为图(a)中共有四个像素等级,所以GLCM是一个 4 × 4 4\times4 4×4的矩阵,以图©水平方向为例,相邻为(0, 1)的共生点共有2个,相邻(0, 2)的共生点有1个。值得重点解释的是,相邻为(0, 0)的共生点个数为2,但是就像(0,1)!=(1,0)需要分别计算,(0,0)的也应该被计算两次,所以(0,0)的共生点为4,(2,2)的共生点为6。
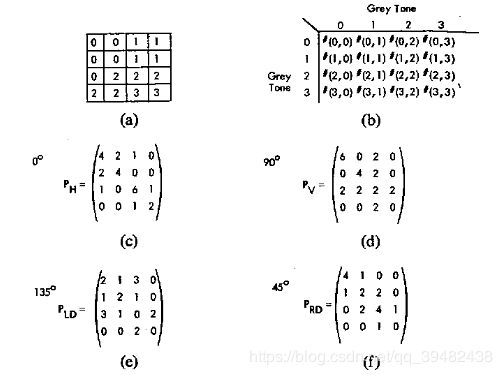
特点: 当色素值分布均匀时,矩阵值分布在主对角线附近;当色素值相差较大时,矩阵值分布原理主对角线。
2. GLCM计算得到的纹理特征
设i,j 分别是(x, y), (x+d, x+l)的像素值,(i,j)的个数为 N ( i , j ) N_{(i,j)} N(i,j),GLCM中所有值之和 N G L C M N_{GLCM} NGLCM,则定义 P ( i , j ) = N ( i , j ) N G L C M P(i, j) = \frac{N_{(i,j)}}{N_{GLCM}} P(i,j)=NGLCMN(i,j) 这里使用频率估计概率,P(i, j)就是(i, j)在图像中出现的概率。
对比度(contrast): 像素的空间分布越不均匀,表现为纹理越深,其对比度就越大,视觉效果就越清晰。
C O N = ∑ i ∑ j ( i − j ) 2 P ( i , j ) CON = \sum_i \sum_j (i-j)^2P(i,j) CON=i∑j∑(i−j)2P(i,j)
逆差矩(inverse different moment): 反应图像纹理的同质性,度量图像纹理局部变化的多少。其值越大说明图像的不同区域间缺少变化。
I D M = ∑ i ∑ j P ( i , j ) 1 + ( i − j ) 2 IDM=\sum_i \sum_j \frac{P(i,j)}{1+(i-j)^2} IDM=i∑j∑1+(i−j)2P(i,j)
熵: 反应图像所具有的信息量,纹理信息也是属于图像的信息,是一个随机性的度量。如果一个图像的随机或噪声越大,熵就会越大。如果一个图像的随机性越大,其共生矩阵中的值之间越相近,此时熵越大。它表示了图像中纹理的复杂程度。 E N T = − ∑ i ∑ j P ( i , j ) log P ( i , j ) ENT = - \sum_i \sum_j P(i,j)\log P(i,j) ENT=−i∑j∑P(i,j)logP(i,j)
能量(angular second moment): 反映了图像中弧度分布的均匀程度和纹理粗细度。如果GLCM中各值集中在一块,则该值越大。
A S M = ∑ i ∑ j ( P ( i , j ) ) 2 ASM=\sum_i \sum_j (P(i,j))^2 ASM=i∑j∑(P(i,j))2
自相关(correlation): 反映了图像纹理的一致性。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。它度量空间灰度共生矩阵在行或列或特定角度方向上的相似程度。
C O R = ∑ i ∑ j ( i j ) P ( i , j ) − u i u j s i s j COR = \sum_i \sum_j \frac{(ij)P(i,j)-u_i u_j}{s_is_j} COR=i∑j∑sisj(ij)P(i,j)−uiuj
其中
u i = ∑ i ∑ j i . P ( i , j ) u_i = \sum_i \sum_j i.P(i,j) ui=∑i∑ji.P(i,j),
u j = ∑ i ∑ j j . P ( i , j ) u_j = \sum_i \sum_j j.P(i,j) uj=∑i∑jj.P(i,j),
s i 2 = ∑ i ∑ j P ( i , j ) ( i − u i ) 2 s_i^2 = \sum_i \sum_j P(i,j)(i-u_i)^2 si2=∑i∑jP(i,j)(i−ui)2,
s j 2 = ∑ i ∑ j p ( i , j ) ( j − u j ) 2 s_j^2 = \sum_i \sum_j p(i,j)(j-u_j)^2 sj2=∑i∑jp(i,j)(j−uj)2
!建议您同时阅读
《纹理特征二:GLRLM–灰度行程矩阵》
《纹理特征三:GLSZM–灰度区域大小矩阵》
《纹理特征四:NGTDM–邻域灰度差矩阵》
参考文献:A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities