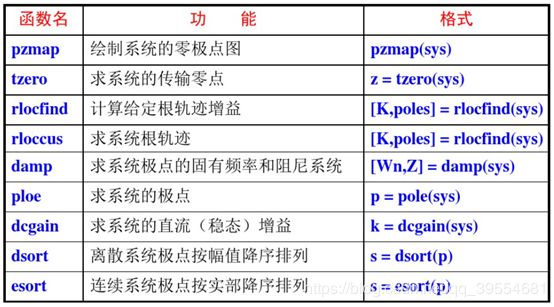
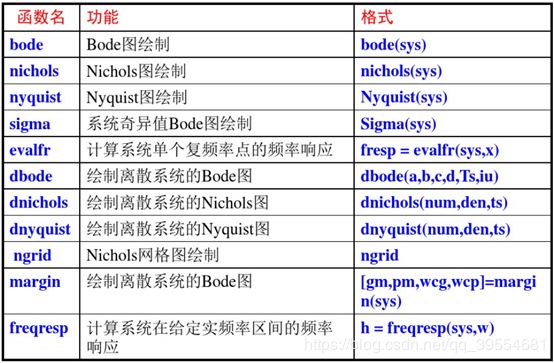
自动控制原理中常用的MATLAB指令
建立控制系统的模型
tf(num,den,…); 生成传递函数模型;
zpk(z,p,k,…); 生成零极点增益模型;
ss(a,b,c,d,…); 生成状态空间模型;
sys=series(SA,SB); 两个环节级联
sys=parallel(SA,SB); 两个环节并联
S=feedback(SA,SB); A环节前向,B环节反馈
[num,den]=ss2tf(A,B,C,D); 状态空间方程转传递函数
[A,B,C,D]=tf2ss(num,den); 传递函数转状态空间方程
控制系统的时域分析
[u,t]=gensig(‘type’,tau); 按照指定的类型 t y p e type type和周期 t a u tau tau生成特定类型的激励信号 u u u,其中 t y p e type type可以选择 s i n sin sin(正弦)、 s q u a r e square square(方波)、 p u l s e pulse pulse(脉冲);
impulse(sys);单位脉冲响应
step(sys);单位阶跃响应
lsim(sys,u,T);LTI模型的任意输入响应函数,计算线性时不变系统 s y s sys sys在任意输入 u u u持续时间 T T T的作用下的输出 y y y,只返回图形。
简单的使用方法如下
[u,t]=gensig(‘square’,6,12,0.1);
plot(t,u,’-.’);hold on;
sys=tf([1 1],[1 2 5]);
lsim(sys,u,t)
控制系统的根轨迹
控制系统的频域分析
重要
sisotool 工具箱可以对单输入单输出系统进行校正装置设计,非常强大的一点在于可以随意设置校正装置零极点并实时观察校正后系统的开环波德图,用来做频域的一些超前、滞后等校正装置十分方便。
控制系统的状态空间分析
可控性分析
Co=ctrb(sys); 或Co=ctrb(A,B);
求系统的可控性矩阵Co,若Co满秩则系统可控
可观性分析
Ob=obsv(sys); 或Ob=obsv(A,C);
求系统的可观性矩阵Ob,若Ob满秩则系统可观
通用相似变换函数ss2ss()
syst=ss2ss(sys,T);
通过非奇异变换矩阵 T T T,把状态变量 x x x变成 z = T x z=Tx z=Tx,变换后的状态空间模型 s y s t syst syst为:
z ˙ = [ T A T − 1 ] z + [ T B ] u \dot z=\left[T A T^{-1}\right] z+[T B] u z˙=[TAT−1]z+[TB]u
y = [ C T − 1 ] z + D u y=\left[C T^{-1}\right] z+D u y=[CT−1]z+Du
变为规范形式的函数canon()
csys=canon(sys,type)
用来把系统 s y s sys sys变为规范形式 c s y s csys csys。 t y p e type type用来选择规范的类型,由两种可选形式: ′ m o d e l ′ 'model' ′model′约当矩阵形式和 ′ c o m p a n i o n ′ 'companion' ′companion′伴随矩阵形式。
可控性分解
[Abar,Bbar,Cbar,T,k]=ctrbf(A,B,C)
把系统分解可控和不可控两部分。
可观性分解
[Abar,Bbar,Cbar,T,k]=obsvf(A,B,C)
把系统分解为可观和不可观两部分。
其他
连续系统的lqr控制器设计
lqr(A,B,Q,R)
待补充。。。
参考文档地址