机器学习与数学基础知识(一)
最近,朋友分享给我一套“七月在线”的机器学习视频,我几经思量之后,决定从视频量最少的数学基础部分开始看起,今天学习完了第一个视频,长达2小时,感觉老师讲的挺不错的。以前自己就对机器学习很感兴趣,做了一些了解和尝试性地学习,也看了一点经典的林轩田和吴恩达系列的视频,个人觉得再经典的机器学习视频也需要一个良好的数学基础来入门。
第一集的视频主要是系统介绍了机器学习基础与相关数学基础的一些概念,具体的内容会在以后的视频中展开。
一 机器学习基础
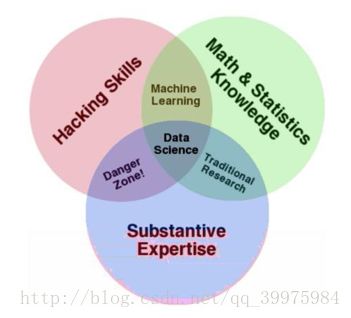
这是一张解释 计算机编程能力(左上),个人专业领域(下面)和数学统计学知识(右上)关系的图片。对于个人专业领域,是你从事的某一方向或者专业,比如图像处理,数据挖掘,语音识别等这些可以用到机器学习的领域;在当今AI的大趋势下,很多人都想转型到AI的领域分一杯羹,那么这些人大多是个人专业领域很强和编程能力很强的结合体,属于危险区域(Danger Zone),你可以直接使用机器学习的模型,简单的带入数据,让程序跑起来,解决工程问题,但是仅限于简单的机器学习算法,稍微复杂的机器学习算法,必然要以强大的数学基础为支撑,来保证你正确使用,维护和优化机器学习算法。如果你个人专业领域很强,而且数学基础也很棒,但缺乏代码能力,那么你很适合做一个研究者,去研究和开发机器学习算法,不必做过多的工程实践,类似专硕研究生和博士的区别一样。总的来说,数学统计学基础尤为重要,打好数学基础,有助于你更好的入门机器学习。
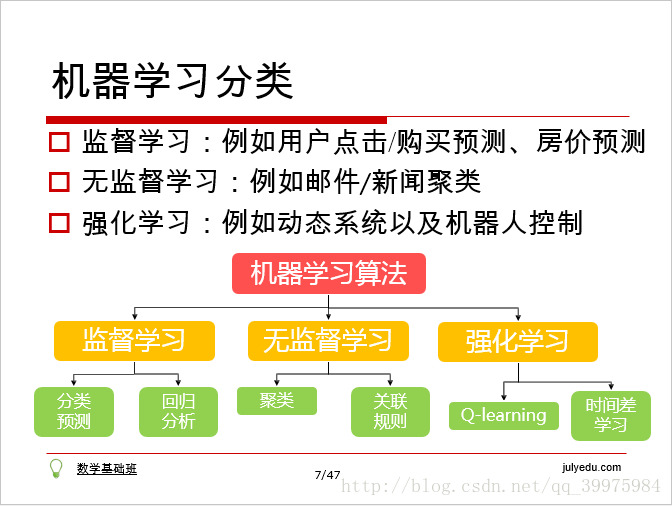
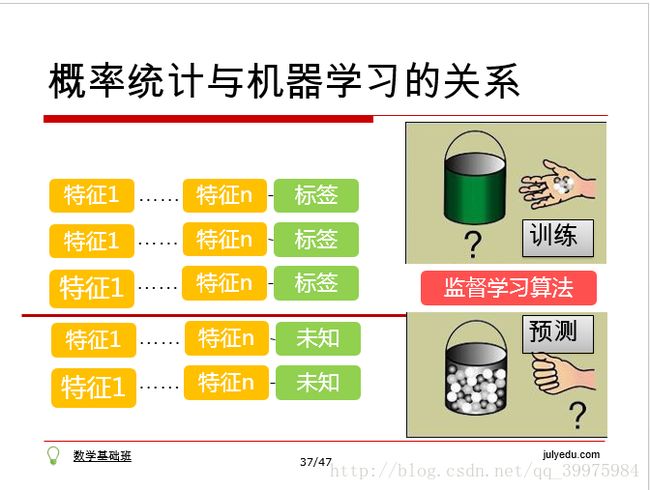
这张图片为机器学习算法的分类,这里简单提一下监督学习和无监督学习。大家都知道,机器学习算法就跟人的大脑一样,人的大脑基于观察形成经验对事情做出判断,机器学习基于数据(样本)形成模型对目标(标签)做出预测;那么,样本分为两类,一类为目标已知的数据(样本),一类是目标未知的数据(样本),基于前者形成的模型是监督学习,基于后者的是无监督学习。(因为本文重点在于阐明机器学习中的数学基础,对于机器学习的概念不作详细介绍,这部分目的是要你知道数学对机器学习的重要性)
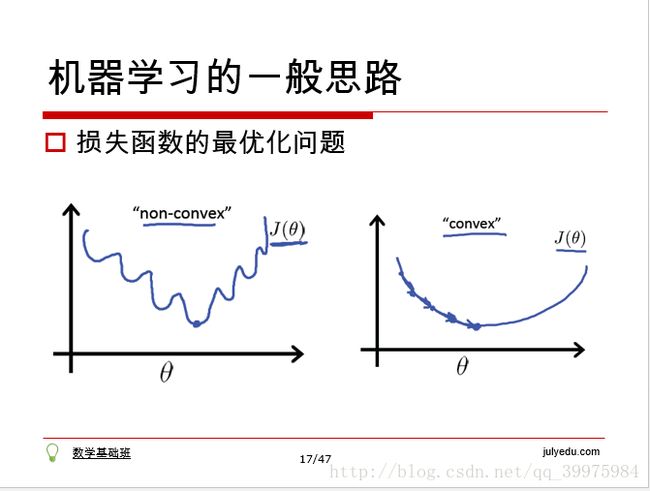
这个是第一部分“机器学习基础”的重点——机器学习的一般思路。举例:凤姐的女儿去和100个男人相亲,凤姐根据高,富,帅,潜,德共五方面(可以理解为自变量)来决定其成为自己女婿的概率(可以理解为因变量)。根据这五方面在凤姐心中的重要性,凤姐会选择权重w1,w2,w3,w4,w5列出一个得分函数z。而这些权重值w1,w2,w3,w4,w5是由损失函数(图中给出了两种损失函数模型,非凸函数和凸函数)得出的,即损失函数的最优化问题,这里可以将损失函数的横坐标理解为(w1,w2,w3,w4,w5)组成的向量,最优化的解即为损失函数纵坐标取最小值时对应的横坐标(w1,w2,w3,w4,w5),这样就找到了得分函数z,即该问题的机器学习算法模型。
二 微积分基础
这部分作者只是提到了一些微积分中比较重要的概念及其几何意义,并未具体展开进行讲解,相信大家在本科阶段都学过高数,并且掌握了其知识点,那么我这里做一个分条整理:
1 夹逼准则:用来求极限的一种方法。
2 导数:一阶导数表示曲线变化的快慢,即斜率,二阶导数表示斜率变化的快慢,即凹凸性。
3 方向导数:标量;可以类比一阶导数理解,只不过不是对x方向的求导,而是对某一方向的求导。
4 梯度:矢量;模值表示方向导数的最大值,方向表示方向导数取最大值时的方向。
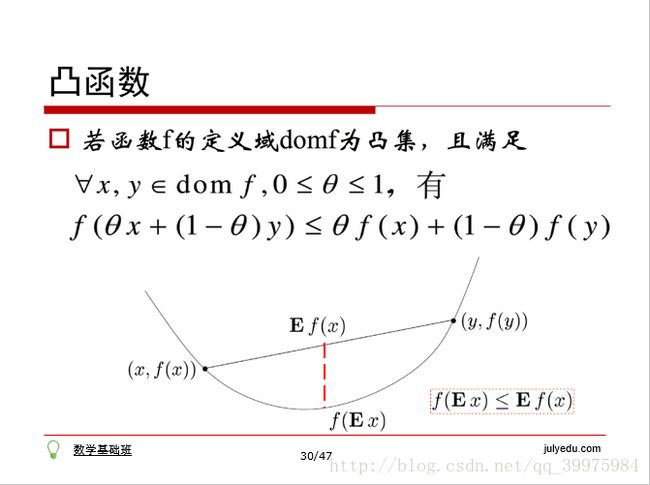
5 凸函数:Jensen不等式f[E(x)]<=E[f(x)]要理解。
下面贴出梯度和凸函数的图片,梯度图片中,最下面有一个“梯度下降法”,主要用在损失函数的最优化中;凸函数图中,标出了Jensen不等式的几何意义,有助于大家理解。
三 概率与统计基础
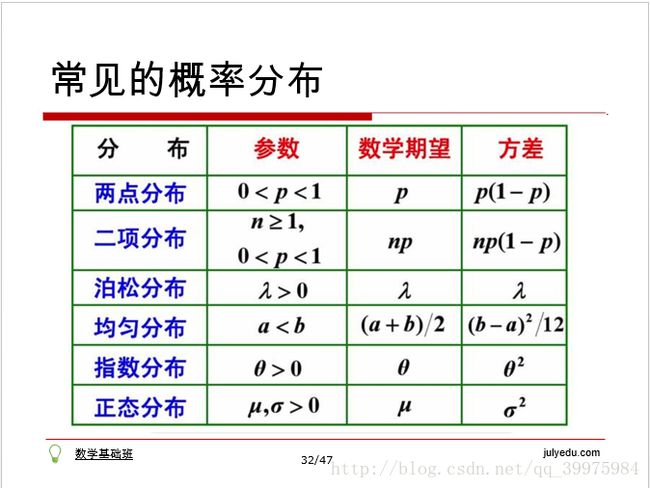
这部分的知识点适合以图片的方式呈现(大家注意区分概率,统计是两个概念)。