二分图
文章目录
- 二分图
- 一. 二分图的判断
- 二.二分图的最大匹配
- 三. 二分图最小点覆盖和最大独立集
- 四. 二分图的最大权匹配
二分图
二分图又称作二部图, 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。通俗来讲,就是二分图中的每一条边的两个顶点,应属于不同的顶点集合。
一. 二分图的判断
如果存在一条边的两个顶点属于同一个集合,则这个图就不是二分图。可以使用红黑染色法进行判断,每个顶点染成红色或者黑色,如果存在一个方案使得图中的每一条边的两个顶点染上不同的颜色,则该图为二分图。染色的算法为:
- 选取一个未染色的点u进行染色
- 遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并对v重复第2步;若v已经染色,如果 u和v颜色相同,判定不可行退出遍历。
- 若所有节点均已染色,则判定可行。
const int maxn = 100010;
const int INF = int(1e9);
int n, m;
int x[maxn], y[maxn];
int vis[maxn];
vector<int>stu[maxn];
int dfs(int a,int b) {
vis[a] = b;
for (int i = 0; i < stu[a].size(); i++) {
if (vis[stu[a][i]] ==0) {
//vis[stu[a][i]] = -b;
if (dfs(stu[a][i], -b) == 0)
return 0;
} else {
if (vis[stu[a][i]] == b)
return 0;
}
}
return 1;
}
int main() {
int a, b;
int Case;
scanf("%d",&Case);
while (Case--) {
scanf("%d%d", &n, &m);
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n; i++)
stu[i].clear();
for (int i = 1; i <= m; i++) {
scanf("%d%d", &a, &b);
stu[a].push_back(b);
stu[b].push_back(a);
}
bool flag=true;
for(int i=1; i<=n; i++) {
if(vis[i]==0) {
if(dfs(i,1))
continue;
flag=false;
break;
}
}
if (flag)
printf("Correct\n");
else
printf("Wrong\n");
}
return 0;
}
二.二分图的最大匹配
一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
二分图的最大匹配使用的是匈牙利算法
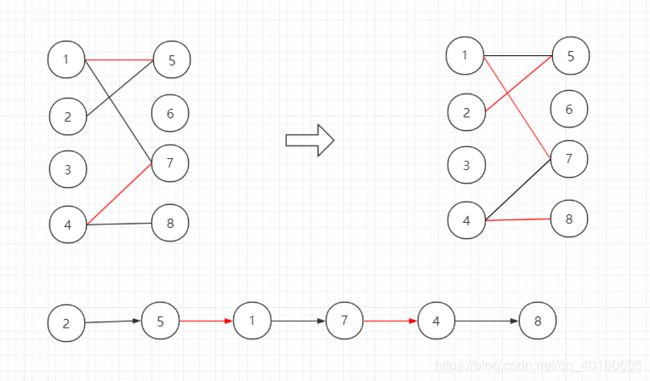
交替路:如果从一个未匹配点出发,经过未匹配边,匹配边,未匹配边…匹配边,未匹配边这样的路径,则称为交替路。如下图所示:路径2->5->1->7就是一条交替路。
增广路:如果从一个未匹配点出发,走交替路能到达一个未匹配点,则称为增广路。这时候,匹配边变成未匹配边,未匹配边变成匹配边,匹配边就比原来的多出一条,所以叫做增广路。如下图所示:路径2->5->1->7->4->8就是一条增广路。
-
依次枚举每一个点i;
-
若点i尚未匹配,则以此点为起点查询一次交错路径。若存在交替路径,将该交错路径的匹配边和未匹配边交换。
const int maxn = 1010; const int INF = int(1e9); int n, m; int maps[maxn][maxn]; //用来标记结点之间是否有关系 int x[maxn], y[maxn]; //所有的结点分成两部分,x[]用来记录x部分结点对应的y[]部分的结点 int vis[maxn]; //用来标记该结点是否已经查找过 vector<int>stu[maxn]; int path(int u) //增广路查找 { for (int i = 1; i <= n; i++) { if (maps[u][i] == 1 && vis[i] == 0) { vis[i] = 1; //标记该结点查找过 if (y[i] == -1 || path(y[i])) //回溯 { x[u] = i; //增广路查找成功,记录路径 y[i] = u; return 1; } } } return 0; } int Maxpath() //最大匹配 { int ans = 0; memset(x, -1, sizeof(x)); memset(y, -1, sizeof(y)); for (int i = 1; i <= n; i++) { if (x[i] == -1) //未匹配的结点 { memset(vis, 0, sizeof(vis)); //初始化所有的标记 ans += path(i); } } return ans; //返回最大匹配 } int main() { int a, b; while (~scanf("%d%d", &n, &m)) { memset(maps, 0, sizeof(maps)); //初始化maps[][]各结点的关系 memset(vis, 0, sizeof(vis)); //初始化标记数组 for (int i = 1; i <= n; i++) stu[i].clear(); for (int i = 1; i <= m; i++) { scanf("%d%d", &a, &b); stu[a].push_back(b); stu[b].push_back(a); maps[a][b] = maps[b][a] = 1; } int sum = Maxpath(); printf("%d\n", sum / 2); /*for (int i = 1; i <= n; i++) cout << i << " " << x[i] << endl;*/ } return 0; }
三. 二分图最小点覆盖和最大独立集
最小点覆盖:在图G中选取尽可能少的点,使得图中每一条边至少有一个端点被选中。
结论:由König定理可知最小点覆盖的点数 = 二分图最大匹配
最大独立集:在图G中选取尽可能多的点,使得任意两个点之间没有连边。
结论:最大独立集的点数 = 总点数 - 二分图最大匹配
四. 二分图的最大权匹配
二分图的最大权匹配可以用Kuhn-Munkres算法解决。
(等有空再把这个坑补上,下面直接上模板)
输入数据包含多组测试用例,每组数据的第一行输入n,表示房子的数量(也是老百姓家的数量),接下来有n行,每行n个数表示第i个村民对第j间房出的价格(n<=300)。 问题就是村领导怎样分配房子才能使收入最大.,对每组数据输出最大的收入值,每组的输出占一行。
#include
#include
#include 参考资料:http://hihocoder.com/problemset中的二分图题目