信息安全数学基础(初等数论)第三章有限域速览

定理3.1

设是一个域，那么，
(1) 对于任意 ∈ ，0 = 0 = 0；
(2) 任意， ∈ ，若 = 0，则 = 0或 = 0。

定理3.2

设₀是域的非空子集，当且仅当以下条件成立时₀是域的子域：
(1) 任意， ∈ ₀，都有−， + ∈ ₀；
(2) 任意非零元素， ∈ ₀，都有⁻¹， ∈ ₀。

定理3.3

设是一个域，， ∈ ，则对于任意正整数，$(a+b{)}^n={\sum }_{i=0}^n\left(\begin{array}{l}n\\ i\end{array}\right)a^{n-i}{b}^i$。

定理3.4

设是一个域，如果ℎ()¹为正整数，则必为某个素数。 特征为素数的域的素域²与ℤ同构，特征为0的域的素域与ℚ同构。

定理3.5

设是一个域， ℎ() = ，则对于任意， ∈ ， ≥ 0，均有
$(a\pm b{)}^{p^n}=a^{p^n}\pm b^{p^n}$；
若() ，()是特征为的域上的多项式，那么
$(f(x)\pm g(x){)}^{p^n}=f(x{)}^{p^n}\pm g(x{)}^{p^n}$。

定理3.6

设()，()为域上的两个多项式，() ≠ 0，则存在唯一的一对多项式()，()，使得：
() = ()() + ()， () < ()；
()称为()被()除所得的余式，记作$(f(x){)}_{g(x)}=r(x)$。

定理3.7

设₁()，₂()，()为域上的多项式，() ≠ 0，则
${\left(f_1(x)+f_2(x)\right)}_{g(x)}={\left(f_1(x)\right)}_{g(x)}+{\left(f_2(x)\right)}_{g(x)}$
${\left(f_1(x)f_2(x)\right)}_{g(x)}={\left({\left(f_1(x)\right)}_{g(x)}{\left(f_2(x)\right)}_{g(x)}\right)}_{g(x)}$

定理3.8

域上的多项式()是可约多项式，当且仅当存在两个域上的多项式₁()，₂()， ₁( ) < ()， ₂( ) < ()， 使 得() =₁()₂()。

定理3.9

域上的多项式() | ₁()，() | ₂()，那么对于上的任意多项式(),()，有() | ()₁() + ()₂()

定理3.10（欧几里得辗转相除法）

设0()，1()为域上的两个多项式，1() ≠0，则可得如下带余除法算式：
₀₍) = ₁()₁() + ₂()， 0 ≤ ₂( ) < ₁( )
₁() = ₂()₂() + ₃()， 0 ≤ ₃( ) < ₂( )
… …
₋₂() = ₋₁()₋₁() + ()， 0 ≤ ( ) < ₋₁( )
₋₁() = ()() + ₊₁()， ₊₁() = 0
经过有限步后，余式必然为0；
存在多项式()，() ∈ []，使得()₀() + ()₁() = ()；
设()首项系数为，则(₀() , ₁()) = ⁻¹()，且最高公因式是唯一存在的。
对任意() ∈ []，若() | ₀()，() | ₁() ，那么() | (₀(), ₁())。

定理3.11

设()，()为域上两个不全为零的多项式，则对于任意() ∈ []，(() + ()() , ()) = (() , ())。

定理3.12

设 ()，₁()，₂() 为 域 上的多项式 ， 且() | ₁()₂()，若(() , ₁()) = 1，则() | ₂()。

定理3.13

设()，₁()，₂()为域上的多项式，()为域上的不可约多项式，且()|₁()₂()，则()|₁()或()|₂()。

推论
设()，()为域上两个次数大于0的多项式，那么，存在唯一的一对多项式()，() ∈ []，使得()() + ()() = ((), ())，且
() < () − ((), ());
() < () − ((), ())。

定理3.14（唯一因式分解定理）

设()是域上次数大于0的多项式，则()
可以唯一地表示为域上一些次数大于0的不可约多项式的乘积。 特别地，
设()是首1多项式，且，
() = ₁()₂() ⋯ () = ₁()₂() ⋯ ()，
其中₁()，₂()， ⋯ ，()，₁()，₂()， ⋯ ，()均为域上次数大于0的首1不可约多项式，则 = ，经过适当的调整可使₁() = ₁()，₂() = ₂()， ⋯ ，() = ()。

定理3.15（余元定理）

设()为域上的多项式，对于任意 ∈ ，存在() ∈ []使得
() = ( − )() + ()

推论1
设()为域上的多项式，为()在域中的根的充要条件是( − ) | ()。
推论2
设()为域上的 ≥ 1次多项式，如果₁，₂， ⋯ ，为()在域中的 ≥ 1个不同的根，则存在 − 次多项式() ∈ []使得，
() = ( − ₁)( − ₂) ⋯ ( − )()。
推论3
设()为域上的 ≥ 1次多项式，则()在的任意扩域中，不同根的个数都不会超过。

定理3.16（扩域的构造）

设()为域上的 ≥ 1次不可约多项式，集合$\mathbb{F}[x{]}_{f(x)}=\left\{{\sum }_{i=0}^{n-1}{a}_i{x}^i|a_i\in \mathbb{F}\right\}$按照模()的模加和模乘形成一个域。 特别地，若()为有限域上的次不可约多项式， 则${\mathbb{F}}_q[x{]}_{f(x)}=\left\{{\sum }_{i=0}^{n-1}{a}_i{x}^i|a_i\in {\mathbb{F}}_q\right\}$按照模()的模加和模乘形成一个元素个数为的有限域。

定理3.17

设()是域上的一个次数大于0的不可约多项式，那么()必然在的某个扩域中有根。
推论
上的任意一个次数为 ≥ 1的多项式，必然在的某个扩域中可以分解为个一次不可约多项式的乘积。

定理3.18

设是有限域，是其元子域，则存在正整数，使得|| = ⁿ。
推论1
有限域的元素个数必为，其中为素数，为正整数。
推论2
任何有限域都是其素域的扩域。

定理3.19

设是元有限域，是的扩域， ∈ ，那么是多项式 − 的根当且仅当 ∈ 。
批注
由定理3.19，元素个数为的有限域，可以看成恰好是由多项式 − 的个根组成。

定理3.20

设为元有限域，() ∈ []为( ≥ 1)次不可约多项式，那么 $f(x)|x^{q^n}-x$。

定理3.21

设, 为正整数，那么( − 1, − 1) = ^(,) − 1。
推论
设, , 为正整数，那么$\left(x^{q^m}-x,x^{q^n}-x\right)=x^{q^{(m,n)}}-x$。

定理3.22

设为元域，为正整数，() ∈ []为次不可约多项式，且 > ，那么$f(x)\nmid x^{q^n}-x$。

定理3.23

设为元域，, 为正整数，() ∈ []为次不可约多项式，那么$f(x)\nmid x^{q^n}-x$，当且仅当|。

定理3.24

设为元有限域，()， () ∈ []，若()是()的重因式，则()⁻¹ | ′()。
推论1
设为元域，() ∈ []，若((), ′()) = 1，则()在域上没有重因式，也没有重根。
推论2
设为元域，为正整数，那么$f(x)\nmid x^{q^n}-x$在域上没有重因式。

定理3.25

设为元域，为正整数，那么上一定存在次不可约多项式。

定理3.26

对于任意素数，正整数，元有限域一定存在。

引理1

设群中元素的阶为，则对于任意整数，$\mathrm{ord}\left({\alpha }^m\right)=\frac{n}{(m,n)}$。

引理2

设群中ord() = ，ord() = ，若(, ) = 1，则ord() = 。

定理3.27

有限域的乘法群是循环群。

定理3.28

元素个数相等的有限域是同构的。

定理3.29

若< >是由生成的阶循环群，则：
(1) < >的子群都是循环群；
(2)对于任意正整数|， < >存在唯一的元子群；
(3)若整数,不全为0，则< , > = < ^(,) >。

引理3

设是元素个数为的有限域，有限域为其扩域，中的任一元素在上的极小多项式存在且唯一。
推论
在上的极小多项式也是上以为根的首项系数为1的次数最低的多项式。

定理3.30

(1) 设() ∈ 是一个次不可约多项式，那么包含()的根的最小扩域为${\mathbb{F}}_{q^n}$，所有包含()的根的域都是${\mathbb{F}}_{q^n}$ 的扩域。
(2) 是元有限域，那么其扩域 ${\mathbb{F}}_{q^n}$中包含所有次数为的因子的不可约多项式的所有根，而不包含次数不为的因子的不可约多项式的任何根。

引理4

设是元素个数为的有限域，有限域为其扩域， ∈ ^∗，的阶为，设是最小的使得 ≡ 1( )的正整数，则在上的极小多项式为次，该多项式的个根为$\alpha ,{\alpha }^q,{\alpha }^{q^2},\cdots ,{\alpha }^{q^{k-1}}$。进一步，若|| = ，是的本原元，则在上的极小多项式一定是次的。
推论
设是元素个数为的有限域，()为上的( ≥ 1)次不可约多项式，${\mathbb{F}}_{q^n}$为的任一扩域，那么()在${\mathbb{F}}_{q^n}$中有根，且若是()在${\mathbb{F}}_{q^n}$中的一个根，那么()在${\mathbb{F}}_{q^n}$中的所有根为$\alpha ,{\alpha }^q,{\alpha }^{q^2},\cdots ,{\alpha }^{q^{n-1}}$。

定理3.31（伽罗华定理）

设 p 为素数，${\mathbb{F}}_{q^n}$是元素个数为的有限域，是其一个n次本原多项式()的根，则：
（1）${\mathbb{F}}_{q^n}$的任意自同构都保持其子域中的元素不变；
（2）${\mathbb{F}}_{q^n}$的任意自同构都只能将()的根映射成()的根，由此说明，任意自同构，都满足$\delta (\alpha )={\alpha }^{p^i},i=0,1,2,\dots ,n-1$；
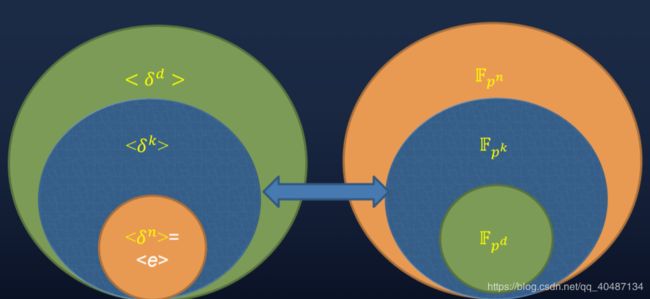
（3）设() = ，则${\mathbb{F}}_{q^n}$的所有自同构可以表示为， = 0,1,2, … , − 1是由 生成的一个 n 阶循环群 <>， 保持不变的所有元素形成子域${\mathbb{F}}_{q^{(n,i)}}$，所有保持${\mathbb{F}}_{q^{(n,i)}}$中的元素不变的自同构形成子群<>＝ <^(,)>，简言之，(, ) = |，保持${\mathbb{F}}_{q^d}$中的元素不变的自同构形成子群<>。
（4）一般地，对于d|n，保持子域${\mathbb{F}}_{q^d}$中的元素不变的所有${\mathbb{F}}_{q^n}$上的自同构形成循环群<>，称为扩张${\mathbb{F}}_{p^n}/{\mathbb{F}}_{p^d}$的伽罗华群，记作Gal(${\mathbb{F}}_{p^n}/{\mathbb{F}}_{p^d}$)，对于任意d|k，k|n，中间域${\mathbb{F}}_{q^k}$扩张的伽罗华群Gal($={\mathbb{F}}_{p^n}/{\mathbb{F}}_{p^k}$)是Gal(${\mathbb{F}}_{p^n}/{\mathbb{F}}_{p^d}$)的子群<>，反之Gal(${\mathbb{F}}_{p^n}/{\mathbb{F}}_{p^d}$)的任意子群保持不变的所有元素是${\mathbb{F}}_{q^n}$和${\mathbb{F}}_{q^d}$的中间域，Gal(${\mathbb{F}}_{p^n}/{\mathbb{F}}_{p^d}$)的子群和中间域之间一 一对应。

---

1. 域 的特征 ↩︎

2. 最小子域 ↩︎