Python学习之---杨辉三角的五种解法

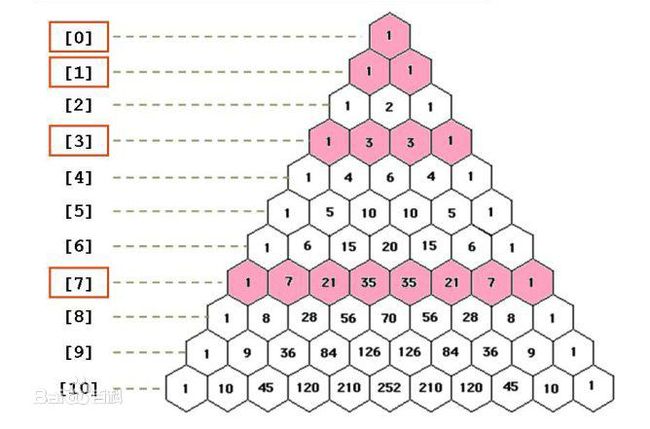
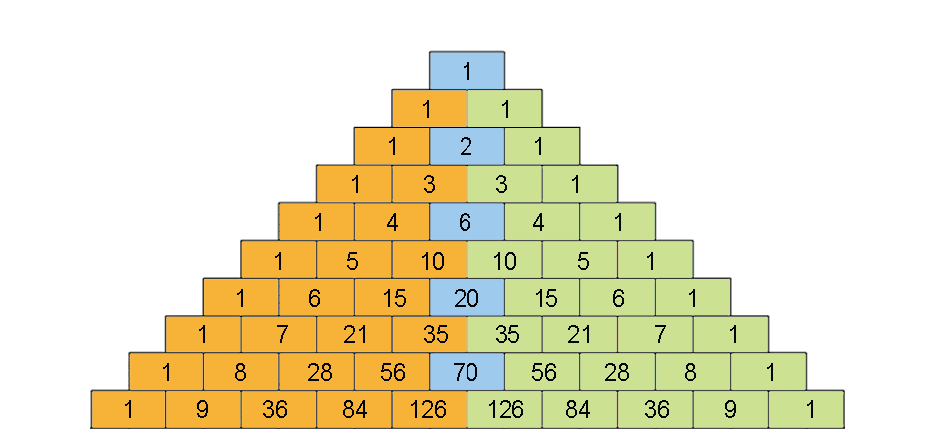
杨辉三角（也称帕斯卡三角）对与编程初学者来说,肯定不陌生，它是一个无限对称的数字金字塔，从顶部的单个1开始，下面一行中的每个数字都是上面两个数字的和。

杨辉三角，是二项式系数在三角形中的一种几何排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623—-1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。
那么什么是杨辉三角呢?
啥也不多说,

小二,上图!!!

虽然不同的编程语言对于杨辉三角的求解方式不一样,但是,求解思路大致相同.今天我们先来讨论python初学者对杨辉三角的几种求解方法,等后期学习了更高级的函数,在进行补充.

知识储备需求:
python初学者,了解python中循环与列表基础知识.

方法一:基本法

#解释:将所有元素添加到一个列表中,最后一次打印出结果
num = 10
triangle= [1,[1,1]]
for i in range(2,num):
    cur=[1]               #定义新列表起始值cur --current
    pre= triangle[i-1]    #提取新行的前列所有元素待用
    for j in range(i-1):  #定义两两相加的界限,即取值最大为i-2
        cur.append(pre[j]+pre[j+1])#依次迭代相加
    cur.append(1)     #尾部插入数字1,比用 insert 方法效率来的高,只是尾部追加,#不用每次插入都向后移动元素,因此insert法虽然可行禁用,效率太低,占据内存较多.
                          
    triangle.append(cur)  #列表中插入新生成的列表
#     cur=[1]
#     for j in range(0,i-1):
#         cur.append(triangle[i-1][j]+triangle[i-1][j+1])
#     cur.append(1)
#     triangle.append(cur)
#     print(cur)            #(比较注释行,两种方法结果相同,操作稍有变化,都是索引列表,还有就是打印时是一行打印还是)
    
                            
print(triangle)           #打印出结果
    
#优化代码打印,去除特例行:
num = 10
for i in range(num):
    cur=[1]               #定义新列表起始值cur --current
    triangle.append(cur)  #起始追加,列表存放索引地址,当后面进行cur.append()后,这里因为地址索引没变,但内部值发生了改变   
    if i ==0:
        continue
    pre= triangle[i-1]    #提取新行的前列所有元素待用
    for j in range(i-1):  #定义两两相加的界限,即取值最大为i-2
        cur.append(pre[j]+pre[j+1])#依次叠加
    cur.append(1)     #尾部插入数字1,比用 insert 方法效率来的高,只是尾部追加,
                          #不用每次插入都向后移动元素,因此insert法虽然可行禁用,效率太低,占据内存较多.
print(triangle)          

方法二:补零法

#解释:除第一行外,尾部加一个0,在后续计算最后一个数1时,可以由上一行补的0相加而得,就可以不使用额外的append(1),但并没有提高效率,仅作为解法之一
n= 10
triangle = [[1],[1,1]]
for i in range (2,n):
	newrow = triangle[i-1]
	newrow.append(0)   #尾部追加一个0
	row=[None]*(i+1)   #创建空列表,一次性开辟所需内存.
	for j in range(i+1):
		row[j]=newrow[j-1]+newrow[j]
	triangle.append(row)
print(triangle)
# 下面方法同样是使用了补零法,但是过程新建了新列表,这样结果不会出现无用数字0
# n= 10
# newline= [1]
# print(newline)
# for i in range(1,n):
#     oldline = newline.copy()
#     oldline.append(0)
#     newline.clear()    #清理数据,最后会出现大量的内存垃圾.
#     for j in range(i+1):
#         newline.append(oldline[j-1]+oldline[j])
#     print(newline)  

方法三 对称法

#解释:观察杨辉三角,可以看出杨辉三角是关于Y轴对称的,因此可以利用对称性,只需要计算左边的数据即可,右边部分只需镜像左边即可
#数据镜像可以通过正向索引和负数索引得到.  
n =10
triangle = [1,[1,1]]
for i in range(2,n):
    cur=[1]*(i+1)
    pre= triangle[i-1]    
    for j in range(1,i//2+1):
        cur[j]=triangle[i-1][j-1]+triangle[i-1][j]
        if i !=2*j:
            cur[-j-1]=cur[j]#  过滤"中点"重复计算.例如值为中间值为2,6,...
    triangle.append(cur)
print(triangle)

##中点的另一种求解  
n =10
triangle = [1,[1,1]]
for i in range(2,n):
    cur=[1]*(i+1)
    pre= triangle[i-1]    
    for j in range(i//2):
        cur[j+1]=triangle[i-1][j]+triangle[i-1][j+1]
        cur[-j-2]=cur[j+1]#  过滤"中点"重复计算.例如值为中间值为2,6,...
    triangle.append(cur)
print(triangle)   

方法四 :单行覆盖

#解释:单个列表,切片完成
n =10
triangle=[1]*n  #一次开辟所有内存空间
for i in range(n):
    for j in range(i//2):
        triangle[j+1]= triangle[j]+triangle[j+1]
              
        triangle[i-j-1]=triangle[j+1]    #已经开辟了所以空间,负索引使用的是末尾的元素,所以不能用负索引,可以使用正索引    
                                       #运行中出现问题,例如第5行结果会出现1,4,7,4,1  其实在运行时,每运行一次,
                                        #内存中的数已经被修改,并不是原先的元素,故,以此操作会迭代相加,导致结果出差.
    print(triangle[:i+1])
    
## 解决方法:
for i in range(n):
    old = 1  #triangle[0]
    for j in range(i//2):            #添加一个中间变量,用于保存上一次运行的结果,使其不被新的数值替换
        tmp = old+triangle[j+1]
        old = triangle[j+1]
        triangle[j+1]= tmp  
        if i !=2*(j+1):
            triangle[i-j-1]=triangle[j+1] #tmp   #与前面一样,排除对称轴旁只出现一次的数
    print(triangle[:i+1])

方法五:组合数公式法

#解释:杨辉三角的任意元素可以根据杨辉三角的性子---组合数公式C(n,m)得到.
#此方法简单的使用的函数调用,和输出格式化,以上四种方法同样可以进行简单的变化,使其更加通用和输出的结果更加美观,读着可以根据自己需要进行相应调整.
Fn=1
Fm=1
Fmn=1

def C(n,m):       #将求组合数封装成函数,这样每次运算时直接调用即可,可以省下循环.

	Fn = 1
	Fm = 1
	Fmn = 1
	# global Fn,Fm,Fmn
	for i in range(1,n):#求n阶乘
		Fn*=i
	for j in range(1,m):#求m阶乘
		Fm*=j
	for k in range(1,n-m+1):#求(n-m)的阶乘
		Fmn*=k
	C=int(Fn/(Fm*Fmn)) #求解组合数,加int是使其输出为整型格式.
	return C
strinput = input("请输入要打印的N行第M个数,以逗号间隔")#可增加检查代码,判断是否按要求输入,如果不是则提示重新输入,用While循环.

nestrinput= strinput.split(',')#分割字符串,提取输入数字
n= int(nestrinput[0])
m= int(nestrinput[1])
# print(n,m)
print("第{}行第{}个数是{}".format(n,m,C(n,m))) #格式化输出
for i in range(1,n+1):
	strline =""
	for j in range(1,i+1):
		strline+= str(C(i,j))+ "  "

	print("第{}行{:^60}".format(i,strline))

输出的结果如下:

请输入要打印的N行第M个数,以逗号间隔10,6
第10行第6个数是126
第1行                            1                               
第2行                           1  1                             
第3行                         1  2  1                            
第4行                        1  3  3  1                          
第5行                      1  4  6  4  1                         
第6行                    1  5  10  10  5  1                      
第7行                  1  6  15  20  15  6  1                    
第8行                1  7  21  35  35  21  7  1                  
第9行              1  8  28  56  70  56  28  8  1                
第10行           1  9  36  84  126  126  84  36  9  1