基于matla的RSSI测距定位技术性能仿真

RSSI原理

RSSI（Received Signal Strength Indicator）是接收信号的强度指示，它的实现是在反向通道基带接收滤波器之后进行的。

RSSI是射频信号理论术语，主要应用于发射机和接收机之间的距离测量。该方法是依据接收信号能量强度确定距离，对通信信道参数要求较高。其测距理论是：依据无线电波或声波在介质中传输，信号功率是随传播距离衰减的原理。根据信标节点已知信号的发射功率和节点接收的信号功率，通过信号与距离之间的衰减模型，就可以计算出节点间的距离。由于信号传播的过程中，受到距离和障碍物的影响。信号的功率强度随之衰减，间接影响精度。所以要求得到良好的精度，短距离才会体现这一点。
由于信号发射设备和接收设备简单、成本低、低功耗，比较适合无线传感器网络定位机制。针对室内和室外环境，现阶段流行的估计位置技术中，对提高估计位置的准确性方面，也有很多方法。例如由三个非共线锚定器组成，通过非共线信标节点进行位置估计的最小二乘法，以及使用三个以上的信标节点多点定位技术。对于测距方法的进行对比如图所示：

由图可以看出：RSSI的定位技术作为基于Wi-Fi活动的RFID标签，相比于TOA、TDOA、AOA、GPS具有成本低、容易实现等优势。如果室内定位精度要求不高，基于RSSI的定位技术完全可以满足。而且，现阶段对于作为节点的传感器，都能够完成发射测试信号功率的任务。主要进行实验时，节点发送数据包，也获取RSSI的测量值。该定位技术既无需额外硬件，又能完成复杂信息的分析处理，减小通信消费，节约成本，比较适用于无线传感器网络的定位系统。

仿真要求

要求一：RSSI的测量值由对数路径损耗模型产生，为减小波动造成的误差，其值可由多次测量取平均值来得到。
要求二：对数路径损耗模型中的参考距离路径损耗和路径损耗因子可通过参考点相互之间的测量值估计。
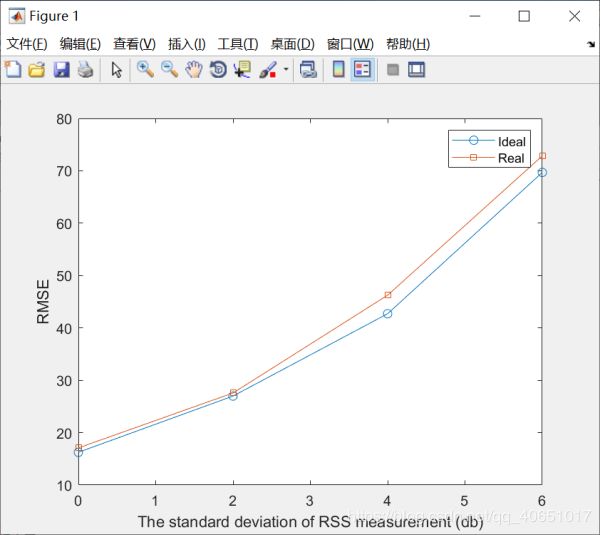
要求三：完成理想情况下（参考距离路径损耗和路径损耗因子已知）与实际情况下的RMSE曲线对比图，横坐标为噪声方差，纵坐标为RMSE。

仿真代码

1.TOALLOP.m

function theta=TOALLOP(A,p,j)
 % A is the coordinate of BSs 
 %A是BBS的坐标
% p is the range measurement 
%P是范围测量
% j is the index of reference BS 
%J是参考BS的索引
[m,~]=size(A);  %size得到A的行列数赋值给[m,~]，~表示占位，就是只要行m的值！
k=sum(A.^2,2);%矩阵A每个元素分别平方，得到新矩阵，在行求和，最为矩阵K
k1=k([1:j-1,j+1:m],:); %取出J行
A1=A([1:j-1,j+1:m],:); %取出J行
A2=A1-ones(m-1,1)*A(j,:); %得到D，就是j行与其余行对应值相减
p1=p([1:j-1,j+1:m],:); %取出J行
p2=p(j).^2*ones(m-1,1)-p1.^2-(k(j)*ones(m-1,1)-k1); %得到b,(Rn*Rn-R1*R1-Kn+K1)其中Kn为对应第n个x^2+y^2
theta=1/2*inv(A2'*A2)*A2'*p2; %利用最小二乘解，得
theta=theta';%转换为（x,y）形式

2.Parameter_est.m

function [pd0_est,n_est]=parameter_est(A,sigma) 
% A is the coordinate of BSs 
% sigma is the standard deviation of RSSI measurement 
[m,~]=size(A); 
pd0=0;
n=3; 
d=zeros(m,m); 
tt=5; 
% the number of RSSI measurement for each BS 
sigma1=10^(sigma/10); 
h1=[];
G1=[]; 
for i=1:m 
    for j=1:m 
        if i~=j 
           d(i,j)=norm(A(i,:)-A(j,:));
           for k=1:tt 
               prd(k)=pd0-10*n*log10(d(i,j))-sigma1*randn; 
           end 
           RSSI=mean(prd);
           d_distance=-10*log10(d(i,j)); 
           h1=[h1;RSSI];
           G1=[G1;d_distance]; 
        end
     end
end
h=h1;
[m1,~]=size(h); 
G=[ones(m1,1),G1];
x=inv(G'*G)*G'*h; 
pd0_est=x(1,1);
n_est=x(2,1);
end

3.RSSImain.m

% %% the simulation of RSSI localization algorithm 
clear all; 
clc; 
BS1=[0,0];
BS2=[500,0];
BS3=[500,500];
BS4=[0,500]; 
MS=[100,100]; 
std_var=[0,2,4,6]; 
A=[BS1;BS2;BS3;BS4]; 
number=300; 
pd0=0;
n=3; 
tt=5; 
% the number of RSSI measurement for each BS
for j=1:length(std_var)
    error1=0;
    error2=0; 
    std_var1=std_var(j); 
    for i=1:number 
        r1=A-ones(4,1)*MS; 
        r2=(sum(r1.^2,2)).^(1/2); 
        for k=1:tt 
            rssi(:,k)=pd0-10*n*log10(r2)-10^(std_var1/10)*randn(4,1); 
        end 
        RSSI1=mean(rssi,2);
        % ideal situation 
        r1=10.^((RSSI1-pd0)/(-10*n)); 
        % real situation 
        [p_est,n_est]=parameter_est(A,std_var1); 
        r2=10.^((RSSI1-p_est)/(-10*n_est)); 
        theta1=TOALLOP(A,r1,1); 
        theta2=TOALLOP(A,r2,1); 
        error1=error1+norm(MS-theta1)^2; 
        error2=error2+norm(MS-theta2)^2; 
    end 
    RMSE1(j)=(error1/number)^(1/2); 
    RMSE2(j)=(error2/number)^(1/2); 
end
% plot 
plot(std_var,RMSE1,'-O',std_var,RMSE2,'-s') 
xlabel('The standard deviation of RSS measurement (db)'); 
ylabel('RMSE'); 
legend('Ideal','Real');

仿真结果

寝室熄灯咯，睡觉睡觉！！！