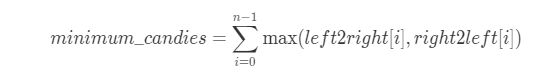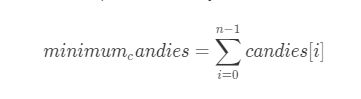流利说面试 & 用两个栈实现队列 & 237. 删除链表中的节点 & 119. 杨辉三角 II & 118. 杨辉三角 & 64. 最小路径和

 

 

 

面试官当时问我的是上面代码有问题没，我回答说会报错，又追问我是编译时报错还是运行时报错，我回答的是运行时会报错，又追问道回报什么类型的错误，我回答的是类型转换异常（因为map 调用get方法时，如果没获取到会返回值为null，把一个null类型的赋值给基本类型就会报错），然而经过现实运行，结果证明我的猜错是wrong。。。

135. 分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻的孩子中，评分高的孩子必须获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:

输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:

输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/candy

 

方法 1：暴力
算法

最简单的方法是使用一个一维的数组  candies 去记录给学生的糖果数。首先我们给每个学生 1 个糖果。然后我们开始从左到右扫描数组。对每一个学生，如果当前的评分 ratings[i] 比前一名学生的评分  ratings[i−1] 高，且 candies[i]<=candies[i−1] ，那么我们更新 candies[i] = candies[i-1] + 1 。这样，这两名学生之间的糖果分配目前是正确的。同样的，我们检查当前学生的评分 ratings[i] 是否比 ratings[i+1] 高，如果成立，我们同样更新 candies[i]=candies[i+1] + 1 。我们继续对 ratings 数组重复此步骤。如果在某次遍历中， candies 数组不再变化，意味着我们已经得到了最后的糖果分布，此时可以停止遍历。为了记录是否到达最终状态，我们用 flag 记录每次遍历是否有糖果数目变化，如果有，则为 True ，否则为 False 。

最终，我们可以把 candies 数组中所有糖果数目加起来，得到要求数目最少的糖果数。

作者：LeetCode
链接：https://leetcode-cn.com/problems/candy/solution/fen-fa-tang-guo-by-leetcode/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 

 public int candy(int[] ratings) {
	        int[] candies = new int[ratings.length];
	        Arrays.fill(candies, 1);
	        boolean flag = true;
	        int sum = 0;
	        while (flag) {
	            flag = false;
	            for (int i = 0; i < ratings.length; i++) {
	                if (i != ratings.length - 1 && 
	                		ratings[i] > ratings[i + 1] && candies[i] <= candies[i + 1]) {
	                    candies[i] = candies[i + 1] + 1;
	                    flag = true;
	                }
	                if (i > 0 && ratings[i] > ratings[i - 1] && candies[i] <= candies[i - 1]) {
	                    candies[i] = candies[i - 1] + 1;
	                    flag = true;
	                }
	            }
	        }
	        for (int candy : candies) {
	            sum += candy;
	        }
	        return sum;
	    }

方法 2：用两个数组
算法

在这种方法中，我们使用两个一维数组left2right 和right2left 。数组 left2right 用来存储每名学生只与左边邻居有关的所需糖果数。也就是假设规则为：如果一名学生评分比他左边学生高，那么他应该比他左边学生得到更多糖果。类似的，right2left数组用来保存只与右边邻居有关的所需糖果数。也就是假设规则为：如果一名学生评分比他右边学生高，那么他应该比他右边学生得到更多糖果。

首先，我们在left2rigth 和right2left 中，给每个学生 1 个糖果。然后，我们从左向右遍历整个数组，只要当前学生评分比他左邻居高，我们在 left2right数组中更新当前学生的糖果数 left2right[i] = left2right[i-1] + 1，这是因为在每次更新前，当前学生的糖果数一定小于等于他左邻居的糖果数。

在从左到右扫描后，我们用同样的方法从右到左只要当前学生的评分比他右边（第 (i+1)个）学生高，就更新 right2left[i]为 right2left[i] = right2left[i + 1] + 1。

现在，对于数组中第 i个学生，为了满足题中条件，我们需要给他 max(left2right[i],right2left[i]) 个糖果。因此，最后我们得到最少糖果数：

其中， n  是评分数组的长度。

作者：LeetCode
链接：https://leetcode-cn.com/problems/candy/solution/fen-fa-tang-guo-by-leetcode/
来源：力扣（LeetCode）
 

  public int candy1(int[] ratings) {
	        int sum = 0;
	        int[] left2right = new int[ratings.length];
	        int[] right2left = new int[ratings.length];
	        Arrays.fill(left2right, 1);
	        Arrays.fill(right2left, 1);
	        for (int i = 1; i < ratings.length; i++) {
	            if (ratings[i] > ratings[i - 1]) {
	                left2right[i] = left2right[i - 1] + 1;
	            }
	        }
	        for (int i = ratings.length - 2; i >= 0; i--) {
	            if (ratings[i] > ratings[i + 1]) {
	                right2left[i] = right2left[i + 1] + 1;
	            }
	        }
	        for (int i = 0; i < ratings.length; i++) {
	            sum += Math.max(left2right[i], right2left[i]);
	        }
	        return sum;
	    }

方法 3：使用一个数组
算法

在前面的方法中，我们使用了两个数组分别记录每一个学生与他左邻居和右邻居的关系，后来再将两个数组合并。在这里我们可以只用一个数组 candies ，记录当前学生被分配的糖果数。

首先我们给每个学生 1 个糖果，然后我们从左到右遍历并分配糖果，我们仅更新评分比左邻居高且糖果数小于等于左邻居的学生，将其更新为 candies[i] = candies[i-1] + 1  。在更新的过程中，我们不需要比较 candies[i] 和 candies[i - 1]  ，因为在更新前一定有 candies[i]≤candies[i−1] 。

从左到右遍历完后，我们同样地从右到左遍历。现在我们需要更新每个学生 i 同时满足左邻居和右邻居的关系。在这次遍历汇总，如果 ratings[i]>ratings[i + 1]  ，仅考虑右邻居规则的情况下，我们本应该更新为 candies[i] = candies[i + 1] + 1 ，但是这次我们仅当 candies[i]≤candies[i+1] 才更新。这是因为我们在从左到右遍历的时候已经修改过 candies 数组，所以  candies[i] 不一定小于等于 candies[i + 1]  。所以，如果 ratings[i]>ratings[i+1] ，我们更新为  candies[i]=max(candies[i],candies[i+1]+1]) ，这样 candies[i] 同时满足左邻居和右邻居的约束。

再一次，我们把 candies  数组中的所有元素求和，获得所需结果。

 

其中， n 是评分数组的长度。

  public int candy2(int[] ratings) {
	            int[] candies = new int[ratings.length];
	            Arrays.fill(candies, 1);
	            for (int i = 1; i < ratings.length; i++) {
	                if (ratings[i] > ratings[i - 1]) {
	                    candies[i] = candies[i - 1] + 1;
	                }
	            }
	            int sum = candies[ratings.length - 1];
	            for (int i = ratings.length - 2; i >= 0; i--) {
	                if (ratings[i] > ratings[i + 1]) {
	                    candies[i] = Math.max(candies[i], candies[i + 1] + 1);
	                }
	                sum += candies[i];
	            }
	            return sum;
	        }
	 

 

64. 最小路径和

 

概述
找出一条从左上角到右下角的路径，路径上数字之和最小。

题解
方法 1： 暴力
暴力就是利用递归，对于每个元素我们考虑两条路径，向右走和向下走，在这两条路径中挑选路径权值和较小的一个。 
cost(i,j)=grid[i][j]+min(cost(i+1,j),cost(i,j+1))

 

public class Solution {
    public int calculate(int[][] grid, int i, int j) {
        if (i == grid.length || j == grid[0].length) return Integer.MAX_VALUE;
        if (i == grid.length - 1 && j == grid[0].length - 1) return grid[i][j];
        return grid[i][j] + Math.min(calculate(grid, i + 1, j), calculate(grid, i, j + 1));
    }
    public int minPathSum(int[][] grid) {
        return calculate(grid, 0, 0);
    }
}
 

方法 2：二维动态规划
算法

我们新建一个额外的 dpdp 数组，与原矩阵大小相同。在这个矩阵中，dp(i, j)dp(i,j) 表示从坐标 (i, j)(i,j) 到右下角的最小路径权值。我们初始化右下角的 dpdp 值为对应的原矩阵值，然后去填整个矩阵，对于每个元素考虑移动到右边或者下面，因此获得最小路径和我们有如下递推公式： 

dp(i,j)=grid(i,j)+min(dp(i+1,j),dp(i,j+1))

注意边界情况。 

 

public class Solution {
    public int minPathSum(int[][] grid) {
        int[][] dp = new int[grid.length][grid[0].length];
        for (int i = grid.length - 1; i >= 0; i--) {
            for (int j = grid[0].length - 1; j >= 0; j--) {
                if(i == grid.length - 1 && j != grid[0].length - 1)
                    dp[i][j] = grid[i][j] +  dp[i][j + 1];
                else if(j == grid[0].length - 1 && i != grid.length - 1)
                    dp[i][j] = grid[i][j] + dp[i + 1][j];
                else if(j != grid[0].length - 1 && i != grid.length - 1)
                    dp[i][j] = grid[i][j] + Math.min(dp[i + 1][j], dp[i][j + 1]);
                else
                    dp[i][j] = grid[i][j];
            }
        }
        return dp[0][0];
    }
}
 

方法 3：一维动态规划
算法

在上个解法中，我们可以用一个一维数组来代替二维数组，dp 数组的大小和行大小相同。这是因为对于某个固定状态，只需要考虑下方和右侧的节点。首先初始化 dp 数组最后一个元素是右下角的元素值，然后我们向左移更新每个 dp(j) 为：
dp(j)=grid(i,j)+min(dp(j),dp(j+1))

我们对于每一行都重复这个过程，然后向上一行移动，计算完成后 dp(0) 就是最后的结果。

 

public class Solution {
   public int minPathSum(int[][] grid) {
       int[] dp = new int[grid[0].length];
       for (int i = grid.length - 1; i >= 0; i--) {
           for (int j = grid[0].length - 1; j >= 0; j--) {
               if(i == grid.length - 1 && j != grid[0].length - 1)
                   dp[j] = grid[i][j] +  dp[j + 1];
               else if(j == grid[0].length - 1 && i != grid.length - 1)
                   dp[j] = grid[i][j] + dp[j];
               else if(j != grid[0].length - 1 && i != grid.length - 1)
                   dp[j] = grid[i][j] + Math.min(dp[j], dp[j + 1]);
               else
                   dp[j] = grid[i][j];
           }
       }
       return dp[0];
   }
}

 

 

     
方法 4：动态规划（不需要额外存储空间）
算法

和方法 2 相同，惟一的区别是，不需要用额外的 dp  数组，而是在原数组上存储，这样就不需要额外的存储空间。递推公式如下：
 grid(i,j)=grid(i,j)+min(grid(i+1,j),grid(i,j+1))
 

public int minPathSum (int[][] grid) {
    for (int i = grid.length - 1; i >= 0; i--) {
        for (int j = grid[0].length - 1; j >= 0; j--) {
        	
            if(i == grid.length - 1 && j != grid[0].length - 1)
                grid[i][j] = grid[i][j] +  grid[i][j + 1];
            
            else if(j == grid[0].length - 1 && i != grid.length - 1)
                grid[i][j] = grid[i][j] + grid[i + 1][j];
            
            else if(j != grid[0].length - 1 && i != grid.length - 1)
                grid[i][j] = grid[i][j] + Math.min(grid[i + 1][j],grid[i][j + 1]);
        }
    }
    return grid[0][0];
}

 

 

763. 划分字母区间

package demo4;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Scanner;
//[LeetCode] 763. Partition Labels 分割标签
/*
 * 示例1:
输入:S = "ababcbacadefegdehijhklij"
输出(9、7、8):
解释:
分区是“ababcbaca”、“defegde”、“hijhklij”。
这是一个分区，因此每个字母最多出现在一个部分中。
像“ababcbacadefegde”、“hijhklij”这样的分区是不正确的，因为它将S分成更少的部分。
注意:
S的长度在[1,500]范围内。
S将只由小写字母('a'到'z')组成。
 */
public class Main3 {
	public static void main(String[] args) {
	    Scanner sc = new Scanner(System.in);
		String line = sc.nextLine();
		List list = partitionLabels(line);
		System.out.println(list.toString()); 
		
	}
 
	
	 public  static List partitionLabels(String S) {
			ArrayList list = new ArrayList<>();
			
			for (int i = 0; i < S.length(); ) {
				int find = find(S , S.charAt(i));
				list.add(find);
				i += find;
			}
			return list;
	}
	
	public  static int find (String str , char c){
		int indexOf = str.indexOf(c);//当前字符第一次出现的位置
		int indexOf2 = str.lastIndexOf(c);//当前字符最后一次出现的位置
		int i = indexOf +1;
		while(i < indexOf2){
			int index = str.lastIndexOf(str.charAt(i));
			if(index > indexOf2){
				indexOf2 = index;
			}else{
				i++;
			}
		}
		return indexOf2 - indexOf +1;
	}
	
}

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

import java.util.Stack;

public class Solution {
    Stack stack1 = new Stack();
    Stack stack2 = new Stack();
    
     public void push(int node) {
        
        stack1.push(node);
    }
    
    public int pop() {
    	if(stack2.empty()){
    		while(stack1.size()>0){
    			stack2.push(stack1.pop());
    		}
    	}
   
    	return stack2.pop();
    	
    }
}

237. 删除链表中的节点

请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点，你将只被给定要求被删除的节点。

现有一个链表 -- head = [4,5,1,9]，它可以表示为:

示例 1:

输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.
示例 2:

输入: head = [4,5,1,9], node = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.
 

说明:

链表至少包含两个节点。
链表中所有节点的值都是唯一的。
给定的节点为非末尾节点并且一定是链表中的一个有效节点。
不要从你的函数中返回任何结果。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/delete-node-in-a-linked-list

 

方法：与下一个节点交换
从链表里删除一个节点 node 的最常见方法是修改之前节点的 next 指针，使其指向之后的节点。

因为，我们无法访问我们想要删除的节点 之前 的节点，我们始终不能修改该节点的 next 指针。相反，我们必须将想要删除的节点的值替换为它后面节点中的值，然后删除它之后的节点。

因为我们知道要删除的节点不是列表的末尾，所以我们可以保证这种方法是可行的。

Java

作者：LeetCode
链接：https://leetcode-cn.com/problems/delete-node-in-a-linked-list/solution/shan-chu-lian-biao-zhong-de-jie-dian-by-leetcode/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public void deleteNode(ListNode node) {
        
        node.val = node.next.val;
        node.next = node.next.next;
    
    }
}

371. 两整数之和

不使用运算符 + 和 - ，计算两整数 a 、b 之和。

示例 1:

输入: a = 1, b = 2
输出: 3
示例 2:

输入: a = -2, b = 3
输出: 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sum-of-two-integers

题目说不能使用运算符 + 和 -，那么我们就要使用其他方式来替代这两个运算符的功能。

位运算中的加法
我们先来观察下位运算中的两数加法，其实来来回回就只有下面这四种：

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0（进位 1）
仔细一看，这可不就是相同位为 0，不同位为 1 的异或运算结果嘛~

异或和与运算操作
我们知道，在位运算操作中，异或的一个重要特性是无进位加法。我们来看一个例子：

a = 5 = 0101
b = 4 = 0100

a ^ b 如下：

0 1 0 1
0 1 0 0
-------
0 0 0 1
a ^ b 得到了一个无进位加法结果，如果要得到 a + b 的最终值，我们还要找到进位的数，把这二者相加。在位运算中，我们可以使用与操作获得进位：

a = 5 = 0101
b = 4 = 0100

a & b 如下：

0 1 0 1
0 1 0 0
-------
0 1 0 0
由计算结果可见，0100 并不是我们想要的进位，1 + 1 所获得的进位应该要放置在它的更高位，即左侧位上，因此我们还要把 0100 左移一位，才是我们所要的进位结果。

那么问题就容易了，总结一下：

1. a + b 的问题拆分为 (a 和 b 的无进位结果) + (a 和 b 的进位结果)
2. 无进位加法使用异或运算计算得出
3. 进位结果使用与运算和移位运算计算得出
4. 循环此过程，直到进位为 0

作者：jalan
链接：https://leetcode-cn.com/problems/sum-of-two-integers/solution/wei-yun-suan-xiang-jie-yi-ji-zai-python-zhong-xu-y/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution {
    public int getSum(int a, int b) {
    	int sum = a ^ b;
    	int ans = (a & b) << 1;

    	while(ans !=0){
    		int temp = sum;
    		sum = sum ^ ans;
    		
    		ans = (temp & ans) << 1;
    	}
    	return sum ;
    }
}

我的思路如下

class Solution {
    public int getSum(int a, int b) {
        
        while(b != 0){
        	a++;
        	b--;
        }
        return a;
    
    }
}

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

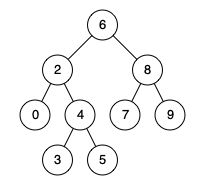
例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

 

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
 

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree

方法一 （递归）

算法

从根节点开始遍历树
如果节点 pp 和节点 qq 都在右子树上，那么以右孩子为根节点继续 1 的操作
如果节点 pp 和节点 qq 都在左子树上，那么以左孩子为根节点继续 1 的操作
如果条件 2 和条件 3 都不成立，这就意味着我们已经找到节 pp 和节点 qq 的 LCA 了

 

 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        // Value of current node or parent node.
        int parentVal = root.val;

        // Value of p
        int pVal = p.val;

        // Value of q;
        int qVal = q.val;

        if (pVal > parentVal && qVal > parentVal) {
            // If both p and q are greater than parent
            return lowestCommonAncestor(root.right, p, q);
        } else if (pVal < parentVal && qVal < parentVal) {
            // If both p and q are lesser than parent
            return lowestCommonAncestor(root.left, p, q);
        } else {
            // We have found the split point, i.e. the LCA node.
            return root;
        }
    }

方法二 （迭代）

算法

这个方法跟方法一很接近。唯一的不同是，我们用迭代的方式替代了递归来遍历整棵树。由于我们不需要回溯来找到 LCA 节点，所以我们是完全可以不利用栈或者是递归的。实际上这个问题本身就是可以迭代的，我们只需要找到分割点就可以了。这个分割点就是能让节点 pp 和节点 qq 不能在同一颗子树上的那个节点，或者是节点 pp 和节点 qq 中的一个，这种情况下其中一个节点是另一个节点的父亲节点。

 

 public TreeNode lowestCommonAncestor1(TreeNode root, TreeNode p, TreeNode q) { 
    	// Value of p
        int pVal = p.val;

        // Value of q;
        int qVal = q.val;

        // Start from the root node of the tree
        TreeNode node = root;

        // Traverse the tree
        while (node != null) {

            // Value of ancestor/parent node.
            int parentVal = node.val;

            if (pVal > parentVal && qVal > parentVal) {
                // If both p and q are greater than parent
                node = node.right;
            } else if (pVal < parentVal && qVal < parentVal) {
                // If both p and q are lesser than parent
                node = node.left;
            } else {
                // We have found the split point, i.e. the LCA node.
                return node;
            }
        }
        return null;
    }

 

118. 杨辉三角

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

class Solution {
    
    public List> generate(int numRows) {
         List> triangle = new ArrayList>();
      // First base case; if user requests zero rows, they get zero rows.
      if (numRows == 0) {
          return triangle;
      }
      // Second base case; first row is always [1].
      triangle.add(new ArrayList<>());
      triangle.get(0).add(1);

      for (int rowNum = 1; rowNum < numRows; rowNum++) {
          List row = new ArrayList<>();
          List prevRow = triangle.get(rowNum-1);
          // The first row element is always 1.
          row.add(1);
          // Each triangle element (other than the first and last of each row)
          // is equal to the sum of the elements above-and-to-the-left and
          // above-and-to-the-right.
          for (int j = 1; j < rowNum; j++) {
              row.add(prevRow.get(j-1) + prevRow.get(j));
          }
          // The last row element is always 1.
          row.add(1);
          triangle.add(row);
      }
      return triangle;
    }
    
    
}

 119. 杨辉三角 II

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

 

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

class Solution {
        public static  List getRow(int rowIndex) {
	        List result = new ArrayList<>();
	        if (rowIndex == 0) {
	            result.add(1);
	            return result;
	        }
	        if (rowIndex == 1) {
	            result.add(1);
	            result.add(1);
	            return result;
	        }

	        result.add(1);
	        result.add(1);

	        for (int i = 1; i < rowIndex; i++) {
	            result.add(1);
	            for (int j = 0; j < i; j++) {
	                result.add(result.get(0) + result.get(1));
	                result.remove(0);
	            }
	            result.add(1);
	            result.remove(0);
	        }

	        return result;


	    }
    }